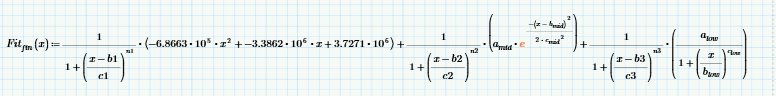Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
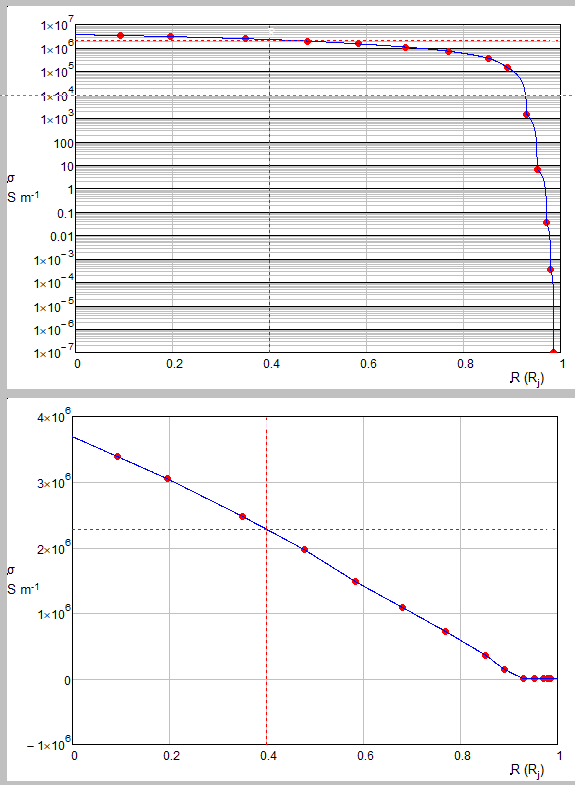
I need a formula for this points
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I need a formula for this points
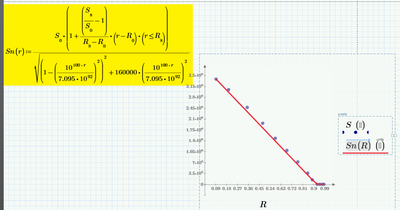
Can you show me one formula for this points? The Mathcad 15 sheet is in attach!
Thank you!
Solved! Go to Solution.
- Labels:
-
Statistics_Analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
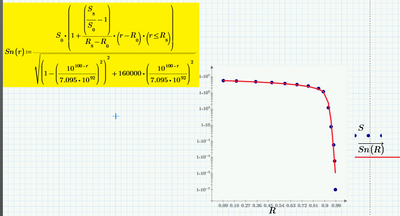
Look at the attached sheet.
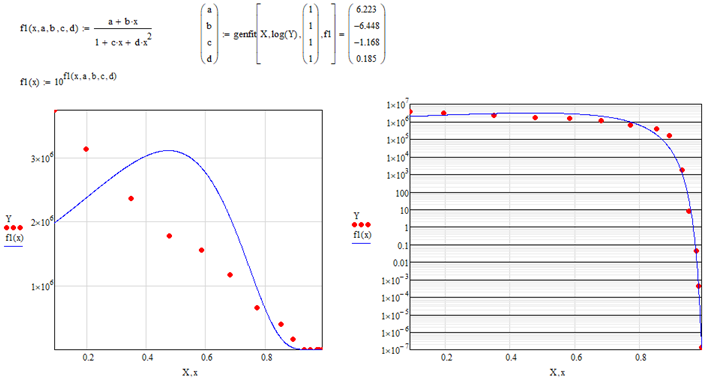
This RKD is nothing special - its an ordinary polynomial fit.
You could use polyfit as well! Same result!
It may be that d,k,b.i have special meanings in economics but we can happily get rid of them without altering the resulting curve.
And your observation concerning d and k seems correct. The economics play with 14 parameters for an 6th degree function while only 7 are necessary. So any change in one variable can easily be compensated by others.
As so often, economists invent high-sounding fancy names for quite basic elementary mathematics 😉
EDIT: changed sheet to show the polyfit gets the same result 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Yes - negative!\
Yes. DJF told you. Its a regression, not an interpolation.
The values are lower than the orginal data in the second half and as they are negative they don't show in a log-scaled plot. Is this problematic? Why?
Maybe it would help if you tell us what your exact need is.
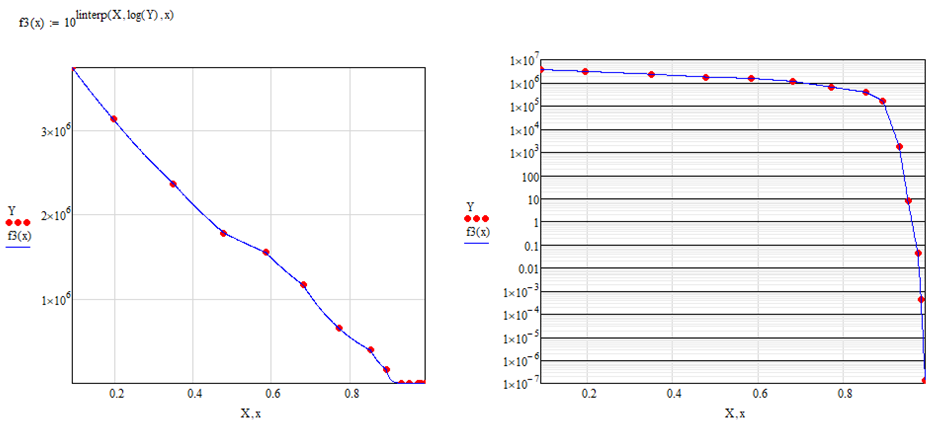
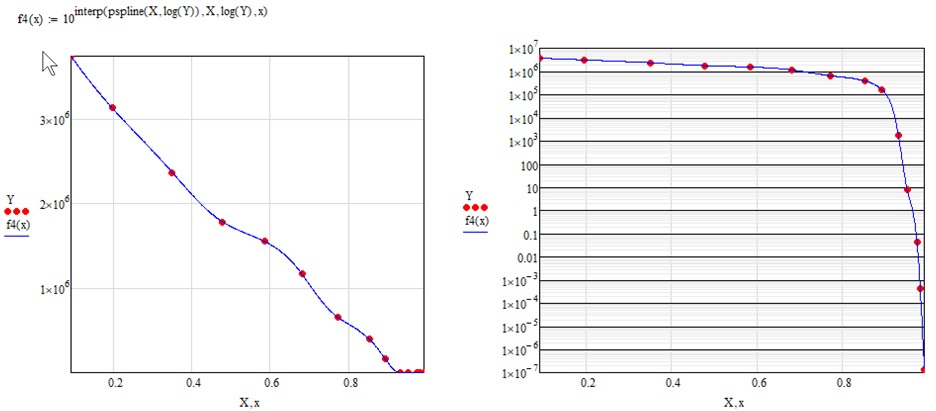
Why is linear interpolation of the original data not acceptable?
Whats wrong with linear or spline interpolation of the logarithmized data?
Whats the problem with Freds interesting approach?
>> The sheet please
Don't just look at pictures! Read the text of the posts and look at the attachments!
Fred had posted his sheet already long time ago -> https://community.ptc.com/t5/PTC-Mathcad/I-need-a-formula-for-this-points/m-p/581022/highlight/true#M183332
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In your initial post you show a plot with the y-axis log scaled. Is this what you need?
Then you have to be aware that the quite interesting solution of DJF will only give you what you need for the first part of your data, similar to what Terry had provided. You would need another function for the second part!
Guess you attached that log-scaled pic to show that you don't like that bumpy look when using linear interpolation, right?
So why not use linear interpolation of the logarithmized data. This should be easy enough to implement in C++ even though its not one single function equation.
You may also use splines, but I guess there's no benefit doing so and its quite a bit more work to implement in C++.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Can you show me one formula for this points?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
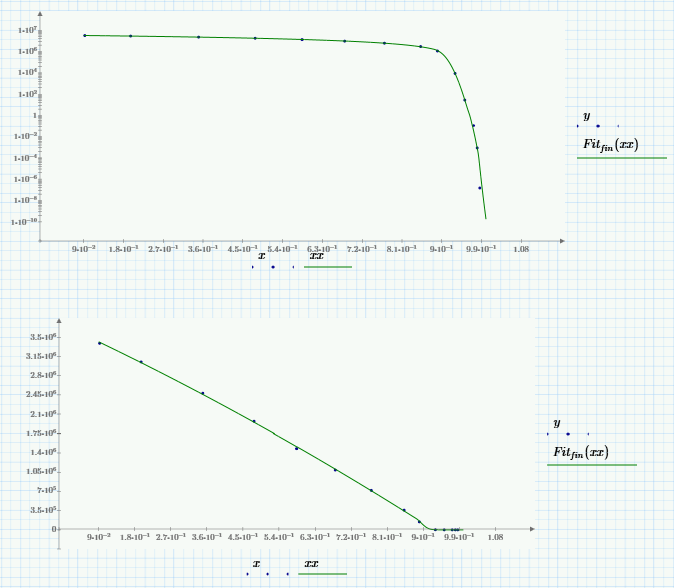
I felt we never got a great solution to this one so I've poked at it occasionally. Here's an approach that uses Butterworth filters to allow the combination of 3 unique curve fits. Still not perfect, but an interesting approach to have in your toolkit. The filters multiply the various fits by a square wave (~1 or 0) to turn them on or off as we progress along the X axis. In the end it's not much different than Fred's approach, but can help smooth the transitions.
4.0 attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I followed Fred's advise and got CurveExpert. It is ....ok. Works fine but a bit disappointing in the number of built-in equations it has. Continuing my search I then found http://zunzun.com/
It will brute force it's way through hundreds of equations, and it's free. I also contacted the site author and he made some fast updates for me. It didn't find a good solution to Valery's problem, but it's worth bookmarking. Bit confusing to use and slow, but seems very powerful.
Instructions:
Select 2D function finder
Paste in you data as text (into "text data editor" pull-down)
Continue to scroll through the various pull-down screens to select the options you want.
Hit submit (and wait a while, ~30 minutes if you're looking at all equations)
Equations come back ranked and plotted
- « Previous
-
- 1
- 2
- Next »