Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
I need help on how to solve this DIFEQ
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I need help on how to solve this DIFEQ
I'm trying to solve a set of differential equations, I removed the integral, but I don't know what exact information I'm missing. I'm getting the error message "you have too few equations".
Also, is it possible to make mathcad solve this using laplace method?
Thanks
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm not really an expert in Mathcad's numeric DE solvers, but I know this:
You want to find three functions of t: r1, r1 and q2. Then you need three independent expressions to describe them. Apart from the big one involving all three functions, you have two more in the Guess Values section. If you move them down to the Constraints section that might help.
Also I think you are lacking one more initial condition.
Regarding Laplace: the root is a big stumble-block here. While:
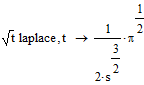
I see no way to find the Laplace tranform of:
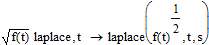 (Which basically tells you the laplace transform of sqrt(f(t)) is it's laplace transform...)
(Which basically tells you the laplace transform of sqrt(f(t)) is it's laplace transform...)
If you can get rid of the square roots that might help. But even then you end up with:
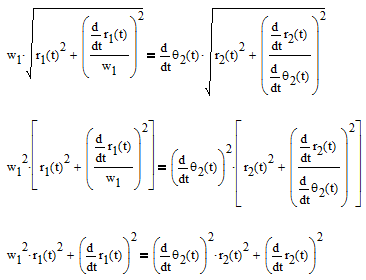
Where you multiply a function with itself, there too the laplace transform isn't readily available.
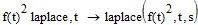
I know that convolution in the time domain is multiplication in the laplace domain:
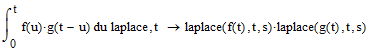
And I seem to remember that the reverse applies: Multiplication in the time domain is convolution in the laplace domain. But could not find the proof yet, maybe you can.
Edit note: That proof can not be found because the statement is not true. Multiplication in the time domain is NOT convolution in the laplace domain.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you manipulate the equations as Luc has done you will see you really only have one ODE, namely that for theta2. This is easily solved, analytically (because vrack(t) is just sin(t)) to find the solution given in the image below, assuming the initial condition is correct (the final condition is incompatible with the initial one).
Because r1+r2 = constant then (dr1/dt)^2 = (dr2/dt)^2 and these cancel (see Luc's equation above) to leave a simple expression for r1 and r2 that can be solved, in conjunction with r1+r2=constant, to get the expressions in the image below.
Alan






