Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Indefinite Integrals
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Indefinite Integrals
Hello community, I'm new to Mathcad so I need your help ![]()
I try to calculate indefinite integral but it doesn't work, maybe I'm doing this wrong way?

- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sometime Mathcad is a bit touchy and you have to be more precise:
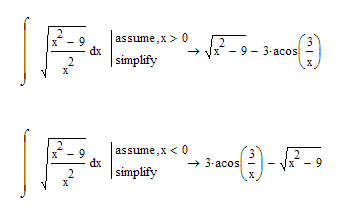
As you can see the results differs in sign depending on which part you'd like to integrate.
And sometime it sufficient to tell Mathcad that a variable is real only:
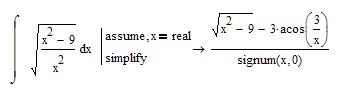
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmmm. Mathcad 11 gives this:
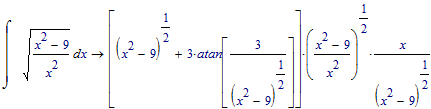
and simplification...:
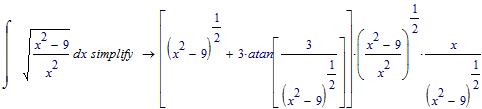
The same.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Further exploration:
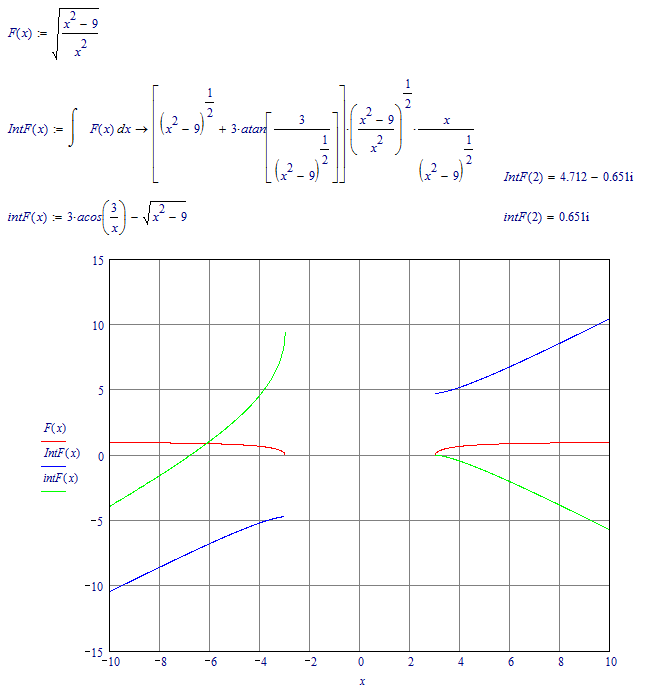
Quite a different result between Mupad and Maple!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As far as I know two integrals of the same function can be different only by a constant. So IntF(x) and intF(x) with different shapes, must have different derivatives...
But when differentiating the results:

I come back to the same F(x). Where's the mistake?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah, this looks more like it:
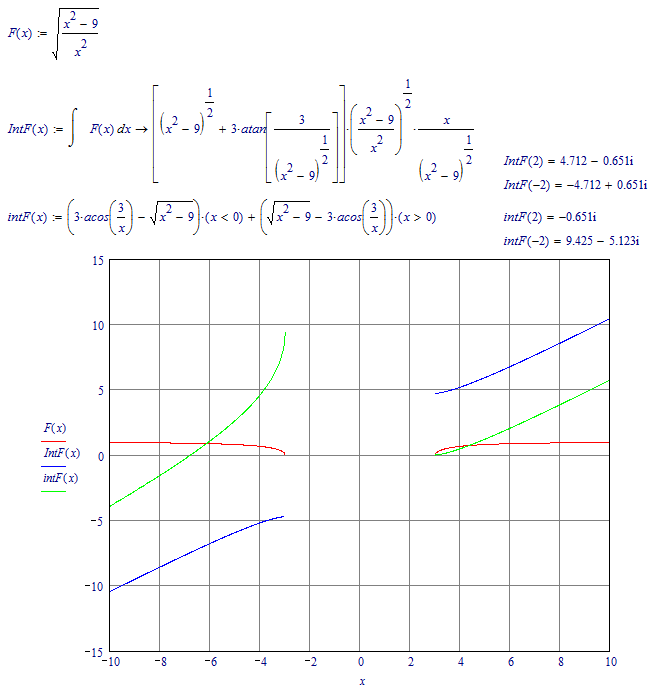
I guess Mupad goes wrong for x<0.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mystery (partly) solved:

That makes the (green) curve for far negative x going to -3 go to 3*pi, while for far positive going to 3 it goes to 0.
The result should have a signum with x in the acos as well:

Still the results of Maple and Mupad differ by more than a constant (because the constant changes sign with x).
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
better is if the signum is only the below root:

Now we're talking... But I like the Mathcad 11 (Maple) answer better, becaus it's more symmetric, like F(x) is.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Within a certain angle range we have asin(a) = atan(a/sqrt(1-a^2)) which explains the atan expression in the Maple result.
I am surprised that Maple does not simplify the factor
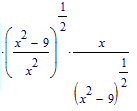
to sign(x), which in fact it is. After all as far as I reacall we don't have to tell Maple the we are dealing with reals - thats (in contrast to MuPad) automatically assumed.
The different domains of atan and asin also explain the vertical difference between the two solutions which, as I guess, is exactly 3*pi/2.
Mupads result seems to be wrong for negative x.
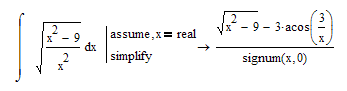
It rather should be
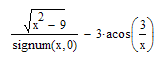
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Would you call that a bug?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes wrote:
Would you call that a bug?
Yes - guess its a bug.
Mathcad seems to know it:
Some further strange results:
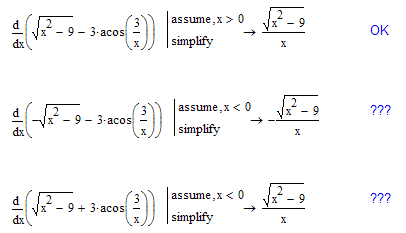
BTW, Wolfram Alpha agrees with Maple:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And I have some bad news for Prime 4 users:


Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Bad!
But better than a wrong result 😉
EDIT: I should have known it as its the same in Mathcad 15. We need to use "simplify" !
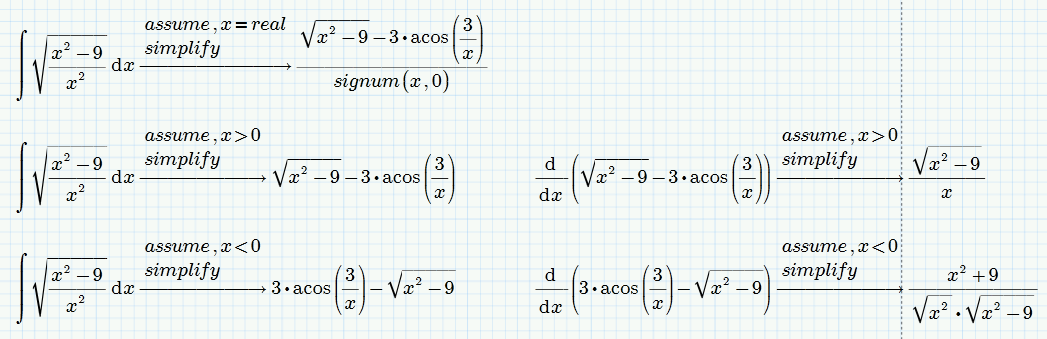
Here some other examples to demonstrate MuPads .... aehh .... capabilities.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime 4 didn't change with respect to that:

But I think it is weird, at least, that you would need a 'simplify' to make it remove the integral:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But I think it is weird, at least, that you would need a 'simplify' to make it remove the integral:
I won't call it weird - maybe just because I am used to it.
But ist quite OK to me that Mathcad does not make a simplification unless explicitly stated. In fact I would like to have much more control as to when an how Mathcads symbolics "simplify" an expression.
Same basic terms are automatically simplified by Mathcad, but just slightly more elaborate expressions need the command "simplify":
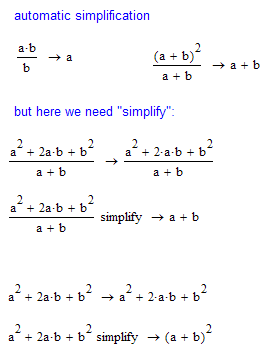
Is it different in MC11 with Maple?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is slightly different in Mathcad 11/Maple:

But I made my remark because I was surprised about the fact that a 'simplify' is required to evaluate an integral.
I would understand that the simplification of
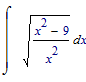 results in:
results in: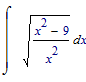
I would understand that the simplification of
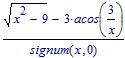 would result in
would result in 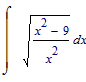
simply because the right part looks 'simpler' then the left one.
It makes no sense to me that when
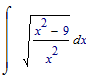 gives
gives  without simplification, it suddenly produces
without simplification, it suddenly produces 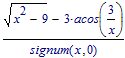 when simplification is called for.
when simplification is called for.
Anyway, I'm still very happy with Mathcad 11:
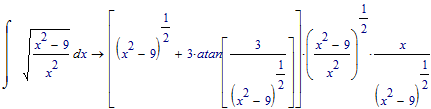
which 'simplifies to:'

(The same)
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maple (within Mathcad) does NOT automatically assume variables are real. Otherwise why would we have these symbolic keywords:
and the manual states:

Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm, "complex" was put at the modifier panel in Mathca 15.
I remember that Mathcad 14/15 often produce undesired results including expressions with the imaginary unit even though the result would simplify to a real if we assume all inputs are real. Whereas MC11 in the same case delivers a beautiful real result
And some expressions won't simplify fully in MC14/15 unless we assume that the inpunt vars are real where MC11 simplifies without having to assume that.
Remember some older threads about those effects.





