Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Infinite Series Convergence, how?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Infinite Series Convergence, how?
Hello,
I have attached my worksheet.
Is there a way for mathcad to tell me if an infinite series converges or diverges? And if it converges, what it converges to?
Thank you!!
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As ratio and root tests fail you have to use comparison to prove that this series converges (which does not mean that you now know what it converes to).
To evaluate that kind of series with Mathcad you have to use symbolic evaluation, not the numeric one you tried

Unfortunately Mathcads symbolics isn't capable to deal with your series. The results are different whether you force float mode (using 0.5) or exact mode (using 1/2), but not helpful in either case.
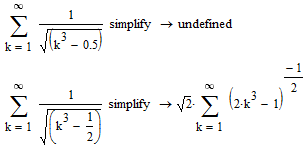
Mathcad is generally not really good with that kind of symbolics. While it knows about this series and successfully yields the Rieman Zeta as result
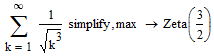
it isn't even able to deal with this (equivalent) series
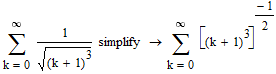
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for the help.
Can Matlab do this?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Can Matlab do this?
Matlab uses the very same symbolics processor (muPad, they own it), so I would guess - no. But if you have access, just give it a try.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Would it matter if I were able to tell MathCAD to compute the value within a specific accuracy?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
david h wrote:
Would it matter if I were able to tell MathCAD to compute the value within a specific accuracy?
No. Limiting precision can't help. You have an infinite series, so summing up "all" summand would take an infinite time. That means that Mathcad would have to find some kind of closed formula to be able to compute it and as it seems is not able to find one. BTW, if you write 0.5 Mathcads symbolics automatically(unfortunately) switch to float mode with limited precison (you could force it and control precision using the "float" modifier) and yields "undefined" as you have seen.
The numeric evaluation on the other hand is (for obvious reasons) not able to sum up to infinity and so fails if you put infinity as upper limit.
Best chances (if any) with Mathematica, maybe also Maple. You may also give the Wolfram Alpha webpage a try, who knows?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I believe that Fred's error criterion is incorrect, in that it stops the summation once the nth term is less than the input "error." However, there are still an infinite number of remaining terms, and the terms do not decrease rapidly enough to give a reasonable error bound based on the last term summed.(The last term does bound the error when the terms have decreasing magnitudes and the signs alternate - not the case here.)
The series converges, as can be easily shown. However, the actual error of a partial sum from the infinite summation is significantly larger than the magnitude of the last term summed.
The attached file has an approximation to the infinite sum within an arbitrary and calculable error bound (with the limits of the numeric calculation). I see the key to these types of problems as trying to manipulate the series so that only finite sums are needed in the approximations and the error bounds.
I find that the symbolic processor is not useful in leading the way to finding numeric bounds, as in this case, but it is useful to check the algebraic manipulations I wind up doing by hand.
Lou
P.S. I spent a lot more time on this than I would ever admit to, but I found the problem intriguing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Wow, impressive! Good job. You really spent some with that series 😉
And Mathcads symbolic agrees with your result:
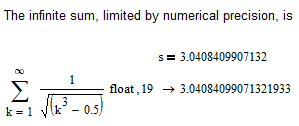
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I didn't think that the symbolic processor would calc a numeric result for an infinite sum. In MCD11 symbolics returns only the same original sum regardelss of the float value; doesn't attempt an evaluation. I tried the symbolic sum as you show in MCD15 and in Prime2, with your result in both cases. However, if the float limit is 20 or higher, then the symbolic answer is "undefined," in both versions, leading me to think that "19" did not appear in your evaluation by coincidence. Any idea why the boundary exists or what may cause it?
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Any idea why the boundary exists or what may cause it?
It is due to divine intervention. See some posts towards the end of this thread.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Lou Poulo wrote:
I didn't think that the symbolic processor would calc a numeric result for an infinite sum.
Its capable to do so in some cases - e.g. if we omit the "-0.5" we get Zeta(3/2) (as I posted here in another reply) as result which we could evaluate numerically using float. But for more complex series Mathcads symbolic has to resign.
However, if the float limit is 20 or higher, then the symbolic answer is "undefined," in both versions, leading me to think that "19" did not appear in your evaluation by coincidence. Any idea why the boundary exists or what may cause it?
Not the slightest idea. We discussed exactly that a bit below here http://communities.ptc.com/message/240162#240162
Its also not clear to me why using 0.5 and using the float keyword explicitely yield different results. I always thought that using a single decimal point in a symbolic evaluation has the same effect as using "float, 20" but for some reason beyond me there seems to be a difference.
Ooops, upon rereading my post it just dawnwd on me: decimal point IS float,20. Both would yield undefined.
In my prior post I compared 0.5 to float,10 and of course thats a difference. So one secret is disclosed 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The Maple engine in earlier versions of Mathcad can't deal with it either.
Also, this is what Wolfram Alpha comes up with:
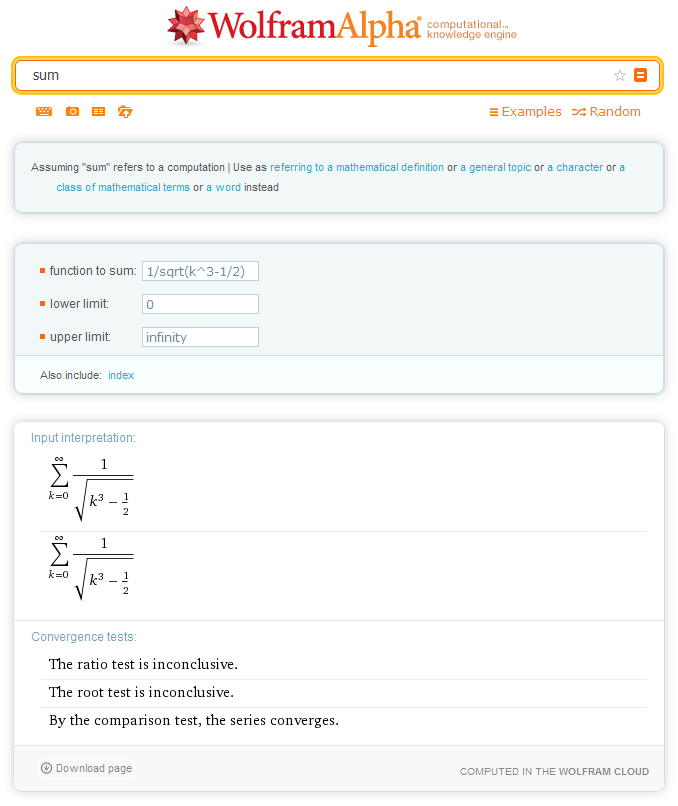
So I'm not sure Mathematica would give you an answer either.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good to know. I guess there will be no easy closed form of the limit. Have no acceess to Mathematica at the time here.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Can't insert pictures when editing the post above. 😞
I never tried this before, but it looks like Mathcad can at least tell us that the series is bounded above (lower bound 0 is obvious anyway); nte that this does not necessarily mean its convergent.
At least it works when we write 0.5, not with 1/2
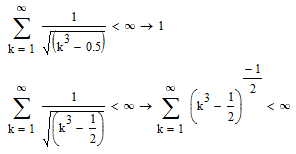
But there are two things I don't understand:
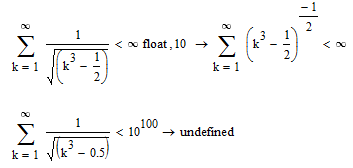
I always thought that using a decimal point in symbolic evaluation forces an automatic float, but obviously there is a difference
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I always thought that using a decimal point in symbolic evaluation forces an automatic float, but obviously there is a difference
That was also my understanding. So we just learned something, even if it's not what the sum converges to ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why don't you say from th every beginning you want to know what the sum converges to ![]() :
:
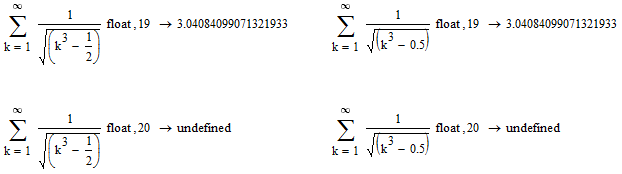
Will I ever understand that program (especially the symbolics)? ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
???????
Weird!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
???????
Weird!
Indeed! Symbolics sometimes is a miracle.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Quite!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I see you use the biblical Mathcad version 😉

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for everybody's help! You are very gracious for taking your time to help me. Hopefully someday I can help others as well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Trying to use the ratio test or the root test but they both not work.





