Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Integrals
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Integrals
It would be nice if the constant C is always equal to zero, because for some cases I have to take into account the particular value of this constant, or am I picking on too much?
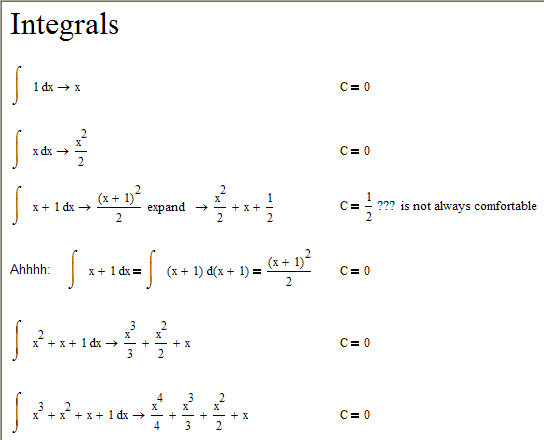
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Beginning calculus: Every indefinite integral has a constant term (since the derivative of a constant is zero) and there's no way to tell what it is. So the integrals above (without a constant term given) are assuming that the constant is zero (C = 0.)
Your individual problem needs to decide what C is equal to.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I understand, there are no mathematical errors, but
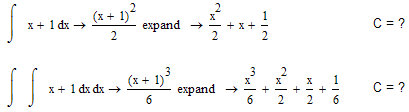
Is this my individual problem?
Fred Kohlhepp wrote:
So the integrals above (without a constant term given) are assuming that the constant is zero (C = 0.)
Are you sure?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I've tried to create a simple example, and ran into a constant of integration problem. See attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My example is much simpler than yours..., and yes, I agree, numerically there are no errors, but
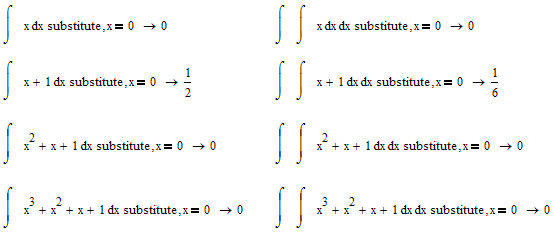
Do you understand me?
I think this is a bug, isn't it?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Universal User wrote:
I think this is a bug, isn't it?
I don't think it's a bug, unless the failure of the symbolic processor to insert a constant of integration is a bug.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So, trying to use Mathcad for solving my (not simple) technical problem I can not be sure that constant of integration C is ALWAYS equals ZERO, right???
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Universal User wrote:
So, trying to use Mathcad for solving my (not simple) technical problem I can not be sure that constant of integration C is ALWAYS equals ZERO, right???
NO. The integral (as Andy says below) is indefinite, the value of the constant must be determined from the context. (This is like the solution to a differential equation--there's a known form, but the values of the coefficients needs to be discovered by boundary/initial conditions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
While the answer that the symbolic processor gives is not incorrect (excuse double negative) it is misleading.
Result seems to indicate that the question is being re-defined to integral d(x+1) rather than dx (examples in attached).
And due to that, adds 1 (2) definite constant(s) into the answer(s) that should be indeterminate.
(Integral of x^2 + 1 gives a more "standard" answer)
Overall is it a bug? - probably.
regards
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I might be missing the question but:
An indefinite integral must have the constant added to the result, such as C1.
If, in the process of evaluation (probably a result of variable substitution) Mathcad provides a constant, It is not an error and it is not C1, it is (if you will) included in C1. As Fred says, the value of C1 is determined by boundary conditions.
If you want to integrate again, then add the C1 to the equation and drop the constant term
If you want a double integral, the collect the terms in x and replace with C2*x and the consant terms and replace with C1.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So what we decided? Symbolic notation does not match the displayed result when C equals to zero?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe I am missing the point, but it seems to me from your prior postings, that you assume, that every Integral has a "solution" running through (0/0) and you would like Mathcad to show you that "main"-Integral. At least thats what your setting x to zero implies. Think of INT(1/x,x)-->ln(x) - no way to apply your method.
I agree, that Mathcad ever so often simplifies Integrals not the same way I would do and Maple in Mathcad 11 did a better job. But one can argue if (x-3)^3 really is so bad compared with the polynomial expression without the constant 1.
What is the "right" result for INT(-2*sin(x)*cos(x),x)? -sin^2(x) or cos^2(x)?
Won't call it a bug but if you want to say that Mathcad is doing somethings wrong it could be its inability to explicitely give the constant of integration in its results.
As you seem to deal mainly with polynomial function, maybe substituting the indefinite integral for INT(f(t),t,0,x) will do the job better for you.
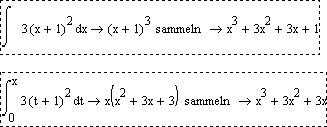
Regards
WR
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just feel the difference
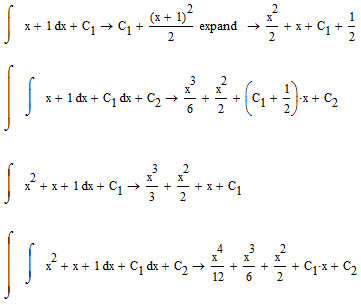
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Still, need to delete the 1/2 added to C1 it's just C1
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Think we understand your point.
The problem seems to be, that Mathcad does not have a decent mechanism to indicate the presence of an infinite number of solutions to a problem. If you let Mathcad solve the system of equations (x+y=3; 2x+2y=6) it yields the single solution (3; 0) and not something like (@1; 3-@1) where @1 could be any number. The solution (3; 0) is mathematically not really wrong, but heavily incomplete 😉
The same goes for indefinite integrals - Mathcad presents you with one function out of an infinite number you could choose from. There is no special kind of "variable/constant" it could use to indicate a (not the) constant of integration. Using an ordinary variable C1 Mathcad should not be allowed to sbstitute autonomous "C2" for "C1+3", e.g. If we would have a special kind of constants (but we dont have that in MC) build into Mathcad, it could substitute "@2" for "@1+3" like we learned in school.
Think we have to live with that limitation. If you really need it (what for?), as already written, in som ecases you could use the definite integral as shown.
WR

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I understand your point too... So, trust, but verify? ![]()
Here is an example:

For incorrect result substitute M=M1
So, you can solve this task numerically and you will get an incorrect result, right?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have been following the thread, and it seems as though you are trying to read more into the integration constant than is there. To my understanding, there is no unique C=0 case as you imply. In fact, the result you label as "Incorrect" in the most recent posted image I would say is just as valid as the "Correct" result. The deterministic way to say whether the indefinite integral result is valid is to differentiate with respect to x and see if you get the original integrand. This is true in both your "Incorrect" and "Correct" cases. As WR has pointed out, the "C" is determined only by applying an additional constraint, such as requiring that the result pass through (0,0). As he also points out, this doesn't work in the general case.
Lou





