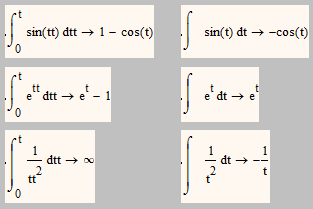Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Integration Error
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Integration Error
Dear Community:
I am user of MathCad 15. Integrate operation does not work. Integrate( t + a )dt answers 1/2( t + a )^2 instead of 1/2 t^2 + a t.
Shoud I install again MathCad?
Is it a known bug?
Where can I download patches?
Zeus.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for your help.
I found that, to make the initial conditions equal 0 or the additive constant equal 0, I must use definite integral from 0 to t in this case.
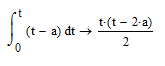
Which is the result, in a simple way, that I was looking for.
Thank you again.
Zeus
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Zeus Escudero wrote:
... Integrate( t + a )dt answers 1/2( t + a )^2 instead of 1/2 t^2 + a t.
...
1. What do you think you would get if you differentiated 1/2( t + a )^2 wrt t?
2. Indefinite integration is only defined up to an arbitrary constant (which Mathcad sets to zero).
3. Expand 1/2( t + a )^2? and compare with 1/2 t^2 + a t, bearing in mind comment number 2.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Alan:
The definite integral from 0 to t works ok. Are there options or preferences to force making the integration constant equals to 0? (as viewed 1/2 a^2 as inategration constant is so arbitrary).
Thanks
Zeus
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You could do the following:
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Alan:
In this example is easy to see the constant monomial, but, I am integrating large polinomials. I don't think this solution can be practical for a repetitive work.
In the other hand, Thank you for the idea to use definite integrals.
Zeus
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One problem is that there is no such thing as THE constant of integration - especially when the result can be written in different ways. Look at the next integral the result of which can be written in at least three different ways:
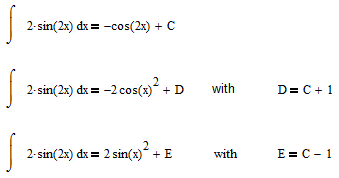
which constant of integration should Mathcad set to zero?
Of course Mathcad could default to eliminate any additive constant in the result regardless which way it may display it, but Mathcad isn't built that way (and sometimes I find that annoying, too).
This is what Mathcad does and at least one can say that the RHSs are ident
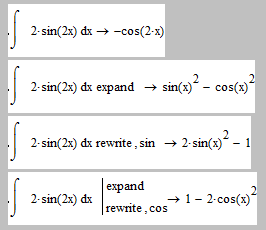
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for your help.
I found that, to make the initial conditions equal 0 or the additive constant equal 0, I must use definite integral from 0 to t in this case.
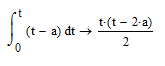
Which is the result, in a simple way, that I was looking for.
Thank you again.
Zeus
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well, fine if it works for the functions you are dealing with.
But keep in mind that this "method" will not get rid of all constants and may even add one.
Sometimes you may even get erranous results.
Furthermore I would suggest not using the same variable for integration and limit.