Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Integration calcul problem on Mathcad 14
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Integration calcul problem on Mathcad 14
Hi everyone,
I'm currently using Mathcad 14 and I think there is a problem in the software about the integration calcul.
I define a function as a density of probability, so its integral should be 1, but I don't get 1 with some certain bounds. In the picture I have enclosed to the question, you can see that when I integrate a normal law of parameters (μ=100,σ=1) on the interval [90,110], the result is 1. But when I integrate the same function on the interval [0,∞[, the result is 0.
Does anyone has already faced this problem ? Do you know if there is a patch to correct this mistake ?
TIA for your answers guys.
Yvan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad 11:

I can understand that the numerical integration from 0 to infinity gives a 0 result, because the numerical integrator might take big steps and miss the narrow peak at x=100.
You can see that if you split the integration into two, one from 0 to 100 and the other from 100 to infinity would give you the desired 1. Also with a less drastic upper limit, 200 instead of infinity, gives 1.
But the symbolic processor should not be fooled, so I was surprised by two answers. The symbolic integration of 0 to infinity, until I realised that adding the = again calls for numeric solution.
The other is the integral of 100 to infinity. Apparently the symbolic processor really doesn't know the dnorm function.
So, numeric integration of the the function alpha from 0 to infinity gives 0 is not a bug. You should investigate your function and if it is weirdly shaped, like alpha,
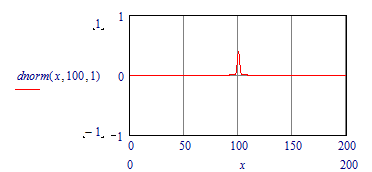
you should expect weird answers.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
See how the answers change if you learn dnorm() to the symbolic processor:
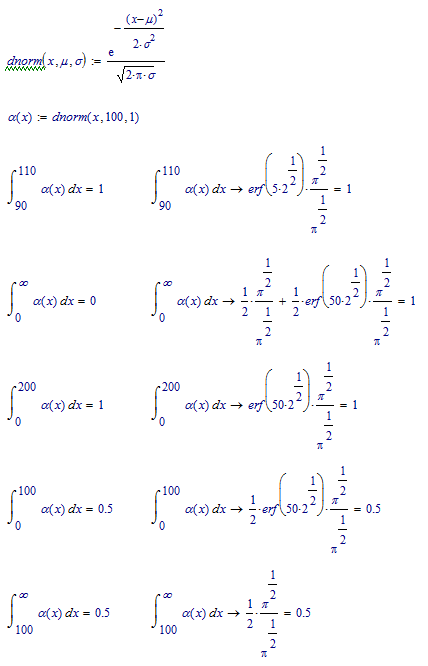
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> I define a function as a density of probability, so its integral should be 1
Not exactly - it should be exactly 1 if the lower limit is -infinity. With your lower limit of 0 you miss approx 1.3*10^2174 ![]()
As Luc already explained its a numerical issue, not a bug.
For numerical integration the interval from lower to upper bound is divided into a number of segments where the function is evaluated.
"infinity" for the numeric processor is 10^307.
I dont know the exact algorithm used by Mathcad but chances are, the intervals this huge range is diviided into are that big, the no function value is significantly over 0.
Mathcads numerics should simply refuse to evaluate improper integrals with limits +-infinity but obviously it doesn't.
You can influence the outcome by changing the value of the system variable TOL, but of course no value of TOL would give you the desired result for a limit infinity (10^307).

Normally the advice would be to evaluate improper integrals only with Mathcads symbolics, but in this case its not possible as the symbolics is not aware of the dnorm function.
Only way round I see is to define the function for the normal distribution yourself (DNorm in my example) and evaluate symbolically:
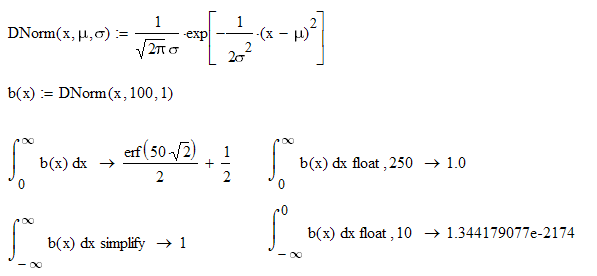
EDIT: Ahh ! Luc was faster with his second reply
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot Luc and Werner for your very clear answers, I now understand why those results are like that but I still find it ... strange !
The problem is that I found that "problem" because I was intended to code a function who generate the pdf from the sum of 2 continuous variables.
You may know that you can calculate this pdf with the convolution product of your variables, so I code this but it didn't work so much.

When the 2 distributions are close ( I mean that their graphic representation had some commun points ), you've got almost a pdf ( integral of μ=0.994).
But, as soon as you change one pdf, it goes wild !

I also find this :

So, do you think I had to exprimate my bounds in function of the mean and the variances of my pdf ? I don't have any other ideas ...
Thanks again Luc and Werner.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Who is "dnorm1" (or "dnorml") that you use to define the beta's?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Still you have to be very careful with your numeric integration. Watch what happens if you swap the functions alpha and beta:

Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But if you do the exercise properly and symbolically you get:

Which demonstrates that it does not matter if you swap the two functions in the convolution, as it should.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When you define alpha(x):=dnorm(x,10,1), alpha is the pdf from a normal law with (10,1) parameters.
dnorml is for a log-normal law.
Yes you're right, and the integral of alpha is less than 1 but it's supposed to be a pdf.
Thank you Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Log-Normal distribution
Mathcad (at least... the English language version) knows the pdf of this distribution as dlnorm (rather than dnorml ).
Do you have a French language version where it is dnorml, or did you define it yourself ?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Okay.
Yes, in my version it's dnorml.
So what I have done is to calculate my bounds in function of the mean and the variance of my pdf, in order to integrate on the part where the density is the biggest.
Yvan





