Hello, Everyone.
Is there a bug in the following: (1),(2), or (3) ?
Thanks in advance for your time and help.
Regards.
ACCEPTED SOLUTION
Accepted Solutions
Believe me
The "problem" is Mathcad chosing an "arbitrary" solution from an infinite number of (correct) solutions.
That way your second equation does not simplify to zero for every value of x.
That way, associative law does not apply.
You should not get 0 when simplifying your equation (2) as we have a single value at the left and an infinite number of values at the right, one of them happens to be the left one. Its the same situation as in your equation (3) but for some reason MuPad now realizes the difference.
Maybe you understand the "thinking" of Mathcad better that way:
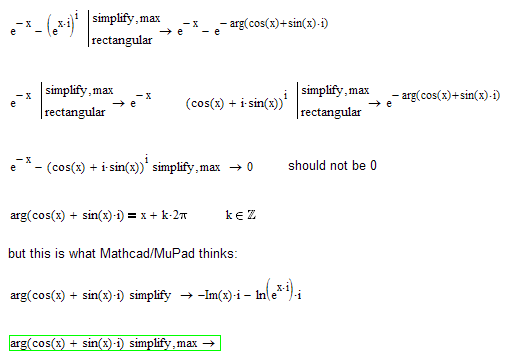
I didn't wait for simplify.max to finish.
WE
We already had this discussion quite a while ago.
The reason was and still is that mathematical laws are not the same for real and complex numbers.
(e^(5i))^i is NOT e^(-5) as you expect. At least not alone. (e^(5i))^i = e^(i*(-5+k*2 pi)) with k being any integer.
Mathcad/muPad is aware of this only in part.
Mathcad choses one of these possibilities and it happens not to be the one with k=0 but it happens to be the one with k=1 (for whatever reason).
Facit: You have to be more careful, when dealing with complex numbers, complex identities and should not assume, that rules, which are valid in R (real numbers) are also valid in C (complex numbers), too. Mathcad/muPad is not fully aware of all ambiguities which you encounter, when dealing with complex numbers. And it looks like Maple in Mathcad 11 is always applying rules from real to complex, which may be convenient, but mathematically not correct.
Calculating with complex numbers is more complex (sic!) than you might expect at first glance. Mathcad is not a suitable tool to explore that area.
Werner
.PNG)
Believe me
The "problem" is Mathcad chosing an "arbitrary" solution from an infinite number of (correct) solutions.
That way your second equation does not simplify to zero for every value of x.
That way, associative law does not apply.
You should not get 0 when simplifying your equation (2) as we have a single value at the left and an infinite number of values at the right, one of them happens to be the left one. Its the same situation as in your equation (3) but for some reason MuPad now realizes the difference.
Maybe you understand the "thinking" of Mathcad better that way:
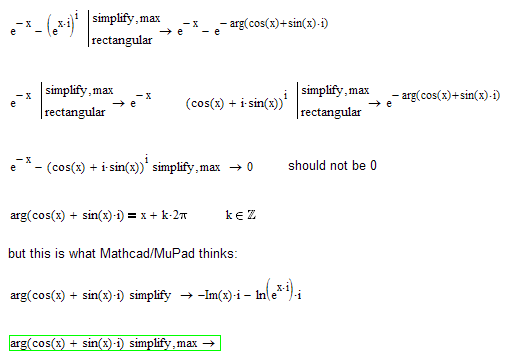
I didn't wait for simplify.max to finish.
WE
.PNG)
I also guess so. I totally believe that.
Thanks and thanks...again. I greatly appreciate your time and help, again, Werner. 
Best Regards.
Loi.
