Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Laplace Transform of integral
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Laplace Transform of integral
I got some homework to do and cant figure out how to solve an equation.
I have an idea but I'm not sure if I can do it the way I want.
As you can see in the document my problem is that the formula I use has f(t)dt in the integer but the equation I have to solve uses tau in in the integer but it wants me to take the integer from 0 to t.
I don't feel like i explained the problem very well but it should be easier to understand if you read through the document.
There might be other errors in the document but I have been wrestling with that part of the problem for what feels like hours now so I just finished it and threw it up here for you to have a look at.
Anton
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Tay is a dummy variable, this is, some letter but can be any other. The primitive (this is, the integral transformation, not just a number, a function) of y(tau)dtau must to be applied following Barrow rule, this is, substracting the values from the end to the initial point. So, tay dissapear, and the integral is well writed.
In the attached the solution. See the tables for the laplace transform properties to see how it applies to a derivative and to an integral. In mathcad 11 it can be automated to handle the entire process in only one function, but in mathcad 14 is ... better use copy, paste and editing.
Regards. Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It might be as simple as that. I didn't read the document, only your work sheet. The way the integral is shown is for continuous plotting . But in term of the numerical evaluation it is done between limits, between o and and the "end" in the Odesolve as well. That's my interpretation but wait more collabs agree on that interpretation.
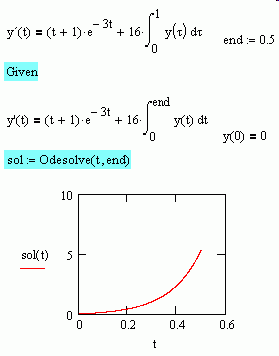
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What I meant by document was Worksheet![]()
I dont think this is the answer I need, since i cant solve it numericaly. I would have no problem solving this equation if all the varibales had a value ![]() or if i had to find the laplace for the integer between 0 and t for y(t)*d*t
or if i had to find the laplace for the integer between 0 and t for y(t)*d*t
But how would you find the laplace for the integer between 0 and t for y(tau)*d*tau. I cant find any examples thatt are simmilar, and I cant find any thing in my notes that help me here...
I am beginning to think that it could be typing error on my teachers behalf.
Anton
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Tay is a dummy variable, this is, some letter but can be any other. The primitive (this is, the integral transformation, not just a number, a function) of y(tau)dtau must to be applied following Barrow rule, this is, substracting the values from the end to the initial point. So, tay dissapear, and the integral is well writed.
In the attached the solution. See the tables for the laplace transform properties to see how it applies to a derivative and to an integral. In mathcad 11 it can be automated to handle the entire process in only one function, but in mathcad 14 is ... better use copy, paste and editing.
Regards. Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you
I looks about right. I got the same solution in another worksheet.
I'll find out if it is correct tomorrow
Anton
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alvaro,
Your approach is not solvable toward an explicit solution. Your Laplace is undetermined naturally and incorrect in the sense of the next DE solver. The problem is not ill posed but "quizly posed" wrt the integrand. The integrand is not a function and will therefore have only a numerical running solution . The integrand and the differential operator is correct but these representation is only to isolate the solution for the running limit, which limit maybe simply linear or any nonlinear function itself. But for the case it is a member of a DE. the upper limit is the "end" of the DE . This type of homework quiz is typical of a "Mathcad classroom" It may have to be entered much differently in other CAS.
The other point is what is the point to transform something in the Laplace domain if no Laplace algebra is applied, good question indeed ! That problem reminds me the Melanie Turenne ITER DE. It was like abandoned though I had given the final Odesolve. About the ITER solution, it is obvious that there was a discontinuity in the solution and the final solution exhibits this discontinuity about the voltage surge in the cabling system, surge under opening the circuit. The discontinuity is in literature "courant de rupture" on what the breakers are designed wrt the energy it is desired to protect the grid.
Cheers Alvaro & collabs: Jean
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
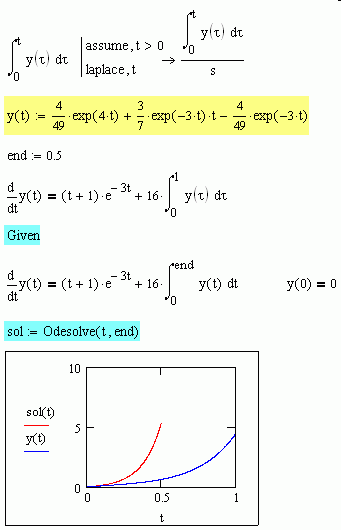
The proposed symbolic soltion verify the original equation. By theorems of unicity, given that a solution is proposed (even can be determined if it exists, is hard to handle, needs Lipschitz conditions or other hardest, and are not easy to prove) the solution is also unique. For this read the Check label in the file submited.
The correct interpretation for a definite integral as a function of the upper parameter is the given also. Notice that a "definite integral" is a real number, but a "primitive" is a function, or more preciselly, a familly of functions, if you take in consideration de usual "integration constant" C.
To avoid problems in the interpretations is why the integral parameter (tau in our case) is used, and not the upper limit (t). This is, a dummy variable (variable muda in spanish)
The proposed equation isn't an ODE. Is an integrodiferencial -in spanish- equation, and have a lot of common applications, not just for classroom.
In your gif, or the t in the upper limit of the integral isn't the same as the argument of laplace, or is a bug in mcad11. The property to apply is:
laplace(int(y(tau),tau=0..t),t,s) = laplace(y(t),t,s)/s
Check laplace tables for it.
In the attached the symbolic and the numerical soltuions, and the plots, showing that are basically the same.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Tanks Alvaro,
Nice explanation and setup.
It would be interesting to put it in the Laplace DE solver.
RemToDo for spare time .
Jean
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You explanation and the one i got from my teacher to day was almost the same. So my big "problem" was that I didn't understand the function of t and tau but hey I got it done.
for your wieving pleasures here is the final woorksheet. Did it manualy too just get the traning.
Anton
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Anton Jelle wrote:
You explanation and the one i got from my teacher to day was almost the same. So my big "problem" was that I didn't understand the function of t and tau but hey I got it done.
for your wieving pleasures here is the final woorksheet. Did it manualy too just get the traning.
Anton
A more formal solution is needed. What you got is intuitively not correct.
jmG
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Collab,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Primitive:
http://en.wikipedia.org/wiki/Antiderivative
Notice that, as operator, the primitivization operates over the domain of functions returning family of functions. The definite integral operate over functions but returns reals. So: are very very distinct concepts.
With primitives (Ctrl+I in mathcad) you must (or it is usual) use the correct letter inside the integrand, and in the differential. But with definite integrals, where you obtain reals numbers (the complex integral is another distinct animal) the letter inside the integral can be any other. If you want some kind of function, the usual way to obtain it is making variable the upper integral limit. For derivating this must to apply
http://en.wikipedia.org/wiki/Leibniz_integral_rule#Variable_limits_form
Technically -or historically, or who knows why- we prefer use not the same letter, and use a dummy variable, when it don't run outside of an operator, like in sums or others. You can read who it can confuse experimented programs in a bug report in mathcad 14 preciselly because it can take the same variable name in the upper limit and in the differential (old maple kernel reject this constructions):
http://collab.mathsoft.com/read?122135,99e#122135
To read examples about this kind of equations -i don't know english references- in spanish:
Ecuación íntegro diferencial, page 491, example 5, the "main orinigin", a RLC circuit:
solved by laplace, can transform it in any other model, by equivalents (mechanic, hidraulic, thermic, etc). Because it is why i say that it is very common situation in engineering.
Another reference: page 134 in
Can find more searching inside books with google.
Jean: the solution obtained is correct, just because it check the original equation and we know for some theorems that there are a solution. In the attached, a full numerical solution is developed also.
Regards. Alvaro.
PS: 1. In the vertical implies, you forgot the equal sign. You can isolate (equating to zero in this case) or not. Definite Integrals, integrals transforms and other operators can be applied to both sign of the equality. Isn't the case for derivatives or primitives, where you lose or gain a constant.
2. I see that you correctly use Phi(t) to well define y(t).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Interesting Alvaro,
Will look at it again, not today.
I'm promised a sunny Saturday.
Jean
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Anton, Alvaro,
Nothing has changed, the solver is totally correct in two lines of code. The route to the solver is a long story in the former Akiva collab. It comes out from Mathcad Maple 11.2a but I have not conserved the construct once proved and tested. In case Mathcad 14/15/Prime does not like the solver, here is also the image. The notation given by the "Professor" in cause and in quiz is incorrect. It is correct in the sense that the construct would arrive at the same result via the step function [f] integrated over Dirac D(t). The result is the same to the solver, but like giving the alphabet to explain a word or if you prefer: skinning the cat with a robot instead of by hands. If you want an export, evaluate the compacted red instruction, copy or "transport" the RHS of the symbolic evaluation. That will make the given DE work in low software like Excel and subjected to the project conditions.
There is lot less theory in books for Engineers than in the web for distraction.
Projects need what make them work and produce.
Cheers, Jean
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A nice project that was missing for the tool box.
Done Mathcad 11.2a , no red except intentional
for the symbolic compactor. Hope it works in
versions 14/15/Prime.
Thanks Alvaro for your input.
Jean





