Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Looking for Excel limitations
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Looking for Excel limitations
Many years ago as a young(er) engineer I received a memo (from someone who may happen to be a regular contributor here) about the dangers of spreadsheets. One of the key points was the mathematical limitations of excel - in the memo demonstrated by a Runge-Kutta solution not being accurate. I have a few questions may be you can help me with:
a.) Have there been any upgrades to Excel in the last decade that corrected such issues?
b.) Does anyone happen to have an example that shows bad excel results vs mathcad/matlab/maple etc. (Limited time for me to attempt to reproduce the R-K at the moment)
c.) Any other examples or reasons on why excel is probably not the best choice for engineering calculations? (besides clarity and operation order)
Thanks,
- Labels:
-
Mathcad Usage
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Both Mathcad and Excel make it easy to generate numerical results with floating point error. For example, try calculating 1/(0.3-0.1-0.1-0.1) in Mathcad and Excel (you'll get a surprising result).
You need a full computer algebra system (like Maple) if you want truly numerically accurate results
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
c.) Any other examples or reasons on why excel is probably not the best choice for engineering calculations? (besides clarity and operation order)
When it come to Mathcad its ability to be able to deal with units sure is a huge plus!
When it comes to numerical accuracy I wouldn't expect any big differences as both use the IEEE format for that.
But Mathcad may have better and more stable numerical algorithms implemented (not sure about this as I never would use Excel for any scientific or engineering calculations) and in Mathcad you have the option to use its symbolic calculations as well (even thought they can't compete with Maple or Mathematica).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Without having access to the actual implementations of both the Excel and the Mathcad RK routines it will be hard to pinpoint what went wrong, and whether updates (may) have resolved it.
As far as I can tell, given the same sequence of calculations, both Mathcad (11) and Excel (2007) give the same results.
Well, there's no symbolic in Excel. So numerics only:
All this to demonstrate that to implement a numerical (approximation) algorithm requires careful attention when big and small numbers are both into play...
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
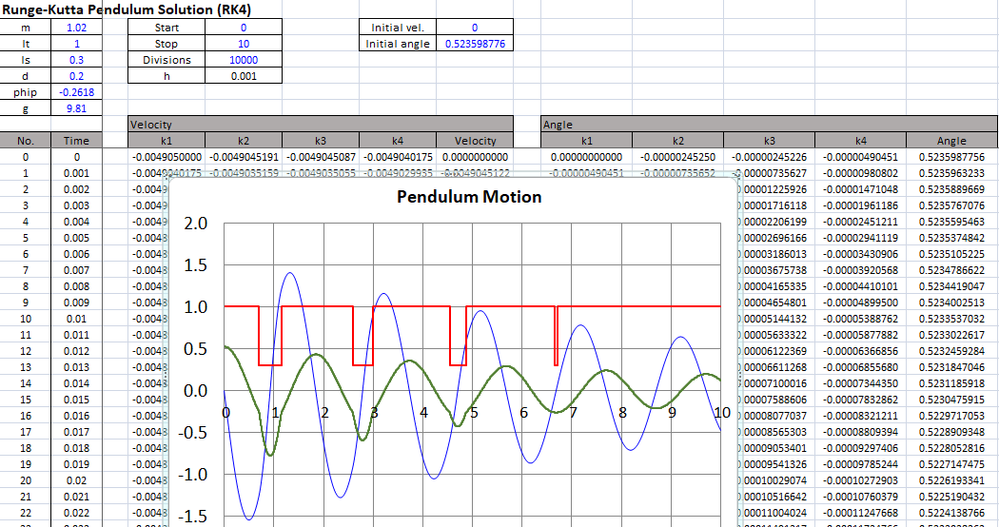
Did some work on this and seemed to confirm the issue that was I was told existed in Excel.
Here is some background to the problem (minus any mention of excel):
https://community.ptc.com/t5/PTC-Mathcad/Pin-and-Pendulum/td-p/332104
In the attached I used an RK4 routine in mathcad (4.0) and then duplicated that in Excel. (avoiding built-in functions to be apples-to-apples) Sure enough, in Excel I only see that the pendulum strikes the pin 3 times. I need to bump the division count up to ~12000 to observe the 4th strike in excel.
So, that's interesting. I'm curious if anyone seems a flaw in the analysis or has a good explanation for why different results are obtained between two programs.
Thanks,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One observation already:
The Prime implementation uses a definition of f(x,u) which internally does not refer to x.
So it could be better/as well a function of one parameter. f(u).
Changed it, and it does not make a noticable difference..
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Found it!
That happens when you implement the functions differently.
The problem essentially lies with the function to calculate the length of the rope to be used.
In Prime the function l(phi) is called from within the function f, using the angle calculated for each k (k1...k4) as it is input to f. In contrast in Excel, the angle used to determine the length is the same for every k.
So once corrected:
Conclusion: (As Werner noted) there's no (major) difference in accuracy between Mathcad and Excel.
(I hope I didn't ruin your case for Mathcad and against Excel.)
Success!
Luc