Community Tip - Visit the PTCooler (the community lounge) to get to know your fellow community members and check out some of Dale's Friday Humor posts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
MC doing wrong squaring a vector?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
MC doing wrong squaring a vector?
I'm not sure, but if X is a vector, shouldn't X^2 give the same result as X*X?
I think Mathcad is doing wrong here, as squaring should be interpreted as scalar product.
The vector with each element squared I would only expect as a result when I use vectorize.
Or am i missing the point?
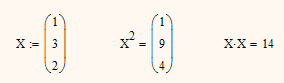
BTW, the effect is the same in MC15 and Prime2.
- Labels:
-
Physics
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you vectorize X*X you match x^2
Isn't a dot product suppose to provide a scalar?
Norm
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Isn't a dot product suppose to provide a scalar?
Yes, thats exactly what I was talking about. I'd expect to be X^2 a scalar, too.
In my opinion itt should only be the vectorization which applies the operation singly to each element.
X^(-1) should return an error, if X is not a square matrix, etc.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When X is a column vector, then X*X should return an error if Mathcad were complying with the normal rules of vector multiplication. However, all versions of Mathcad I'm aware of (going back to 3) have deliberately chosen to treat X*X as though it were the transpose of X (ie a row vector) multiplied by X, and have chosen to implement X^2 as an element by element operation. These are not strictly errors, but choices (poor choices possibly, but deliberate!).
If you let X be a non-square matrix (rather than a single-column vector) you get the expected error message for both X*X and X^2.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your explanations, Allan.
In one point I don't agree. Let X be a column vector, so X^T*X (interpreted as a matrix product) should (it doesn't in MC) return a 1x1 matrix, while the scalar product X*X is supposed to return a scalar.
It's OK that Mathcad does not provide different operators for matrix product and dot product (while it could) and defaults to dot (scalar) product in the case of X*X.
The surprising part for me was that automatic vectorizing and therefore the difference between X*X and X^2. But I could image that its more convenient in some situations to have that auto vectorizing done rather than being confronted with an error.
Funny I didn't stumbled upon this much sooner. Maybe I did and haven't thought enough about it.
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Thanks for your explanations, Allan.
In one point I don't agree. Let X be a column vector, so X^T*X (interpreted as a matrix product) should (it doesn't in MC) return a 1x1 matrix, while the scalar product X*X is supposed to return a scalar.
Werner
Yes; for consistency, X^T*X should be a 1x1 matrix, which, in Mathcad, is different from a scalar (personally, I prefer to think of a 1x1 matrix as a scalar!).
I guess Mathcad takes the approach it does here because it doesn't consider row vectors to be true vectors (most "vector" operators in Mathcad don't work on row vectors). Coming from a Matlab background I find this annoying - but I've learned to live with it over the years!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes; for consistency, X^T*X should be a 1x1 matrix, which, in Mathcad, is different from a scalar (personally, I prefer to think of a 1x1 matrix as a scalar!).
I guess Mathcad takes the approach it does here because it doesn't consider row vectors to be true vectors (most "vector" operators in Mathcad don't work on row vectors). Coming from a Matlab background I find this annoying - but I've learned to live with it over the years!
Yes Alan (sorry for the double "l" in the last post), I agree and usually consider a 1x1 matrix a scalar myself, too. Just was doing some hair splitting 😉
The inability of MC to accept row vectors is annoying but usually can be worked around using transpose quite well.
Wonder if Prime will be doing better in that respect - at least we sem to be able to extract rows equally easy from matrices as columns now.
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A dot product is a well known and defined operator, and the result is a scalar. As far as I know, there is no particular definition for the square of a vector (and certainly not that it should be the same as the dot product), so Mathcad handles it the same way as it handles other functions for which this is true, such as sin, ln, etc, and returns an element by element result. I was always taught that vectors are represented as a column, and therefore I would expect X*X^T to return a one element matrix. Unlike either you or Alan, I do not consider a one element matrix to be the same as a scalar.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Afte some short research I agree that I, too, am not aware of a definition for exponentiation of a vector and therefore a math prog seems to be free to implement it at its will. For me it would have been more consequential to interprete the square of a vector as the dot product of that vector with itself rather than to resort to auto vectorization. But then that may be a matter of personal taste.
According the 1x1 matrix - of course its not scalar and Mathcad is doing wrong in that respect, but often its simply convenient to look at a 1x1 matrix as a scalar.





