- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Make "too large to display" a function so I can use it in plot?? mathcad attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Make "too large to display" a function so I can use it in plot?? mathcad attached
I need help!
I have I long equation, and I am trying to solve for one of the variables in the equation:
K=f(a,W,K) --> solve for K, to make K=f(a,W).
I have attached the mathcad.
The solution for my solve function is too big, but I need to use this solution to create a plot. How do I do this??
Thank you!!!
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
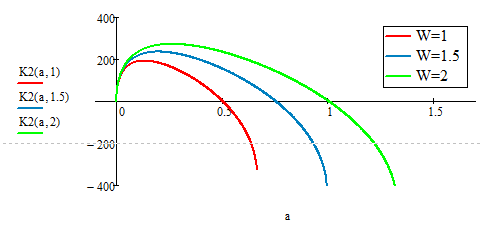
If the goal is plotting and tables of values, there are resonable numerical solutions using "root" or "Find"available. The reason for those "artefacts" we see when using root for a values greater than 2*W/3 are due to the fact that root delivers real roots for selected single values where it should return a complex number, I guess. So I think the graph produced with the sollve block is the correct one and function K1 should be rewritten to return NaN if a is greater than 2*W/3.
Another question. How can I add the errorhandling to K2 as I did it with K1. Do I have to define another function which is then asigned to K2?
- Using the "root" function
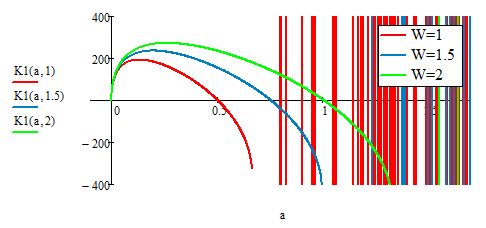
- Using a solve block with "Find"
Edited: Changed attached file, include modified solution with root (as decribed above) now
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
without units and using a substitution Mathcad is able to show the result, but I guess I won't make you happy. Due to the nature of the solution it cannot assigned a function. Details see attached.
Are you sure that solve should find a compact, unique solution?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I try to substitute it, but it can not work, even I try to substitute the simple one, it can not work too.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Look if the attached (based on the idea in a post of 朱 欣研 which seemed to have been deleted) makes sense.
Caution - takes quite a while to evaluate
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
hehe, because I think the method of exhaustion maybe no efficency on this problem, so I have deleted the reply...
I'm use another method, simplify it by hand, and use W=1, plot K(a,W)--a/W, seemly it only one point on it...Maybe wrong.

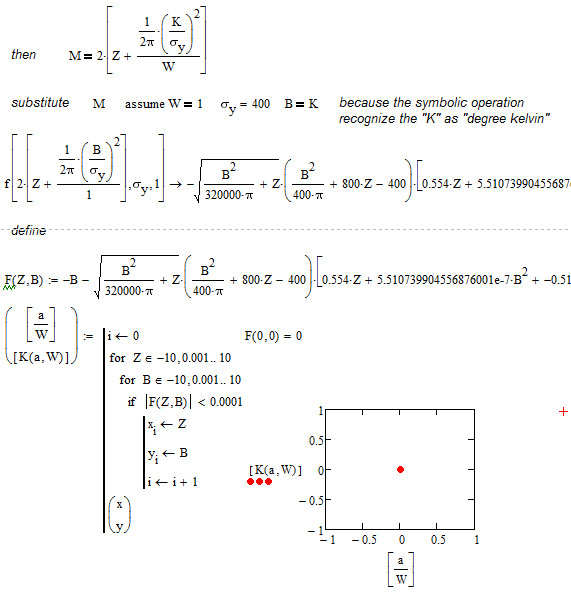
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not that much of value without the sheet (as mine, as I forgot to include it).
Look at the range for a and K in my solution and throw that in yours. Maybe you will see more than one point then.
After all - if you are going for a sulution using the "brute force" way with those nested for loops, it would not be necessary to make that long winded manual simplification and substitution process anyway.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah... I only want this function to be easily look and operate, and that big expression really annoying me to think about it. My simplify method go false on this mission.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
朱 欣研 wrote:
Ah... I only want this function to be easily look and operate, and that big expression really annoying me to think about it. My simplify method go false on this mission.
Unfortunately the necessary resubstitution will undo most of the simplification.
BTW you would not need B if you assign the expression directly a function with formal parameter K.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Jan Kowalski wrote:
Better look
But much less precision. For a better look AND correct values you would need
- a decreased tolerance value (and not one increased to 0.1)
- a decreased step value at least for K
- an increased number of cups of coffee to bridge the waiting time
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If the goal is plotting and tables of values, there are resonable numerical solutions using "root" or "Find"available. The reason for those "artefacts" we see when using root for a values greater than 2*W/3 are due to the fact that root delivers real roots for selected single values where it should return a complex number, I guess. So I think the graph produced with the sollve block is the correct one and function K1 should be rewritten to return NaN if a is greater than 2*W/3.
Another question. How can I add the errorhandling to K2 as I did it with K1. Do I have to define another function which is then asigned to K2?
- Using the "root" function

- Using a solve block with "Find"

Edited: Changed attached file, include modified solution with root (as decribed above) now
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The herizontal ordinate of the plot is a/w, thus K(a,1.5), is a/1.5, and k(a,2), is a/2, OK?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you plot with a/W on the ordinate and K(a,W) on the abscissa you will get a lot of graphs which cover/overlap/are identical with the red one (for W=1). So nothing new. This of course only applys if its possible at all to make the function dependable of the ratio a/W alone, which does NOT seem to be the case here as the graphs show. So either K is not supposed to be dependent of the ratio a/W or the original poster should check the formulas in my file against the one in his sheets.
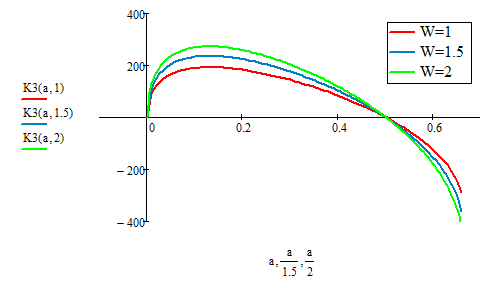
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Wow you guys are great. I never expected this much help!!
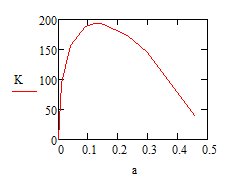
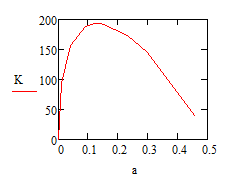
K is only a functon of sigma, a, and W. I am given the instruction to plot K vs. a/w. The plot I am creating is supposed to prove that the K function does not rely on the first bit:
W-2(a+rp)/W
This is why, I believe, we are getting the different scales for a/W.
I believe this is exactly what I need! Thank you!!!
Also - I should have noted this before - the domain is only between a/w = 0-0.5