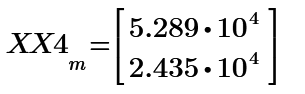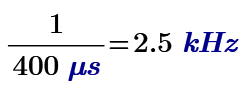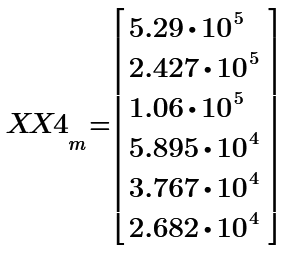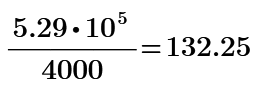MathCAD Spreadsheets - Need Help

[DJV]

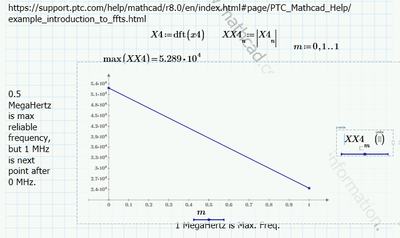
I have attached three files.  FFT1, FFT4, and FFT5.  I'm trying to learn how to do a fast fourier transform.  I begin with a 1 microsecond sampling rate, which provide a max. nyquist frequency of 500 kHz.  I multiply the number of points in FFT4 by a factor of 10, so the sampling rate becomes 0.1 microsecond, which provides a max Nyquist frequency of 5 MegaHz.  Then I again multiply the sampling frequency by 10 and produce a sampling rate of 0.01 microseconds and a Nyquist frequency of 50.  Can anyone take a look and confirm this theory?  

How do I reproduce a segment of the output FFT?  I want to reproduce the segment above n=50 MHz in the final spreadsheet.  

How do I reproduce the segment beginning with n=0 and ending with n=50 in the FFT5 spreadsheet.

I want to reproduce the original waveform as well..

Any assistance understanding this software would be welcome.

I also need to know what dft is doing relative to FFT.  I know it uses fewer points, are there any  deficiencies?

I need to know that what I'm doing is correct.

[ttokoro]

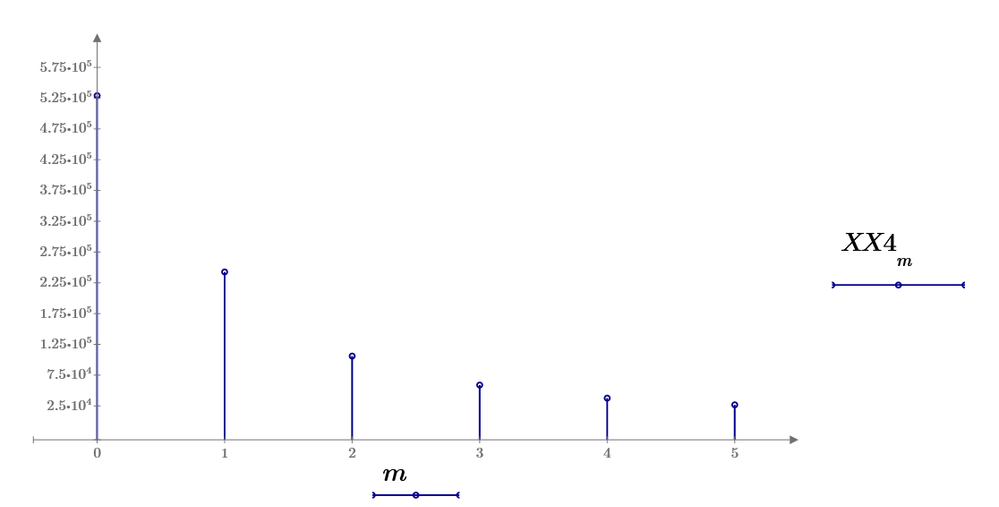
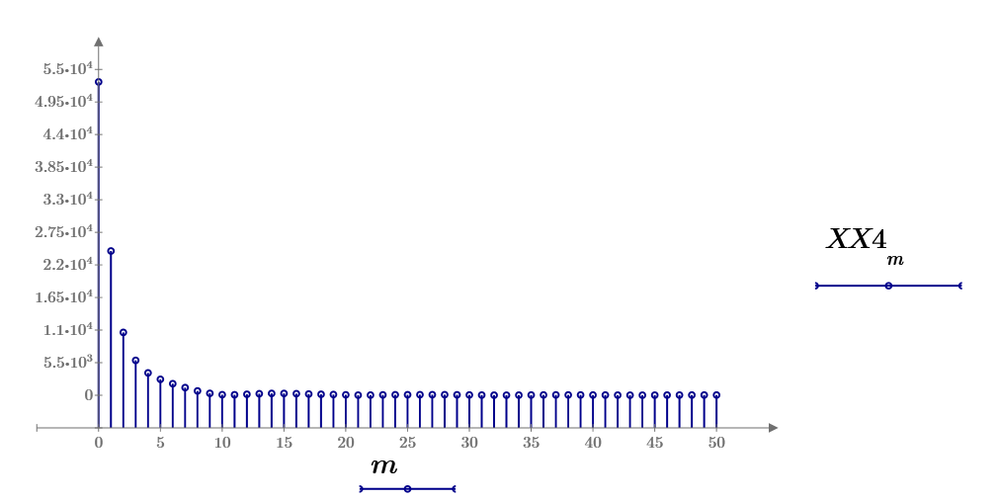
Your m is rows number. row 0 is DC spectrum. row 1 is fundamental spectrum of

[DJV]

Thanks for the tip.

Sincerely,

Del Ventruella

[ttokoro]

FFT4

Your m is rows number. row 0 is DC spectrum. row 1 is fundamental spectrum of

 row 5 is 5th spectrum.

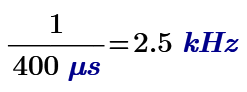
These  dft data show almost same value as FFT1's one because the data should divide the number of points of fundamental wave data. 

For DC spectrum 

[ttokoro]

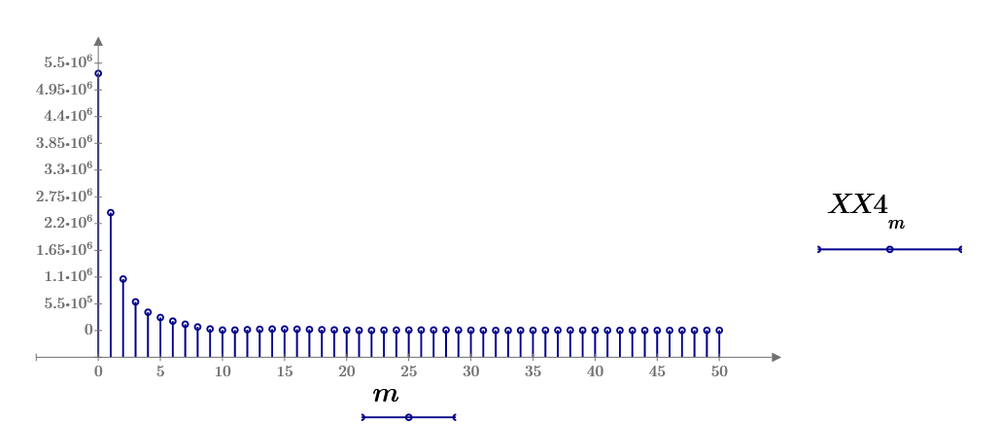
FFT5

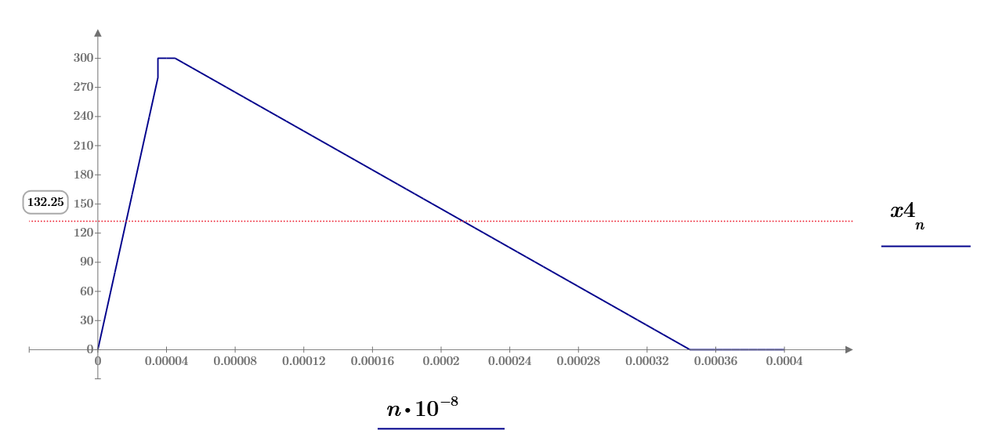
FFT5 shows spectra from DC to 50th harmonic. But the data shows same DC value for FFT4 and FFT1.

You can plot from 0 to 50th harmonic not only FFT5 but also for FFT4 and FFT1.

FFT1 can plot the spectra from DC to 200th. FFT4 can the one for 2000th and FFT5 can 20000th. But all data from DC to 200 are almost same because you using almost same waveforms.

FFT1 and 

This plot is as same as FFT5's one, it only devide y axis data by 100.

[DJV]

How do I get these plots to output the lollipops?

[DJV]

Alright, got it done.

[Fred_Kohlhepp]

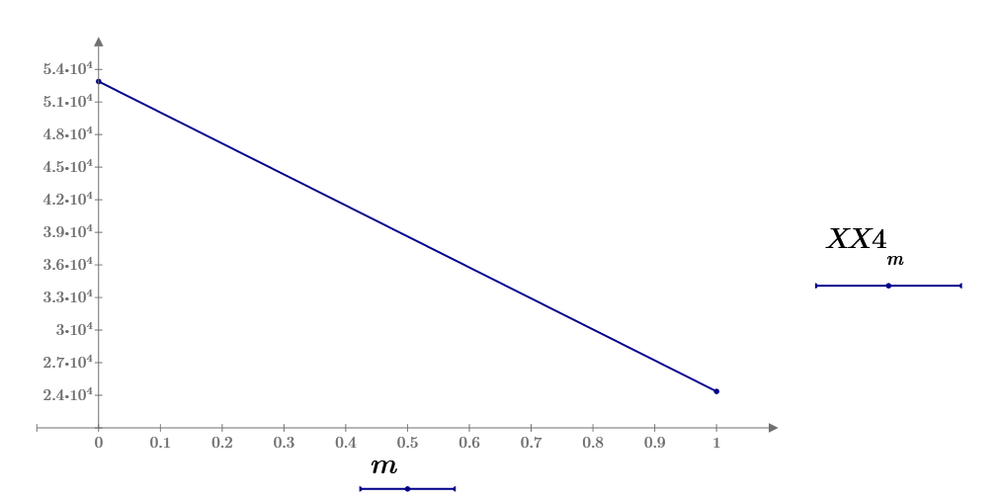
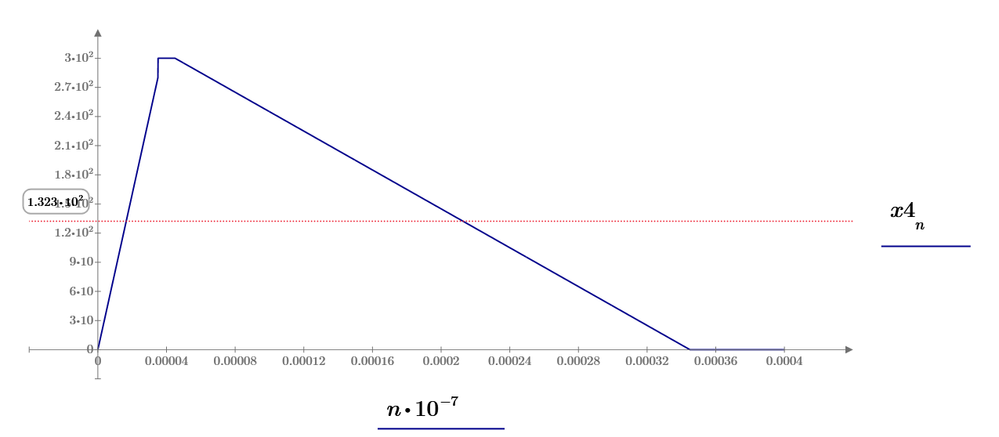
You aren't plotting against frequency, there are only two points in this plot:

You need to compute the frequencies for the ordinate axis.  Sample attached.

The "lollipops" are a stem plot,  (Look at plots/Change type.)