MathCad calculation error with infinite integration limit

[ChrisWilkinson]

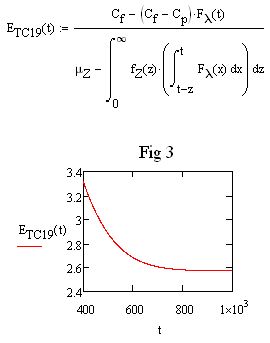
I have a problem with MathCad (v14) when integrating a function between zero and infinity as in the attached.

• The integration returns zero if the upper limit is set as infinity (from the dy/dx toolbar)
  
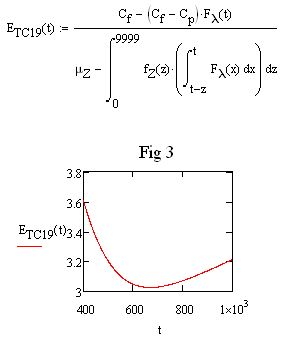
• Using a sufficiently large real number as the upper limit produces the expected result
  
• Adjusting TOL seems to make no difference
  

Has anyone experienced anything like this or found a solution?

[MikeArmstrong]

This is what I get using M15.

And

Mike

[MikeArmstrong]

I also get the same as infinity if I make the upper limit t.

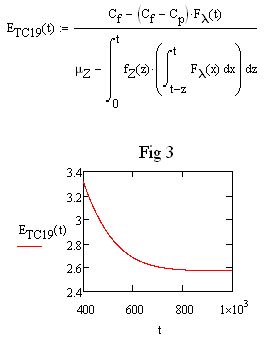
Mike

[ChrisWilkinson]

Interesting and also interesting that you get the same result with M15 as I got with M14.

I also found I could get the same result as infinity with some small fixed value for the upper limit.

This seems to be plainly a bug but I'm not sure if or how I should report it or if there's any point.

[wayne]

Chris Wilkinson wrote:

Interesting and also interesting that you get the same result with M15 as I got with M14.

I also found I could get the same result as infinity with some small fixed value for the upper limit.

This seems to be plainly a bug but I'm not sure if or how I should report it or if there's any point.

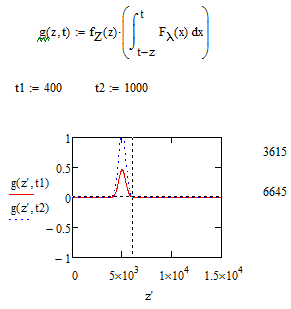
There is not a bug,

You need to study the function inside the integral, it is very nearly 0 except for a spike as shown in the picture above. I suspect there is a negative spike, canceling the one shown below, somewhere between the highest numerical upper limit you tired and infinity.

[MikeArmstrong]

Nicely spotted Wayne.

Mike

[RichardJ]

It's not a bug, it's just a limitation of numerical integrators. As Wayne points out, the kernel of the integral is a peaked function. The numerical integrator works in steps, and if you make the range of the integral too large relative to the width of the peak it can just step over it. It doesn't have to be infinity, it just has to be too large.