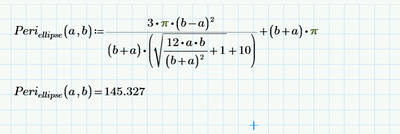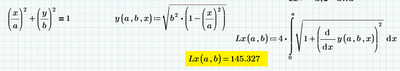Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Mathcad Community Challenge March 2024 - Perimeter of an Ellipse
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad Community Challenge March 2024 - Perimeter of an Ellipse
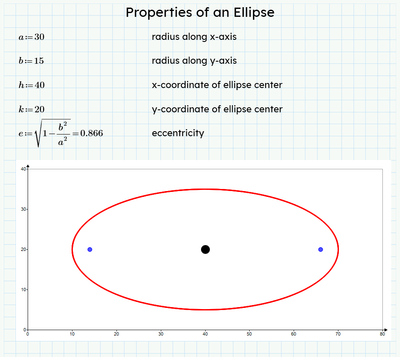
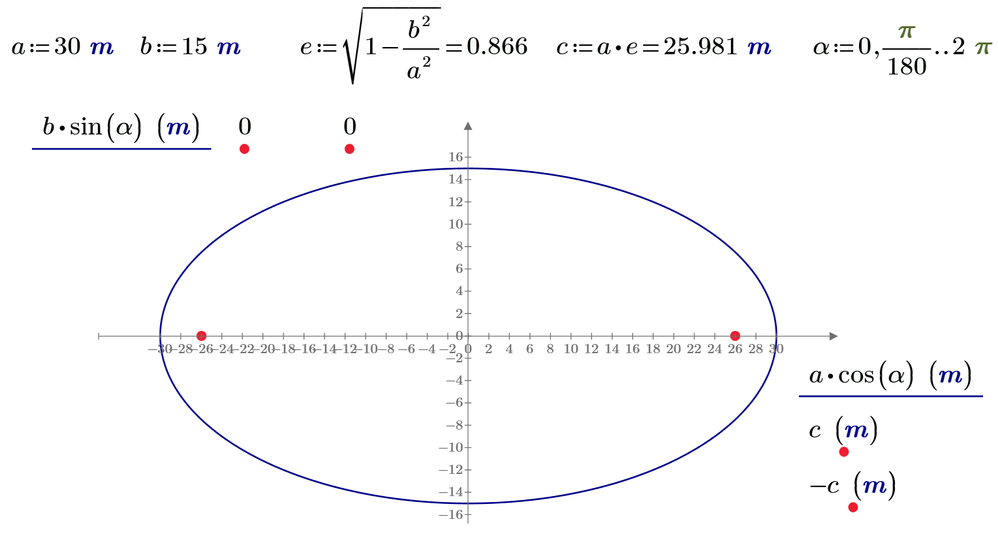
I am shocked that I have walked the surface of this planet for over 5 decades without realizing that there is no exact closed-form solution for the perimeter of an ellipse. In school, we learn the perimeter of shapes like triangles, squares, rectangles, circles, parallelograms, and so on, but I feel like schools and teachers conveniently skipped over ellipses.
(An ellipse, in case it’s been a while, is the set of points where the sum of the distances from two points – the foci – is a constant.)
Your challenge, should you choose to accept it, is to correct that oversight. Create a Mathcad worksheet that:
- Derives, depicts, or shows one (or more) of the various approximation formulas / methods for the perimeter of an ellipse.
- Create a calculator whereby someone can change the values of the semi-major and semi-minor axis lengths in order to find the perimeter.
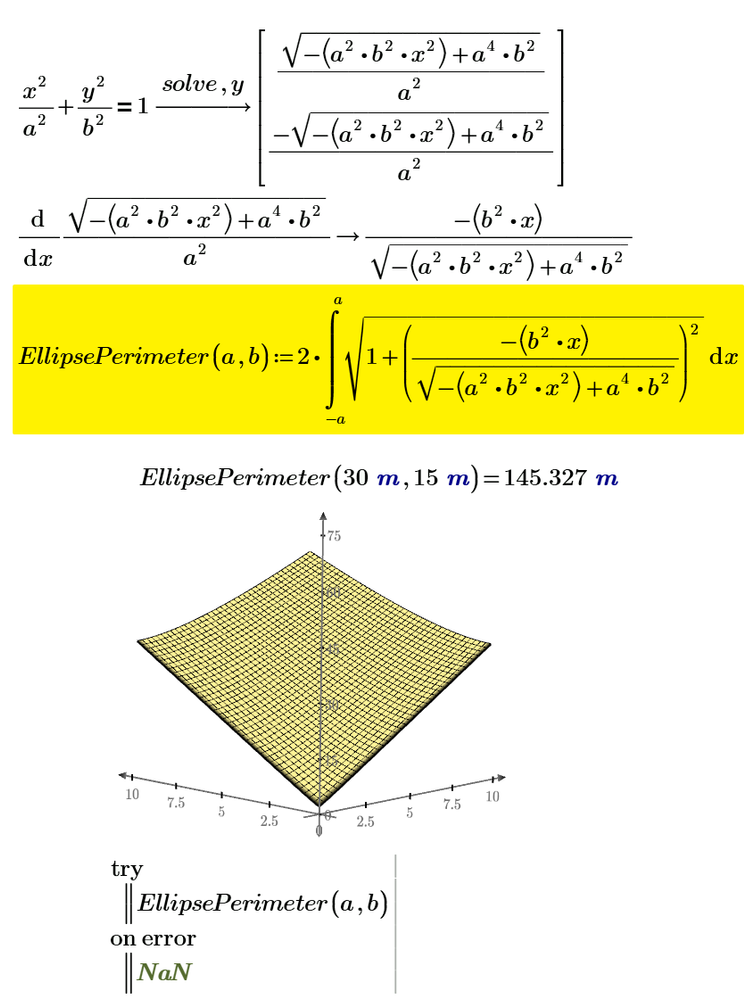
- Create a 3D plot of the perimeter as a function of the ellipse semi-major and semi-minor axis lengths.
Although there is no exact solution for the perimeter of an ellipse, this is a fairly well-documented problem. Therefore, your documentation in your worksheet is key! This worksheet should be able to stand on its own and be understood by someone with a basic knowledge of calculus (since integrals and infinite series are involved).
Good luck and have fun!
Find the Mathcad Community Challenge Guidelines here!
- Labels:
-
Mathcad Challenge
-
Puzzles Games
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
File enclosed Prime Express 9.0
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
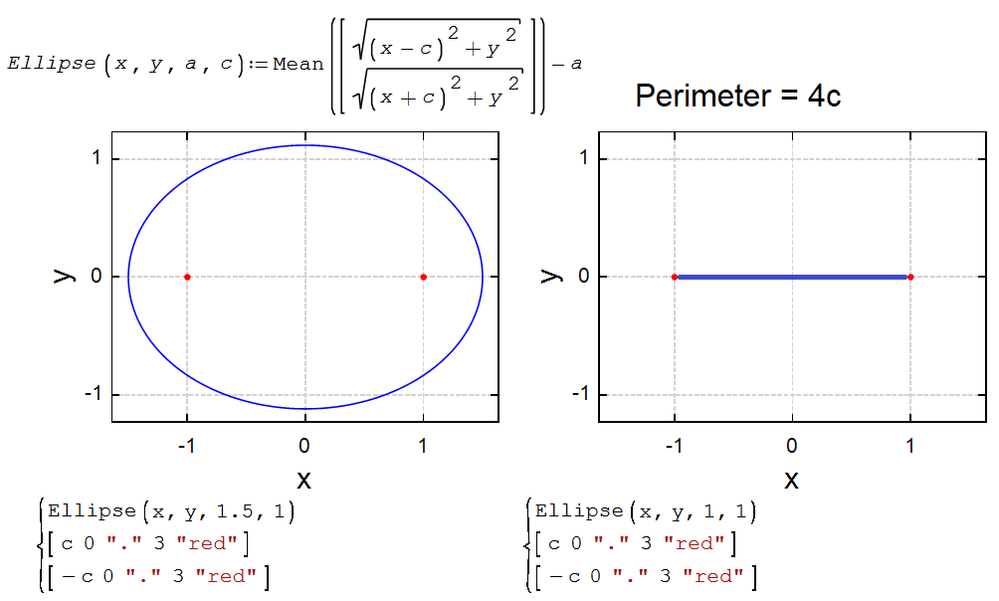
I once won such an argument a long time ago - I showed two ellipses (Mean) for which there is an exact formula for the perimeter. One of them is a circle, and the second - see the picture.
A more challenging and interesting problem is the Cassini Oval (gmean) and the Cayley Oval (hmean)!
PS
“The race course was a large three-mile ring of the form of an ellipse..”
Leo Tolstoy. "Anna Karenina"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
More interest plot
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My attempt attached (excludes part 3 as 3D -plotting not available in Express).
(As I couldn't do the 3D plot in Prime Express, I decided to do it in M15 - see below.
The plot is really boring!).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
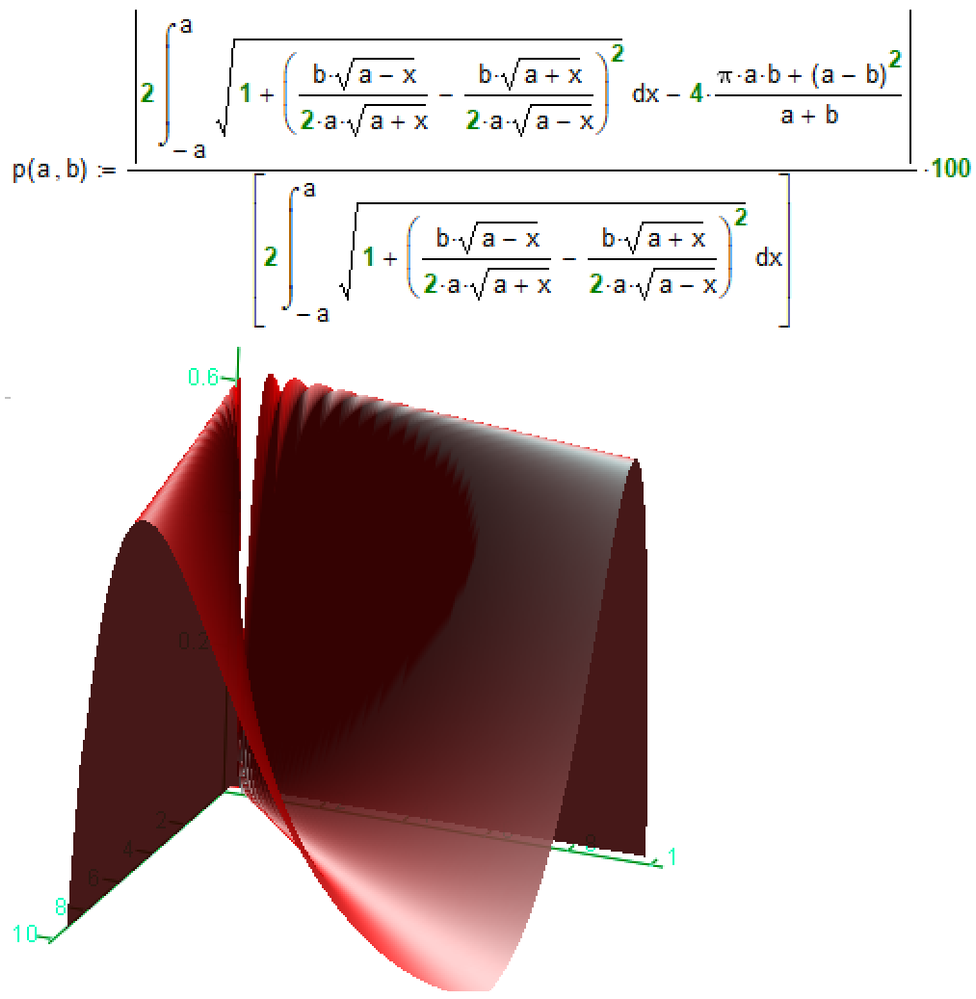
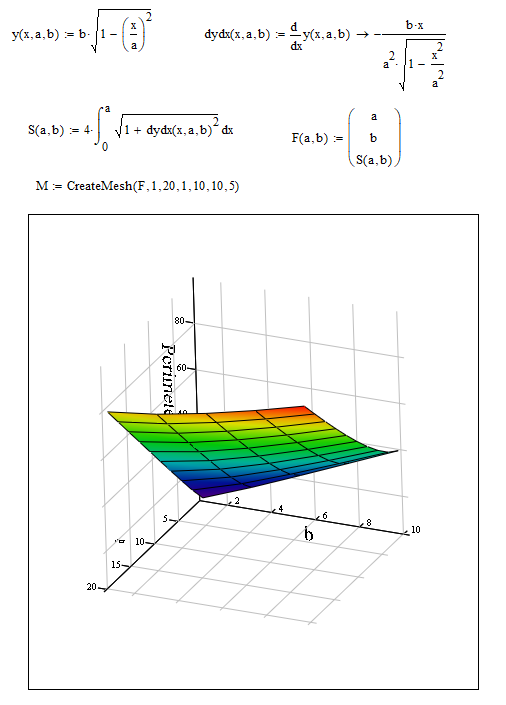
Every problem deserves a numeric solution. I'll leave the complicated derivations for the experts. This was good enough for Archimedes so good enough for me too. Bit too much to make the 3D plot at this time.
Prime 7 attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Am enjoying the posts so far so want to add a quick from 1st principles approach:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Just could not resist it. A page of matrices and voila 3D plot in express.
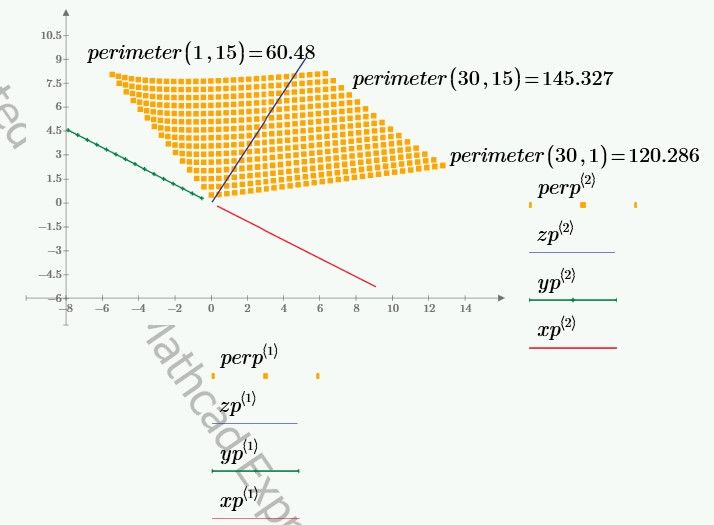
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
DJF,
In the blog write-up, how should I refer to you in the blog write-up?
Thanks, Dave
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
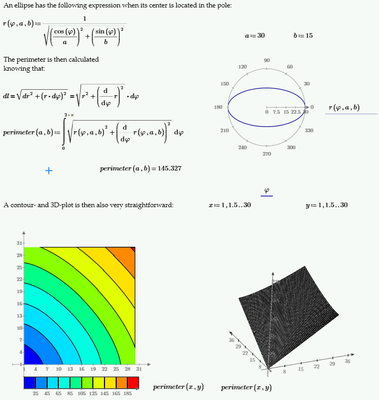
This is one I couldn't let go. This question is easily solved using polar coordinates:
Calculation speed can be increased using the ellipse's symmetry by limiting the integral between 0 and pi/2 and multiply that value by 4. With a similar technique surface, moment's of inertia and so on are easily calculated.
All this is pretty basic, really. The fun starts when adding parameters to the equation, for instance making Superellipses and even (far) beyond. In the following article I made use of Mathcad Prime to illustrate the above: https://www.athena-publishing.com/series/atmps/issbg-22/articles/260/view
Enjoy!
Bert Beirinckx
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@AlanStevens wrote:
Alan
"... which is exactly ..."
exactly?? The perimeter of a circle can't be calculated exactly, either. 😞
The closed form for the circle circumference is actually a deception, because the infinite series is hidden in the constant pi, which we have invented for the ratio perimeter: (2*r) for the ellipse with a=b=r.
So there is no real difference between the perimeter of a general ellipse and a circle other than the pi approximation key being available on every pocket calculator...
I, too, enjoyed Bert's article.
BTW, I nice video on the topic of the ellipse perimeter can be seen here on Stand-Up Maths channel: Why is there no equation for the perimeter of an ellipse
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I would say the circumference of a circle is exactly 2pi.r. Of course, that doesn't mean we can get an exact numerical value. However, let's not worry too much about semantic interpretations! Perhaps it would have been better if I'd replaced the words "is exactly" by " has the closed form solution".
I also liked the Stand-Up Maths video.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@AlanStevens wrote:
I would say the circumference of a circle is exactly 2pi.r. Of course, that doesn't mean we can get an exact numerical value. However, let's not worry too much about semantic interpretations! Perhaps it would have been better if I'd replaced the words "is exactly" by " has the closed form solution".
I also liked the Stand-Up Maths video.
Alan
What I meant was that 2* pi *r just looks like a closed form solution but it actually isn't. It just looks that way because we decided to choose a simple looking greek letter as an abbreviation for he involved infinite sum. That way I guess we could also derive "closed form" solutions for the perimeter of an ellipse with any other ratio a:b as well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Val Ochkov has asked me to post this picture:
Val says he has just been banned from the forum! I hope that's just a temporary glitch as he's been a great supporter of Mathcad and the forum for years.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess and hope that it is not a ban on the part of the forum operators, but on the part of the Russian rulers.
If this is true, the use of a VPN could probably help Val to overcome this hurdle.
If not, maybe the admins can say something about it -> @admin , @AndrewK , @Jaime_Lee
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Seems to have been a forum ban (Val sent me the following image):
@Werner_E wrote:
I guess and hope that it is not a ban on the part of the forum operators, but on the part of the Russian rulers.
If this is true, the use of a VPN could probably help Val to overcome this hurdle.
If not, maybe the admins can say something about it -> @admin , @AndrewK , @Jaime_Lee
I assume this was an automated system response. Perhaps an actual PTC person could overturn it?
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the additional information @AlanStevens we are looking into this now.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A friendly hello to the puzzle group,
I only have MC14 available. Therefore I couldn't read all the posts. Therefore, here is just a reference to a very good approximation function for the circumference of the ellipse - it is Ramanujan's formula. I don't know of a better one from the literature. I have attached them, but I cannot provide the desired 3D plot. I'm asking for help here.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
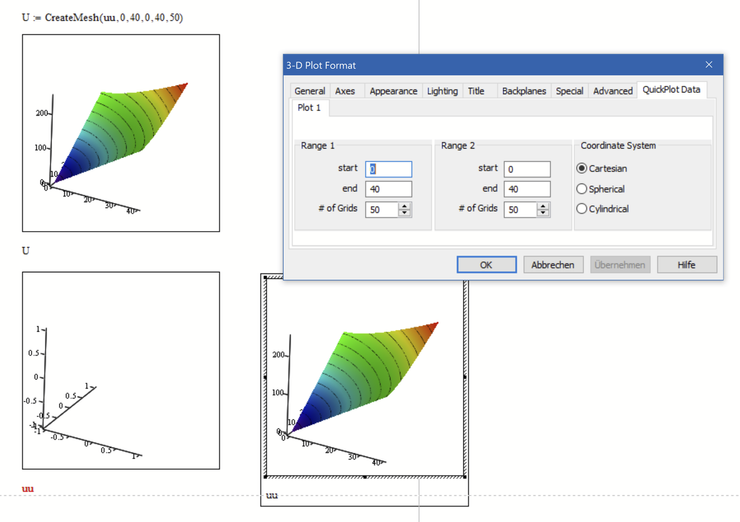
Hi,
Your function uu() has two parameters so producing a 3D plot is simple with the matrix() function.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I use MC14 and therefore cannot load your file. Would you please reply in the appropriate file format? I haven't created a 3D plot yet. They were mostly vicious equations that I solved using equivalent minimum problems.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
Mathcad 12 version you should be able to open in Mathcad 14
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you. It helped 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@terryhendicott wrote:
Hi,
Your function uu() has two parameters so producing a 3D plot is simple with the matrix() function.
Cheers
Terry
I would strongly vote against using the matrix function to do the job! It may give a decent result here but you can't use it to provide intermediate values (non-integer arguments) or negative arguments.
The way to go sure is using the CreateMesh() function which is exactly made for this.
We could also plot the function uu directly but in this case it will fail because the function uu is written in a way so that it yields non-real values for negative input arguments. And because the standard interval for a 3D Quickplot is from -5 to 5, this makes the whole plot fail.
But if we force the argument values to be in the desired range, plotting uu directly works as well.
Nonetheless I sure would vote for using CreateMesh when creating 3D plots of functions in 2 variables.
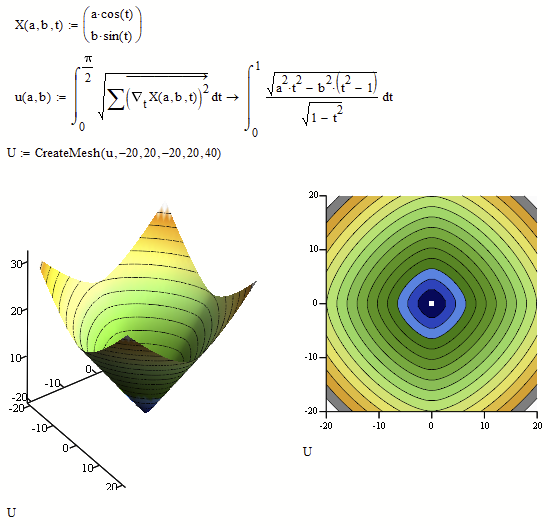
BTW, here is a different approach allowing for negative input values, too (even they may not make much sense in the context of the ellipses here)
Can someone derive an equation for the contour lines ??
You should be able to open the xmcd file posted by Terry initially with your MC14!?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, now it runs. Do not know why it was in opposite before. At my age, nothing surprises me anymore 😉 .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Using Ramanujan Approximation.
From MARK B. VILLARINO
Nice plots already done - see ValeryOchkov AlanStevens
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Reminder to everyone that we're now in the last one-third of March! Great participation thus far.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
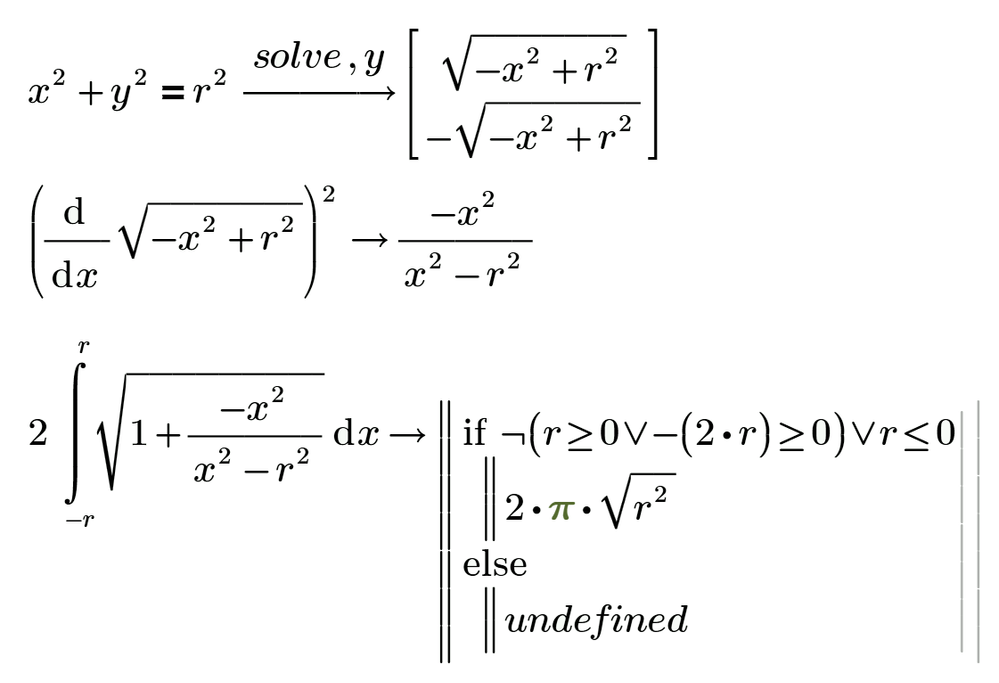
This isn't really a response to the challenge. The attached sheet poses a slightly different question.
I started out to answer the challenge; seemed easy to simply integrate along the curve and easier to do it in polar coordinates:
For the ellipse posed in the challenge:
Then I looked at the other responses. . . .
And went back and checked, did the same thing in cartesian coordinates:
So why won't polar work?