Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Maximum of graph
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maximum of graph
In the attached prime worksheet I am graphing the shear and moment in a beam. Is there a simple (maybe 1 or 2 lines) for determining the minimum or maximum values on either graph? The three lines I have for determining the maximum is convoluted and inaccurate (the maximum is 8kip*ft, not 5.9 kip*ft).
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for providing the picture.
Its a Prime specific problem and has to do with the different handling of units introduced in Prime. Unfortunately a lot of routines, especially numeric iteration algorithms like maximize, have not been adopted and tend to fail when used with units This was a problem in some cases in MC15, too, but not to that extent. Things got worse, even if the new unit handling is an improvement in general.
While numeric integration and numeric algorithms like the one used in maximize have its precision limits and can not be expected to get the 100% correct result 8 kip ft, the result given (approx. 6 kip ft) is not acceptable at all.
There are workarounds I could think of and depending on the situation they all have their benefits.
Best choice in your case seems to be to change the system variable TOL before the definition of the numeric integration.
You can do this globally in the calc ribbon or in the sheet (which makes for better doc) and it doesn't help to set it too low - results won't get better:
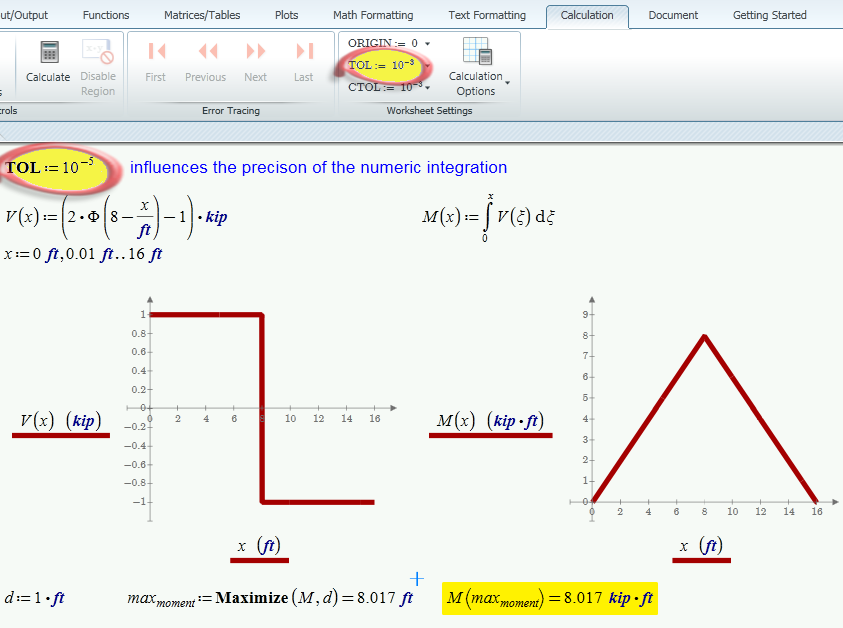
BTW, even though Mathcad seems not to care, you should not use a variable of integration as a limit in the same integral. Thtas the reason I changed you x to xi.
One other way to copy with the problem is to completety do without units, but this would mean to pass on one of the outstandig features of Mathcad.
A compromise is to get rid of the units temporarily by defining a unitless dummy function to maximize. You can of course additionally play around with TOL.

WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I can't read your worksheet because it's in Prime 3.1 format, but look up the maximize and minimize functions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I can't read Prime 3.1 format either.
Do you graph a function or do you graph one vector against the other?
in the latter case you may look up the functions localmax and localmin.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have functions to plot the data: here's the end result (it's a PITA to get Prime sheet data intio this forum). There's programming involved in getting Vd(x), so I can't evaluate due to Prime Express.

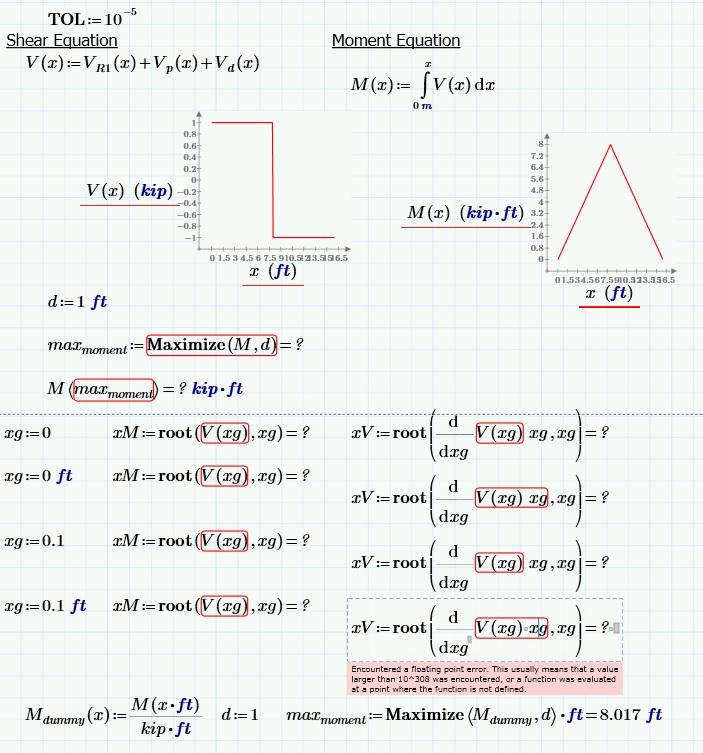
It should be possible to find the x-value of the extreme(s) for M(x) by finding the root(s) of V(x), because that's the derivative of M(x):
With a guess value xg:=0, find an extreme of M(x) with xM:=root(V(xg),xg), then the maximum of M(x) is found as M(xM).
If the root is not found, change the guess value.
For V(x) you can simply read the extremes from the graph.
To do it numerically you procede likewise as with M(x), but you need to find the roots of the derivative of V(x).
xg:=0 xV:=root(dd(V(xg),xg),xg). {Where dd(F(x),x) is the derivative operator to take the derivative of f(x) wrt x.}
Changing the guess value xg will allow to find other extremes.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for providing the picture.
Its a Prime specific problem and has to do with the different handling of units introduced in Prime. Unfortunately a lot of routines, especially numeric iteration algorithms like maximize, have not been adopted and tend to fail when used with units This was a problem in some cases in MC15, too, but not to that extent. Things got worse, even if the new unit handling is an improvement in general.
While numeric integration and numeric algorithms like the one used in maximize have its precision limits and can not be expected to get the 100% correct result 8 kip ft, the result given (approx. 6 kip ft) is not acceptable at all.
There are workarounds I could think of and depending on the situation they all have their benefits.
Best choice in your case seems to be to change the system variable TOL before the definition of the numeric integration.
You can do this globally in the calc ribbon or in the sheet (which makes for better doc) and it doesn't help to set it too low - results won't get better:

BTW, even though Mathcad seems not to care, you should not use a variable of integration as a limit in the same integral. Thtas the reason I changed you x to xi.
One other way to copy with the problem is to completety do without units, but this would mean to pass on one of the outstandig features of Mathcad.
A compromise is to get rid of the units temporarily by defining a unitless dummy function to maximize. You can of course additionally play around with TOL.

WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you all very much, I can always count on exceptional help here!
Richard Jackson: Thank you, because folks can't open Prime 3.1 (had I known I would've stayed with Prime 3.0) I will post screen shots in the future.
LucMeekes: Thank you, I have attempted using the root function with various guess values (with and without units) but was not successful. Similarly I did not find luck using the root function of the derivative of Shear (V). Using the root function of derivative I received this error: “Encountered a floating point error. This usually means that a value larger than 10^308 was encountered, or a function was evaluated at a point where the function is not defined.”
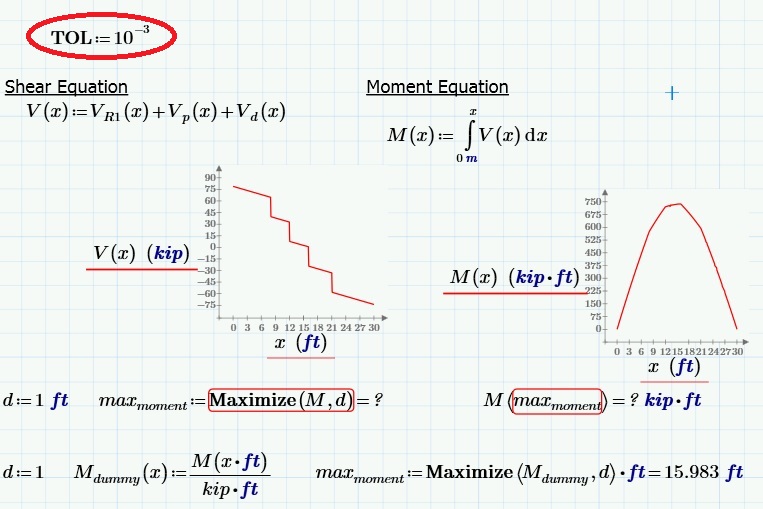
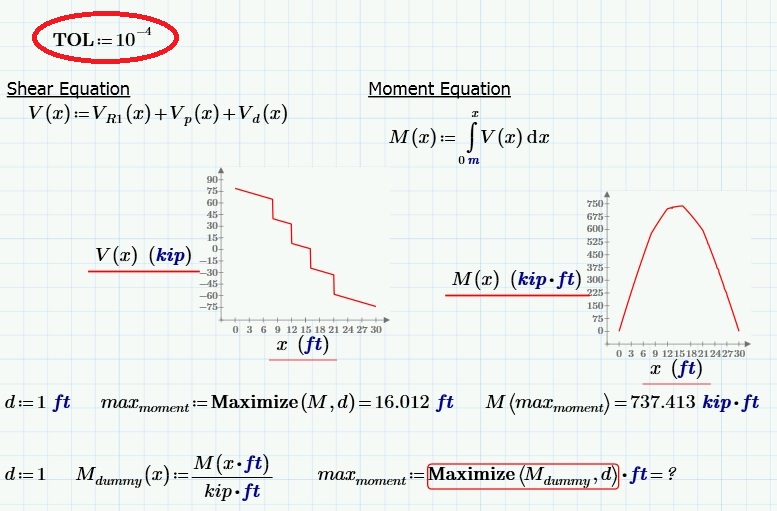
Werner: Thank you, I’m not sure how changing the TOL value makes the maximize function successful; values from 10^-5~-15 were not successful in my sheet. If a worksheet contains many integrations maybe the TOL will have to be adjusted for each. Creating the unitless dummy function seems to make the maximize function work. The graphs of shear and moment will get much more complicated with many local mins and maxs, I’m hoping this is the answer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Interesting setting the convergence tolerance to 10^-3 causes the dummy moment equation to work and the original moment question to not find a solution. Setting the convergence tolerance to 10^-4 cause the opposite to happen.