Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Minimize function strange result
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Minimize function strange result
Hi all,
I hope this is the right sub-forum to post this address.
I am trying to make use of some Mathcad in-built capabilities, like for instance the Minimize or Maximize function.
Please have a look at the attached file. I have some functions defined there which ultimately are used inside the final function called Function1 (blue background).
For Function1, I want to apply the mathcad defined Minimize function, which needs the variation intervals for the variables of the function to be defined (along with guess values). I can do that OK, and I do get a relevant result when applying the Minimize function on Function1 (the result consists of the variables values, within the defined interval for each variable, for which Function1 will be minimum). I store this result in the variable called "Result" and then I compute the value of the Function1 function with the elements of the "Result", aiming to obtain the minimum of Function1 (yellow background).
The problem that I have is that it does not seem to be a minimum; meaning I can find other values for the variables, within the defined intervals, for which the value of Function1 is even smaller (see area marked in green). So am I doing something wrong or is this simply a strange function?
Regards,
Cristian
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, the reason why you (Cristian and Rich) get the same result on the first run is due to the random number generation, which is pseudo random: Whenever Mathcad starts up with the same sheet, doing the same calculation(s), the sequence of random numbers is the same.
The reason you don't get (almost) exactly the 'absolute' minimum is because if you want that, you have to set the parameters correctly (that is to the edge), which is what I did in successive runs to verify Werner's observation. With every run I limited the range of each variable between a found minimum and the correct edge.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad will find a relative minimum, no necessarily the absolute minimum.
Maybe your problem is conditioned in a way that you have a lot of local minima very near and changing the guess values slighty may yield one or the other.
Its strange that I get a better result when I increase the value of CTOL - would have expected the opposite effect.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Mathcad will find a relative minimum, no necessarily the absolute minimum.
Maybe your problem is conditioned in a way that you have a lot of local minima very near and changing the guess values slighty may yield one or the other.
Its strange that I get a better result when I increase the value of CTOL - would have expected the opposite effect.
Werner, did you do anything else apart from assigning CTOL a value of 10^-1? Because if I do that, the result in my file does not really change! Please see the attached file called minmax_no_external_file_with_CTOL_set_to_0.1.xmcd
On the other hand, I was able to find a smaller value by doing these things simultaneously:
- decrease the value of CTOL (down to 10^-7)
- set the guess values at the beginning (or end) of their variation interval
By doing this, I did find a minimum slightly smaller than the one I could manually find, see attached file called minmax_no_external_file_with_guess_values_set_at_the_beginnig_of_the_variation_interval.xmcd
Now I would be close of trusting this minimum I found, but I am really puzzled by the 2754.3 value you present above and which I cannot replicate. Would you kindly screenshot the results of the minimize function (the value of the variables) that you get when setting the CTOL to 10^1 on your machine? Thanks.
Regards,
Cristian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> Werner, did you do anything else apart from assigning CTOL a value of 10^-1?
No, nothing. I just tried again with the same result. And I also get the same low result with CTOL set to 1 or even to incredible 10! Not sure, why this works.
But you have to set CTOL before the solve block (I used a global assignment for the screen shot) or via menu (Tools - Worksheet options - Built-in Variables).
EDIT: I just opened your file and get the same (low) result. See the screenshot:
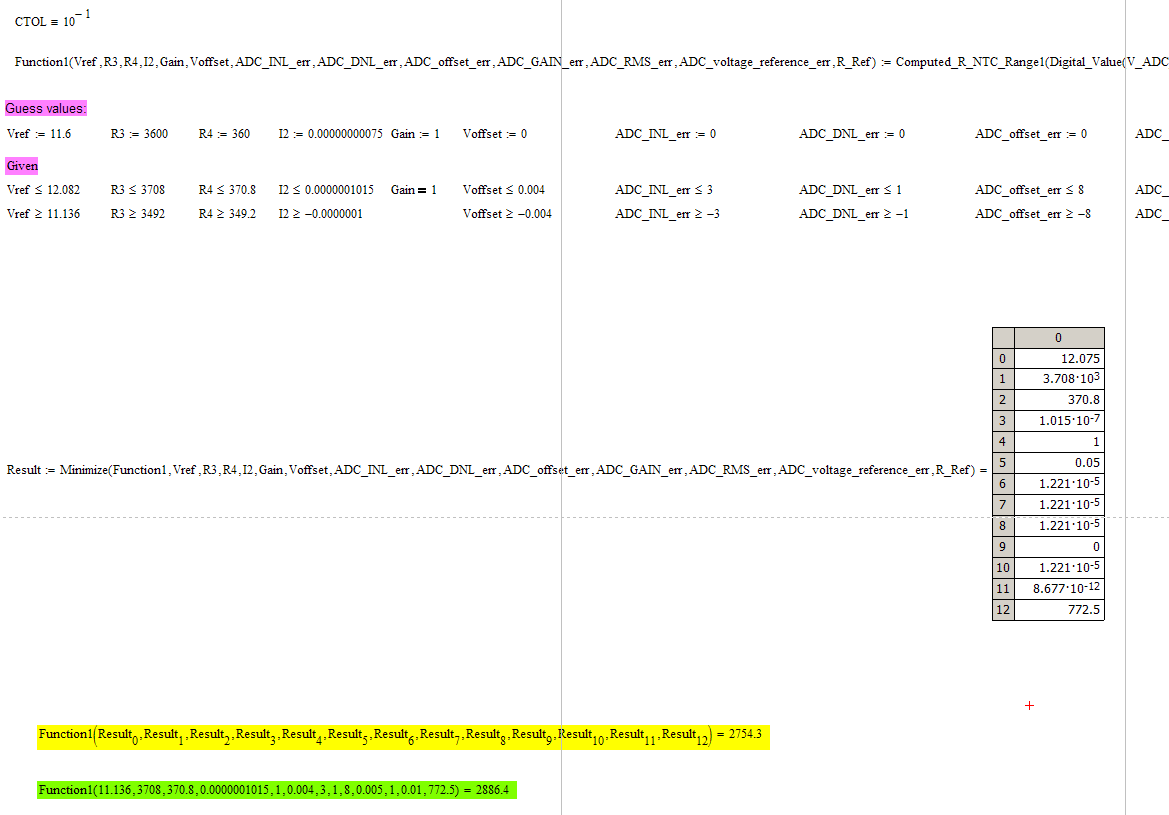
I am using Mathcad 15 M030.
Here are the 12 values for easier copy and paste:
12.075438396003252
3.708e3
370.8
1.0150000000000001e-7
1.0000000000000222
0.05
1.2210011707882724e-5
1.2210011707882724e-5
1.2210011707882724e-5
0
1.2210011707882724e-5
8.676833784435876e-12
772.5
When I open the other file (with CTOL = 10^-7) I see the result 2886,2.
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
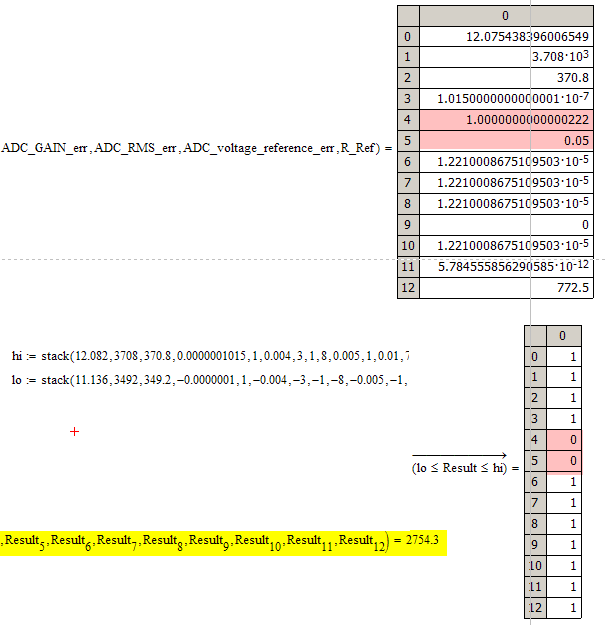
One additional remark: The constraints in that kind of solve block are soft constraint. So you may notice that nit all values in result are within the desired range (see the screenshots at the end.
Furthermore, as you don't allow any changes on "Gain", it has to be 1, why do you include it as an argument in "Function1". Omit it and call the other functions with 1, instead if Gain.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I just posted a reply to your earlier message expressing my surprise to the Voffset being outside the constrained boundaries, but I noticed that you touched on this point in your last message above, so I deleted it. It is great to see this, however I am puzzled about the notion of "soft constraints". It is like they are not really constraints...
Anyway, judging from your screenshot in your message right above this one, I see two situations, the second being significantly better in the sense that the second one seems to have much smaller variations of some variables outside the constrained boundaries.
What did you do differently in between the two?
Anyway, point taken regarding the Gain variable. I will "hard code" it as a 1, for the purpose of this calculation. In practice, it corresponds to an operational amplifier set in a repeater configuration, and in the future we might change its gain; but at the moment it is simply 1, thanks for suggesting this improvement.
Regards,
Cristian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So am I doing something wrong or is this simply a strange function?
Neither. It is the nature of non-linear solvers. They are iterative. They start at the guess values, then head downhill on the error surface until the error changes by less than a certain amount, and then stop. In Mathcad the built in variable CTOL determines what "less than a certain amount" means. So if your error surface has many local minima, or large areas that are nearly flat, the solver may not find the global minimum.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for your replies!
I was out of office for a couple of days, but I will give it a try (playing with the CTOL value).
I am really curious to see what the real minimum of this function is!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A numeric algorithm will always present you a local minimum and it depends on the guess values, the given allowed tolerances and of course the nature of your function.
So you will need a lot of luck to find the absolute minimium of your function, I guess.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
A numeric algorithm will always present you a local minimum and it depends on the guess values
See please Video Link : 1460
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your minimum value for Function1 is somewhere near 2975.
With thanks to the neat algorithm that Viktor Korobov made, and Valery Ochkov pointed to https://community.ptc.com/t5/PTC-Mathcad-Videos/Local-amp-Global-minimum-of-the-function-f-x-y/m-p/440019#comment-1814.
I've expanded it to functions of an arbitrary number of parameters

See attachment.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
By the way, if you wonder why the minimum I found (2975) is larger than what e.g. Werner (2886.4) found?
The reason may be because I changed the constants 750, 3600 and 360 in the formulae to the variables (R_ref, R3 and R4 respectively) I think they should be.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes wrote:
By the way, if you wonder why the minimum I found (2975) is larger than what e.g. Werner (2886.4) found?
The values which result in 2886.4 were not my findings - the were already in the sheet and I guess Cristian found them by some means.
What I did was simply to increase(!) the value of CTOL from the default 10^-3 to 10^-1 and Minimize found better values which yield a result of 2754.3. I still don't understand why increasing CTOL gets me better values.
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Possibly because it gives the variable I2 much more range than the limited +/- 10^-7 it should have according the OP.
I've rerun the brute foce/Monte Carlo algorithm over 20000 runs with R_ref, R3 and R4 back to 750, 3600 and 360 in the formula for Computed_R_NTC_range1 and now found 2898.6 as a minimum. But I still think my 2975 is the better result.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes wrote:
By the way, if you wonder why the minimum I found (2975) is larger than what e.g. Werner (2886.4) found?
The reason may be because I changed the constants 750, 3600 and 360 in the formulae to the variables (R_ref, R3 and R4 respectively) I think they should be.
Luc
Not really. These values must be fixed. The whole function models the calculation that would need to take place inside a microcontroller which must then determine a resistance value in a network that is feeding the ADC. When computing the digital value that could come out of the ADC, the extremes of the resistors variation interval must be used, of course. But when the microcontroller computes the resistor value, it only knows the conversion result and the nominal values of the external components.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK.
In which case the minimum would be (near) 2898.6.
Note that the Monte Carlo method that I used does not depend on any tolerance setting, but instead on the number of runs. You might consider increasing that a factor of 10 to see if the result is much different.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It does depend on the number of runs but also on ... luck, does it not? Of course you can minimize the risk by increasing the iterations, but it is never really going to be 0, is it?
Then again, even an iterative solver suffers the same : it will never really give you the absolute minimum, but the minimum with a tolerance.
Anyway, can you share the method you applied Monte Carlo on this function? I searched the help (I have Mathcad 14) but yielded no results when searching for Monte Carlo, or Monte-Carlo.
The minimum is significantly smaller than 2898.6.
As mentioned above (in a post probably not yet visible because it is awaiting moderation - I attached some files) I can find a minimum even smaller than 2886.4 - which is the value I managed to find manually (maybe by luck).
If I play with the CTOL value (decreasing it sharply) and if I set the guess values to the beginning or end of the variation interval (as opposed to the middle, as in the initial example) I get a minimum of 2886.2
Regards,
Cristian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I agree, Monte Carlo is luck, but minimize is tolerance. You should be able to get the input values for each of the parameters at the minimum, and check if they are within their respective range and check the result.
The Monte Carlo method (implemented in that Global_Extreme() function) is attached to the post where it is presented, here above: Re: Minimize function strange result.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Playing around with a Monte Carlo simulation for a while (refining by narrowing the allowed range of the arguments) I come to the conclusion, that you get your minimum if you choose argument values from the end of your ranges - mostly the upper bounds (in red below), but three times the lower bounds (green) as well (Gain remains 1):
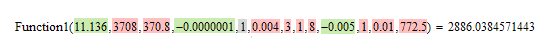
I suspect that you will not be able to beat 2886,038457 with arguments all within the allowed range.
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Checked.
You're right, Werner.
(OK, I beat it by 2e-11 ![]() , with a result of 2886.03845714428, but at the same input values.)
, with a result of 2886.03845714428, but at the same input values.)
Luc
Incidentally,
I improved the Monte Carlo algorithm. It was transposing the variables matrix a bit too often. Now it runs 1 million runs in about 20 s on my machine.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's a much faster way to get there. I've been meaning to implement simulated annealing for several years (some of you have probably got tired of me saying that!), and I finally did it. It finds the location of the global minimum in a few seconds, even in this pathologically nasty example. What surprises me a little is that minimize is not able to refine it to the true minimum, even when CTOL is set to 10^-15.
For more about the algorithm and it's implementation, see here: Minimizing a Function using Simulated Annealing
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc,
I must be doing something wrong... I just downloaded the file you attached at your message above (message at Apr 30, 2016 2:54 AM), opened it and then chose the "Calculate worksheet" option (Tools->Calculate->Calculate worksheet (Ctrl+F9)). The result is 2894.493, quite far away from the 2886,038457.
And what is concerning to me, the time needed to run is indicated (by time(Time0)-Time0 formula) as being only 2.121seconds, and I do not have a particularly powerful machine (it is a 2 years old I7 with 8GM RAM, but I have doubts this is the main reason).
Also another element I do not understand is the reason for which you introduced R_NTC_test and FS as variables in the main function, and how you did it (I am intimidated by the small black square at the exponent of R_NTC_test and FS variables definition; I am not sure how you obtain that and what it represents)
Admittedly, I am really a noob in Mathcad, although I have been using it for may year now, but not at such a level.
Regards,
Cristian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Did you change the number of runs up to 1 000 000?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is already set to that, in the file you attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I takes a bit more than 2 seconds for me too, and I get also 2894.493. It is rather suspicious that I get the exact same number as Cristian, but it is just a (remarkable!) coincidence, because if I run it again I get a different number (2895.244). Are you sure you didn't run it for 10,000,000 runs?
Your minimize statement fails for me, but I haven't investigated why.
Edit: If I try N=10,000,000 it fails because runif throws an error.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
True,
I also get slightly higher values at subsequent runs of the calculation in that file. And almost always they are higher than 2895 (hence also larger than the initial value of 2894.493).
I initially also though Luc might have run it for 10 million times and I tried the 10.000.000 number of runs but it fails with the "incorrect range for variable at index #2" error.
Cristian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So use simulated annealing rather than Monte Carlo ![]() . It's also luck, but it is luck with the odds very heavily stacked in favor of finding the global minimum.
. It's also luck, but it is luck with the odds very heavily stacked in favor of finding the global minimum.
Of course, I am also biased ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
By all means, I am not ruling that out at all!
I am just weighing my options. And now I have the difficult task of choosing which on the "correct answer" is.
Apart from not being mathcad proficient, I am also not a mathematics guru (as a matter of fact I heavily hated maths all throughout primary, secondary, high school and university. It is ironic that I now tend to use maths more than my colleagues, in the form of Mathcad!)
Regards,
Cristian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And now I have the difficult task of choosing which on the "correct answer" is.
Well, Werner was the first to find the global minimum. Everything after than either verifies it or is a faster way of getting there, but they do not change the answer.






