Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Multiple Array results
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Multiple Array results
HI,
Please help. What is wrong with this. I am expecting to have a multiple array in the result .

Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Lex,
your Array dimensions don't match.
It should be like that:

Volker
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Dear Volker
Not like this I expecting 3 horizontal array and 5 vertical array . I need and result like this.
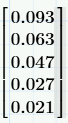
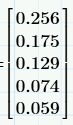

How I will get this in programming ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah! Ok.
can you attach the file please? (use advanced editor on the right top of the editor)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Do you like the following solution?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
yes. Thank you very much.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
I just miss this . thanks I got it right now.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
In matrix algebra (which is a noncommutative algebra), division is not defined. The division becomes the product between one of the two matrices and the inverse of the second one.
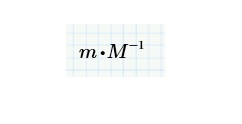
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Can you please send me the file. Its raise to the -1 ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
endeed, You should illustrate what you want more clearly. Given the above, you can create a program that does all the desired operations between the elements of the two vectors.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to do this in a programming ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
it isn't clear what you wont. m/M is a mistake. We can divide, for example, each element of m by each element of each column of M.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I guess, he needs something like this.

MH
Martin Hanák
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I was referring precisely to this.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The result should be in one box of matrix or array . I will give more detail tomorrow . thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That is a generic illustration of the product of a matrix for the inverse of another.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can do it without programming:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
How about this case ? What did I miss here ? Thank you in your support.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
your M is matrix !!!
MH
Martin Hanák
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the first problem you sent M was a single column, a vector. The elements of M could be addressed by a single index, so M_j made sense.
In this second problem M has three columns, so we need two indices to address an element. So M_j doesn't make sense.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What kind of output would you expect in that case? Following the logic of your initial question it would be a three dimensional array!
I wished that multidimensional arrays would be implemented in Mathcad but unfortunately they aren't. So the best you could come up wiith is a workaround with a 7 x 1 matrix whose components are 7 x 3 matrices so you get the 147 values you are probably looking for. As an alternative we could create a 7 x 3 matrix whose components are 7 x 1 vectors.
And if m is a two dimensional matrix, too -> the result could be a 2D matrix with 2D matrix elements, simulating a fourdimensional matrix.
Before you ask how to implement what you want you should first make clear what exactly a vector divides by a matrix should mean and how you would like this operation to be defined.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I seen multiple array are more complicated. I prepared not to used it , instead I will follow the single column and single index to make my life easy. Thanks. ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is yet another method to achieve the same effect.
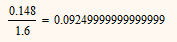
Prime seems to have an erroneous rounding method! The value at the upper left, 0.148 / 1.6 is exactly 0,0925, so rounded to 2 decimals it should read 0,092 as is the case in Mathcad 15 and below and NOT 0,093 as Prime is showing.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmmm! I always thought that 5's always went up, so 0.0925 would go to 0.093.
A short search reveals:

According to that rule 0.0925 should round to the nearest "even" number, 0.092.
Prime isn't consistent:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
> Hmmm! I always thought that 5's always went up, so 0.0925 would go to 0.093.
And you are perfectly right! I don't know where I had my mind when I wrote that it should be 0.092 (sure had not the IEEE rules in mind) !
I don't think that Mathcad 15 sticks to the rounding rules you are pointing to - it goes up at 5
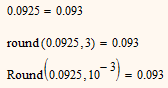
The reason for rounding down is simple rounding and conversion (dec to binary and back) errors.
and at 4 its rounded down.
Its interesting that Primes numerics seem to be different and less erroneous than Mathcads in this case.
The inconsistency you noticed may stem from the way the symbolic "float" works. Its not just rounding the end result - it just uses less digits for the whole calculation. But I am not sure where an how the significant digits are cut off. Sure not from the very beginning as otherwise we should see the result as 0.15/1.6=0,094






