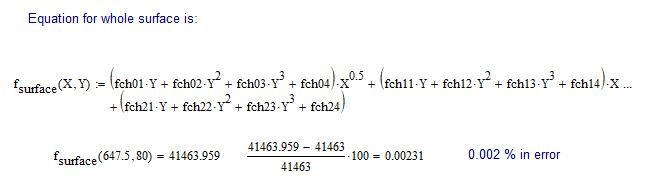Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Multivariable Regression, Curve Fitting & Surface Plots
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Multivariable Regression, Curve Fitting & Surface Plots
Hello,
I'm looking to reduce a dataset of 25 points to a surface curve fit. An older program (and required to be used) generated the points in question. Rather than spending many more hours on input the values, I was hoping to get a curve fit to the equations. Two variables of distance (x) and elevation (y) provide and output of heatflux (Q). I'm looking to essentially extrapolate the data into a large portion of points that will undergo more transformations pending the target geometry.
However, I'm unsure how to appropriately reduce the data. There isn't any issue with generating a x^3 curve for more than 3 points of data (as I've done before), but I'm seeming to be inputing something incorrect into MathCAD for trying to reduce the data to an appropriate approximation.
In addition, if somebody knows a way to accomplish this task in excel, that would also be benificial (though I question if excel has that power built into it).
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
You mention 'extrapolation'. For this you are best to get the equation of the surface.
This is an entirely different approach to the problem I have used professionally to determine the underlying mathematics on a surface in heating and cooling mills in plants.
It involves determining the equation that matches the surface in one direction say the X direction. Same equation but different coefficients at each Y position. Usually can be done with three coefficients in the equation.
Next you find an equations for the variation of these coefficients in terms of the Y direction. Again only three coeffficients are necessary for each coefficient.
See mathcad sheet for how it is done.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
P.S., if anybody knows how to get multiple files uploaded that would also be great. I keep getting a file 'type' being incorrect. (Guess it doesn't like mcdx and xmcd files?)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
May be this will be any help forvyou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime with Excel
See too
The chapter 1 from the book @Thermalengineering studies with Marhcad, Excel and Internet
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I was able to utilize the 'solver' within excel to reduce to a local minimum based on a least squares approach (as compared to a chebeshev approach). I've attached the file here for reference.
(For some reason my work computer didn't solve this but I was able to get it solved on excel 2016 at my home computer).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is helpful to reproduce the curved surface, but doesn't provide the coefficients for the equations. I'm looking to grab the coefficients so they may also be entered into other programs.
However, this approach is great to grab data from a dataset or run feed a dataset to the function and get the resultant parameters out. I would probably use this approach for the output from a user input where the data is some property table or other similar set.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
hi,
multiple files can be placed in a zip file then upload the zip file.
windows can do this.
cheers
terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
First the zip file enclosed has two files, that is how you upload multiple files.
Mathcad is capable of creating a cubic spline surface through a number of points in 2D. A condition of this is same number of points in each direction. Supplied data has 5 rows and only four columns. It is necessary to create 5 evenly spaced points in the Y direction.
This can be done by fitting a cspline through each row of Q and interpolating the 5 evenly spaced Y points.
Once we have same number of data points in both X and Y direction can use the 2d version to interpolate the surface for a 2d point.
Values on the cspline surface can be found by 2d interpolation and one point is shown.
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
For some reason when I input those values into the curve function into excel and compare those values to the ones put out by MathCAD, it seems to not pair up accuarately. I've attached my spreadsheet for reference. (I did expand to a xyy, xxy, xxx, yyy equation and the difference was minimal).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
to be complete need to answer if Excel can do it.
It can do linear interpolation in two directions.
http://www.engineerexcel.com/bilinear-interpolation-excel/
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
You mention 'extrapolation'. For this you are best to get the equation of the surface.
This is an entirely different approach to the problem I have used professionally to determine the underlying mathematics on a surface in heating and cooling mills in plants.
It involves determining the equation that matches the surface in one direction say the X direction. Same equation but different coefficients at each Y position. Usually can be done with three coefficients in the equation.
Next you find an equations for the variation of these coefficients in terms of the Y direction. Again only three coeffficients are necessary for each coefficient.
See mathcad sheet for how it is done.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much to everybody for the answers. It makes sense and I'll be able to expand on the MathCAD documents and implement in excel (as needed) for value outputs.
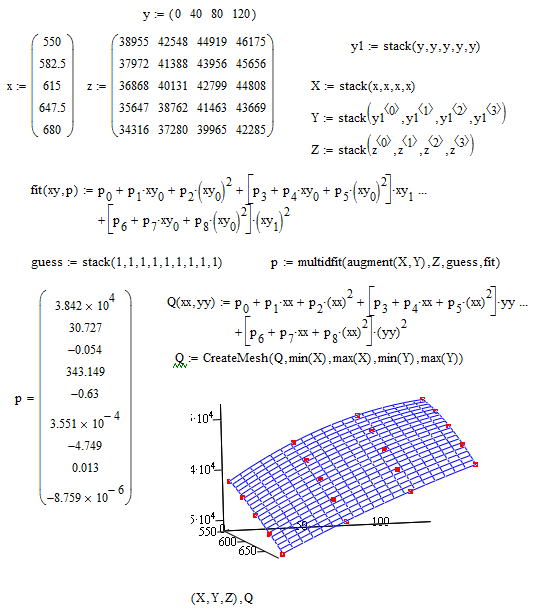
I did alter the numbers I used to a format of: Q = (a + b*x + c*x^2) + (d + e*x + f*x^2)*y + (g + h*x + i*x^2)*y^2
The equation fits the original data with less than a 0.05% error, which is pretty good.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
one more approach. In the original Excel sheet written at the bottom is a function for Y in terms of
seven coefficients c,a1,a2,a3,b1,b2,b3. in terms of x1 and x2.
Y = c + a1*x1 + a2*x1^2 + a3^x1^3 + b1*x2 + b2*x2^2 + b3*x2^3.
It is possible to create seven equation to determine the seven coefficients.
The resulting surface is not as close as the previous post where the form of the equation is guessed as a fit to the data.
Regards
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Obtain a good fitting equation in both directions for the surface given to 0.02% or closer is enclosed.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Here is the calculation of the surface in Excel using the formula found in MathCad


![1-1[1].png 1-1[1].png](https://community.ptc.com/t5/image/serverpage/image-id/2510iD493BA126F74FC80/image-size/large?v=v2&px=999)