Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Narrow band plot(dB vs linear frequency) to 1/3 Octave band plot(dB vs 1/3 Octave band) with Prime 4
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Narrow band plot(dB vs linear frequency) to 1/3 Octave band plot(dB vs 1/3 Octave band) with Prime 4
Hello to all expert Mathcaders 🙂
I have to preface my question by saying that I am a newbie in the whole field of acoustics. I am however an expert in structural analysis. So please answer my question keeping in mind that fact. I now find myself in a situation where I have to determine the structure-borne sound/sound transmission characteristics of rubber structures. With the aid of harmonic analyses, I can determine the sound transfer function (in dB) and the so called transmission loss (also in dB) of the these structures. I can then make plots of for example transmission loss (in dB) versus frequency (Hz). However, the x-axis, which is the frequency is a linear distribution of the frequencies which corresponds to the frequencies as derived from the harmonic analysis. So let us say I performed my harmonic analysis for a frequency range from 0Hz to 500 Hz at intervals of 1Hz. That means that I have 501 result points for the frequency and the determined values of the transmission loss (in dB). I now make a plot of the transmission loss vs the frequency in excel, the frequency axis (horizontal) being logarithmic and the transmission loss on the vertical axis. So far, I get good curves which correspond to my expectation, when I use the mentioned methodology.
However, any one who has the slightest idea in sound analysis or machine acoustics, knows that my above representation could be characterized as a so called narrow band (Please correct me if I am wrong with this denotation but that is what I have gathered, speaking to some experts). Acoustic engineers generally however want the frequencies to be represented in a 1/3 Octave Band. My limited understanding of the 1/3 Octave Band is that it has to do with some kind of summing or averaging of the frequencies depending on the outcome that is needed and the results present that need to be analyzed. I may not know exactly what the 1/3 Octave band is all about but I know that I am required to present my results of, for example transmission loss (in dB) vs frequency (Hz and log scale) on a plot that is transmission loss (in dB) vs frequency (in 1/3 Octave band scale).
I will love to do this in Mathcad Prime 4.0 but have no idea how and where to start or if this is at all possible in Mathcad Prime 4.0. I do however know that it is possible to get the plots I need using some kind of Matlab code and acoustic engineers are fond of using Matlab for this "Octave band analysis". I will therefore be grateful if some Mathcad Prime expert can help me achieve the desired plot in Mathcad Prime 4.0, if it is possible to be achieved at all.
PS: If someone is kind enough to help, the person can basically use any set of data for the transmission loss and the frequency, But if that is not possible, I could provide some trial values which could be used for the help. Assuming that all of this possible in Mathcad at all.
Thanks very much and looking forward to your feedback.
- Labels:
-
Mechanical_Engineering
-
Programming
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi jmebara,
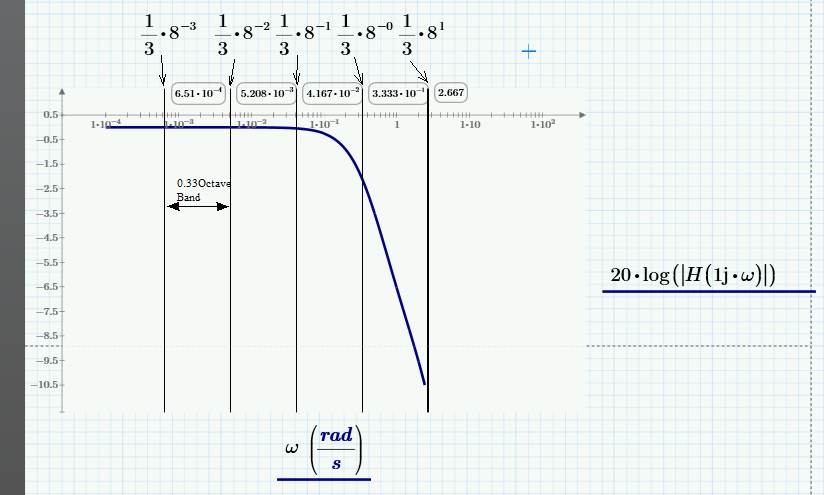
The following is an example of a Bode diagram of the transfer function of a system, in which the 1/3 octave bands are highlighted:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi MF.
Thanks very much for your quick response. First of all, the plot of the transfer function in dB vs frequency (log 10 scale), which you have posted is similar to the kind of plots that I am trying to analyze. So that's the right direction 🙂 Thanks for also highlighting the octave band regions. Gives me a visual depiction.
If I understand what you have shown, the Sound Levels of the transfer function in each 1/3 Octave band have to be summed up (or averaged?) to the maximum frequency based on the definition of the 1/3 Octave band filter? i.e. some kind of spectral analysis? As I said in my post, I do know some acoustic engineers who have written codes in Matlab for 1/3 octave band filters which they use for such spectral analysis (if that is what it is called). As I have seen on some Websites while doing some Research (e.g. here http://www.sengpielaudio.com/calculator-octave.htm), such summing up gives rise to some kind of "bar Chart" (if I could primitively call it as such) with the bars located at the center frequency of the 1/3 octave band. The Matlab codes I have seen however create a smooth line x-y plot and not just a bar Chart.
The big question is how do I transform the bode plot (e.g. the one you have posted) to such a smooth line x-y plot of transfer function sound Level vs frequency (1/3 octave band)? Is there some Kind of code that can be written to create 1/3 octave band filters which can be used to automatically generate the requeired plot? It is probably a challenging task to do this in Mathcad and I am not a good programmer to know how to achieve what I wish in Mathcad. Hoping that someone who is good at this can help me to achieve this in Mathcad.
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi MF.
(I just posted a reply and it seems it was deleted. Probably because I added a website. So I will post the reply again without the website which I referenced)
Thanks very much for your quick response. First of all, the plot of the Transfer function in dB vs frequency (log 10 scale), which you have posted is similar to the kind of plots that I am trying to analyze. So that's the right direction 🙂 Thanks also for highlighting the octave band regions. Gives me a visual depiction.
If I understand what you have shown, the Sound Levels of the Transfer function in each 1/3 Octave band have to be summed up (or averaged?) to the maximum frequency based on the definition of the 1/3 Octave band filter? i.e. some kind of spectral analysis? As I said in my post, I do know some acoustic engineers who have written codes in Matlab for 1/3 octave band filters which they use for such spectral Analysis (if that is what it is called). As I have seen on some Websites while doing some Research (e.g. check the website sengpielaudiocom under the topic Adding decibels of one-third octave bands to level of one octave band and vice versa), such summing up gives rise to some kind of "bar Chart" (if I could primitively call it as such) with the bars located at the Center frequency of the 1/3 octave band. The Matlab codes I have seen however create a smooth line x-y plot and not just a bar Chart.
The big question is how do I transform the bode plot (e.g. the one you have posted) to such a smooth line x-y plot of Transfer function Sound Level vs frequency (1/3 octave band)? Is there some Kind of code that can be written to create 1/3 octave band filters which can be used to automatically generate the requeired plot? May be this is not so easy to achieve in Mathcad and I am not such a good programmer to know how to achieve this goal in Mathcad but I will be very grateful if some Mathcad expert could help me to achieve this in Mathcad.
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi jmebara,
in general the more the question is synthetic and clear, the better it is.
You could add some photos to make the topic clearer (using for example the Stamp button (display), cut and paste in paint), and then it's not even clear what the filter is. Perhaps you are referring to a very narrow bandpass filter that is a filter with pass band one third of an octave?
If we consider that the system, through which the sound wave propagates, is linear and stationary then, the system response, in the frequency domain, is given by the product of the system transfer function by the Fourier transform of the signal placed at the entry of the system. The system behaves like a frequency filter. It could be high pass, low pass, band pass and stop band or notch .....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi MF,
Good Point. Let me add some pics to see if I could make the question clearer.
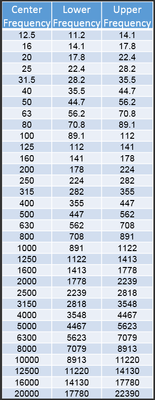
According to one blog I visited why researching the following is described: "In Engineering applications, sound spectrums are usually represented in octave or one-third octave frequency bands rather than in narrow frequency bands. This frequency representation is linked to the perception of sound by a human ear and it allows a compression of the amount of information. An important part of the information is however lost when converting results from narrow frequency bands to octave or one-third octave frequency bands." The frequencies of the 1/3 Octave bands are as follows:
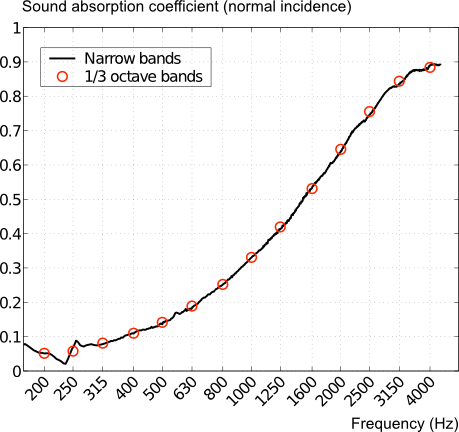
As an example on the blog, the following curve is shown which depicts the results of the conversion from narrow band to octave band with both curves plotted. In this example however, they are dealing with the sound absorption coefficient for a fibrous material. Also, Matlab was used:
% function [one_third_freq,band] = one_third_octave(frequencies,measurements)
%
% Narrow bands to one-third octave bands representation.
%
% Example: [one_third_freq_preferred,band] = narrow_to_one_third_octave(frequencies,alpha_diffuse)
%
% The input parameters are:
% o frequencies: frequency values
% (with a fixed of variable frequency step),
% o measurements: acoustic absorption coefficent values
% (corresponding to the frequency vector defined above).
%
% The output parameters are:
% o one_third_freq: center frequencies of 1/3 octave bands,
% o bands: values of the acoustic absorption coefficent in 1/3 bands
%
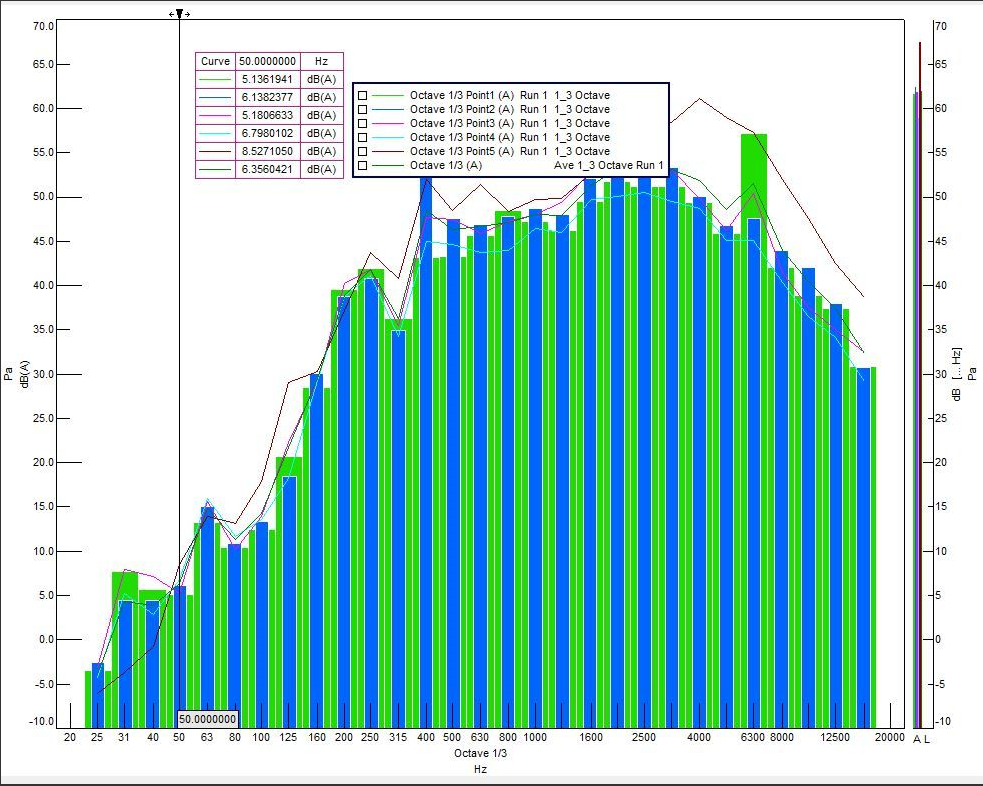
A plot which Shows what I am trying to get at can be seen in the following Picture which is an example of Sound pressure Level vs frequency (In the Picture, the narrowband is not depicted. It seems to have already been summed up or averaged to obtain the results in 1/3 Octave bands):
As you can see, the 1/3 Octave bands have been assessed and a smooth line plot has been created.
I would like to do something similar in Mathcad in which I get as final results the smooth line plot.
The following is a Matlab code to convert narrowband to 1/n octave band...These are some of the stuffs I have found while checking out how to do this whole Thing. I haven't personally tried out the following Matlab code. I will just be happy if I can do all this in Mathcad :):
%Program to convert narrowband data to 1/n octaveband data. Just send it an
%array of band center frequencies, the dB values to sort, and the nth
%octave band you want. This can be used with any dB values (e.g. Sound
%pressure level (SPL), sound power (Lw), sound intensity (Li), etc..
%
%Important Note 1: The given center frequencies must be a constant df apart
%
%Important Note 2: If your data was windowed during the FFT process and you
%used the amplitude correction factor (ACF), then you need to adjust your
%data to the energy correction factor when converting to octave spectra. See
%the first couple lines of the function to adjust this.
%
%-Examples:
%[sortedData,Fc,Flow,Fhigh] = NarrowToNthOctave([490,510,500],[60,60,60],1)
%[sortedData,Fc] = NarrowToNthOctave([490,510,500],[60,60,60],3)
%[sortedData,Fc] = NarrowToNthOctave(freqArray,dBArray,3)
%
%-V4 TMB 12/1/2015
function [sortedData,Fc,Flow,Fhigh] = NarrowToNthOctave(arrayOfNBCenterFreqs,arrayOfdBToConvert,n)
df=arrayOfNBCenterFreqs(2)-arrayOfNBCenterFreqs(1);
%Use correctionFactor=1 if you did not window or you used ECF
correctionFactor=1;
%Use this if you used a hanning window with ACF
% ACF=(1/mean(window(@hann,1028));
% ECF=(1/mean(window(@hann,1028));
% correctionFactor=ECF/ACF;
data=data*correctionFactor;
%Determine Initial Center frequency (Fc)
previous=1000*2^(1/n);
lowFc=1000; %Start at 1000 Hz and find lowest Fc
while (previous-lowFc) > df
previous=lowFc;
lowFc=lowFc/2^(1/n);
end
%Compute center frequencies
ii=1;
Fc(ii)=lowFc;
while Fc(ii) <= max(arrayOfNBCenterFreqs)
ii=ii+1;
Fc(ii)=2^(1/n)*Fc(ii-1);
end
%Compute high, low frequencies, and bandwidth (BW) from center frequencies
Flow=Fc/sqrt(2^(1/n));
Fhigh=Fc*sqrt(2^(1/n));
BW=Fhigh-Flow;
%Sort data in frequency bins
sortedData=zeros(1,length(Fc)); zeroFreqValue=0;
for jj=1:length(arrayOfdBToConvert) %Do for each value given
for kk=1:length(Fc) %Check each Fc bin to see where value should be placed
if arrayOfNBCenterFreqs(jj)>=Flow(kk) && arrayOfNBCenterFreqs(jj)<Fhigh(kk) %Find place. In the rare case a given center freq = flow(ii)/fhigh(ii+1) then sum the value in flow
if sortedData(kk)==0 %if no values has been added to the band then set initial value
sortedData(kk)=arrayOfdBToConvert(jj);
N(kk)=1;
else %else sum in the value
sortedData(kk)=10*log10(sum(10.^([sortedData(kk) arrayOfdBToConvert(jj)]./10))); %dB add value to that bin
N(kk)=N(kk)+1;
end
else %else check to see if the value belongs in the 0 Hz band
if (kk==1) && arrayOfNBCenterFreqs(jj)<Flow(kk)
if zeroFreqValue==0
zeroFreqValue=arrayOfdBToConvert(jj);
else
zeroFreqValue=10*log10(sum(10.^([zeroFreqValue arrayOfdBToConvert(jj)]./10))); %dB add value to that bin
end
end
end
end
end
%Apply bin correction factor for when center frequencies are not integer
%multiples of the bandwidth (BW)
for ll=1:length(N) %Look through each bin that had values added to it
if (N(ll)~=0) && (floor(BW(ll)/df)<=N(ll)) %If values were added and there are enough values added to make applying the correction appropriate then apply correction
sortedData(ll)=sortedData(ll)+10*log10(BW(ll)/(df*N(ll)));
end
end
%If DC value was given, add to sorted array
if zeroFreqValue~=0
sortedData=[zeroFreqValue sortedData];
Fc=[0 Fc];
Flow=[0 Flow];
Fhigh=[0 Fhigh];
end
%Remove unused bins at beginning if only higher freqs were given
removeThisMany=0;
for ll=1:length(sortedData)
if sortedData(ll)==0;
removeThisMany=1+removeThisMany;
else
break
end
end
sortedData=sortedData(removeThisMany+1:end);
Fc=Fc(removeThisMany+1:end);
Flow=Flow(removeThisMany+1:end);
Fhigh=Fhigh(removeThisMany+1:end);
%Remove bin at end if unused
if sortedData(end)==0
sortedData=sortedData(1:end-1);
Fc=Fc(1:end-1);
Flow=Flow(1:end-1);
Fhigh=Fhigh(1:end-1);
end
end
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I think that all the members of the community are willing to solve small problems that arise with mathcad, no one, however, wants to deal with an extended project, only for the good of humanity ........
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
😄 Again good point 🙂 It's no prob if this seems too big for the community or impossible to realize with Mathcad. I have been able to run some Matlab codes that can do it for me. But I don't use Matlab for my engineering calculations. Only Mathcad. So I thought it will be possible to just do everything in Mathcad. It might seem more complex the way I am explaining it than how it actually is. I will guess that if someone is familiar with acoustics, filters, octave bands and spectral analysis, they can easily see what I am trying to do and the only question is if one can program these octave band filters easily in Mathcad to generate the bode plots in 1/3 octave bands. Thanks for your kind feedbacks though 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
... I would like to add that PRIME is a software still in gestation, ie it is very limited, especially for graphics, compared to mathcad 15 which is, by far, even higher than matlab in some cases. Indeed, someone believes that PRIME has a very uncertain future. Therefore, it would be convenient to use mathcad 15 ...Including me, here are a lot of people who are experts in analog and digital electronic filters, maybe a little less in acoustics. Wait for the intervention of others. Greetings.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That will SUCK big time if PTC is not able to take PRIME to where Mathcad 15 was and beyond but rather abandon the software. That will truly suck big time. Few years ago when I posted my first question here, I was using only Mathcad 15. The company I work for was also only using Mathcad 15, however we had started a complete transition from 15 to Prime. At the moment, the company strongly insists that all engineers use only Mathcad Prime. So we have completely moved away from Mathcad 15 at the company, even against the will of most engineers. I have had to navigate through all the troubles in Prime and I am just trying to make the most of what Prime offers now...Still miss the beauty that is Mathcad 15 especially its robustness. However the IT administrators at the company cited the lack of support and update of Mathcad 15 from PTC as the main reason for the complete transition. As well as the fact that PTC insisted that Prime is where the future lies and where they will put in all their effort. So it will come as a shocker for my company and most companies I know if Prime is suddenly abandoned. Anyways, we'll see. Yeah, I will be waiting for intervention by others. Regards 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's not impossible to realize what you want in Mathcad.
Mathcad (real Mathcad as well as Prime), is capable of dealing with (virtually) any problem that can be described mathematically. And your problem appears to be a couple of math operations on the output of a DFT. Mathcad can do the DFT as well, so you could even feed it a recording of a response on (white) noise to finally arrive at a plot of responses in whatever fraction of octave bands. It just takes one knowledgable on Mathcad (or Prime) AND on the subject/topic of acoustics.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Luc for the response. I remember you were the one who gave me a comprehensive answer to my first question on this forum.
I am still waiting for the ONE who is that familiar with Mathcad/acoustics. I am fully confident that it is possible to achieve this in real Mathcad or Prime. Just not sure how to go about it.