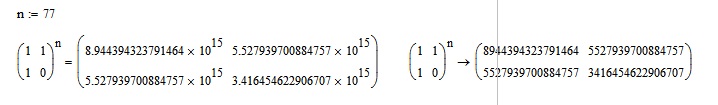Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Natural Number and Sum of Fibonacci Numbers.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Natural Number and Sum of Fibonacci Numbers.
Hello, Everyone.
My question :
Thanks in advance for the time and help.
Best Regards.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, to round it off find attached my second version of the decomposition program. Its faster and more versatile and I'm a bit happier with it but still have the feeling that its far too complicated and cluttered.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Do want confirmation there is, or is not, a solution? Or a solution? Or some tips that will help you find (or find there isn't) a solution?
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I greatly appreciate your response, Stuart. On my side, I would want one of any of them.
Best Regards.
Loi Le.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
May be this help you:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A "little" bit faster using Moivre-Binet. The "round" should not be necessary but is because of floating point rounding errors of the numeric processor in Mathcad. But even then the numeric result is wrong for n>70 - use symbolic eval to get the correct result.
BTW, usually Fibo(0)=0 and Fibo(1)=Fibo(2)=1.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
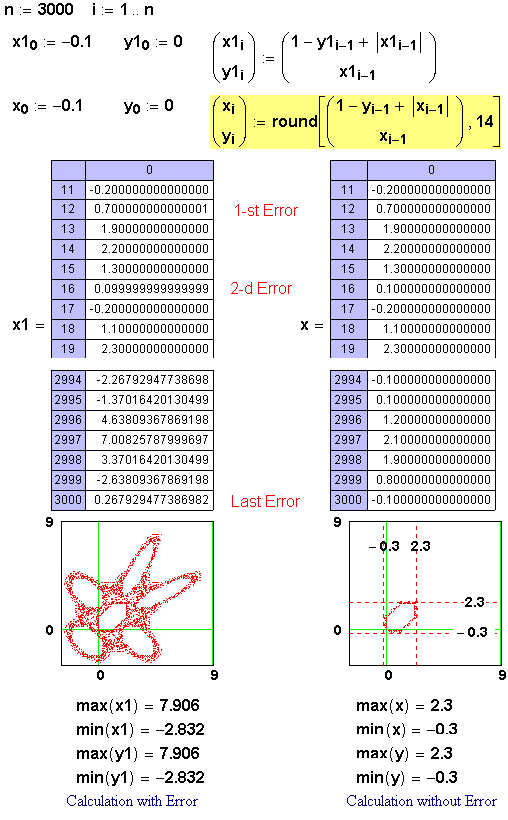
Werner Exinger wrote:
A "little" bit faster using Moivre-Binet. The "round" should not be necessary but is because of floating point rounding errors of the numeric processor in Mathcad.
One good example of the round using:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery, thats interesting. I was aware of numerical errors using the expression I posted with square root of 5 and division, but I would not have expected those numerical errors to occur in the simple operations in your example.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
... or avoid the rounding issue for a little longer by matrix exponentiation ...
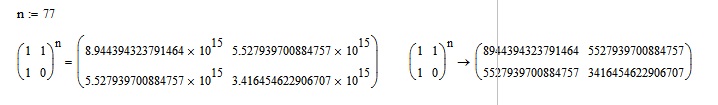
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK.
1. A solution exists.
2. Assuming you want to have a go yourself, then I won't give the answer but I find it amusing that (when I reversed the possible list of Fibonacci numbers) 5 of the indices of the solution vector were themselves Fibonacci numbers.
3. If you want to have a go, then there are a couple of relatively straightforward ways but both of them are somewhat brutal ... one of them may possess slightly more finesse than the other as it is easier to generalize.
a. Generate a list of Fibonacci numbers up to the maximum possible Fibonacci number.
b. Using nested for loops, create a table of all possible sum then search for the desired sum - alternatively, just return when you've found one.
c. Create a vector the same length (n) as the Fibonacci list, then 'binary count' it from 0 to n-1, multiplying the vector by the Fibonacci list until you find the solution.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
c. Create a vector the same length (n) as the Fibonacci list, then 'binary count' it from 0 to n-1, multiplying the vector by the Fibonacci list until you find the solution.
Would have to count from 0 to 2^n - 1 (in our case 2^37 - 1), or am I missing something?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
c. Create a vector the same length (n) as the Fibonacci list, then 'binary count' it from 0 to n-1, multiplying the vector by the Fibonacci list until you find the solution.
Would have to count from 0 to 2^n - 1 (in our case 2^37 - 1), or am I missing something?
You would ... except you can examine the range of possible values and limit searches to those.
Or you could cheat and simply start taking a Fibonacci number from 20121221 and a Fibonacci number from the remainder and so on ... which would reduce the number of combinations to check in a (brute-force tailored brute-force solution) from three or so million to 8 subtractions.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Would have to count from 0 to 2^n - 1 (in our case 2^37 - 1), or am I missing something?
You would ... except you can examine the range of possible values and limit searches to those.
That could explain why my solution seems to run "endless" 😉 At least with the original posters sum of 20121221 as it seems to work using smaller sums. I wrote a function with 2 parameters (expected sum and number of fibo numbers). That way I could not use nested loops. If I would allow to use a fibo-number more than once it would even get worse.
How long took your program to come up with one (all?) solution?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Would have to count from 0 to 2^n - 1 (in our case 2^37 - 1), or am I missing something?
You would ... except you can examine the range of possible values and limit searches to those.
That could explain why my solution seems to run "endless" 😉
Indeed it would explain it! ![]()
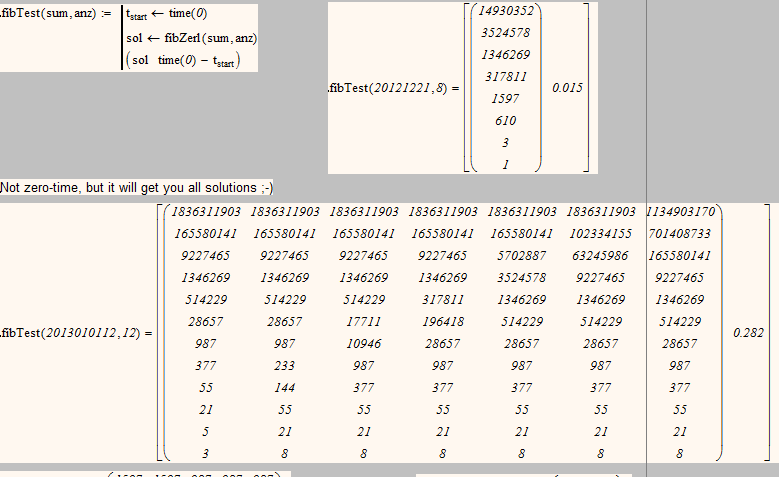
I have a brute force solution (nested loops) that takes around 5 1/2 seconds to perform roughly 3 million iterations before coming up with a solution.
However, if you get a little frustrated then there is a much simpler method that returns a result in less time than the time function can distinguish.
Stuart

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Impressive and inspiring. So I have something to think about. Guess you used the "cheat" (as you called it in a prior mail) and your program stops when it finds the first solution - not trying to go for all solutions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Impressive and inspiring. So I have something to think about. Guess you used the "cheat" (as you called it in a prior mail) and your program stops when it finds the first solution - not trying to go for all solutions.
Well, the brute force method stops when it finds a solution but the "zero time" algorithm uses a completely different method and takes a total of 8 operations.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, I've found the solution your zero-time algorithm has found (sum of the fibo-indices is 166 if the series begins with fibo(0)=0 and I take 2 as the index for the 1). But I don't think that subtracting the highest possible fibo-number is a suitable general algorithm and its kind of luck that the number of summands is eight in this case. With a sum of 20121230 you arrive at only seven summands (you could split any of the seven numbers in the two precedings of course to end with a sum of eight numbers). Think we agree that we dont use 0 as a fibonacci number in this task and we do not allow two 1's. According to your saying about 5 indices being fibo-numbers in a reversed vector thats only the case if your vector begins (or ends) with the "second" one, that is the fibo series being 1,2,3,5,... and the 1 being vector element 34.
Still working on a more general function if I find some time to do so.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So I finally created a program which finds all decompositions for any given number of Fibonacci numbers.
Its a single function which is called recursevly - so not zero-time. I am not really happy with my totally cluttered program. If I find some time I will have to go over it again. In particular the way I did remove duplicates is aweful. I attach the worksheet with the function hidden in a locked region so everybody is still free to have a go on there own. On the other hand I sometimes read here that this regions aren't save and can be opened without knowing the passphrase - is this true? Anyway, I don't care in this case.
A nice follow up would be a function for the Zeckendorf representation of any number. According to a theorem by Zeckendorf any positive integer can be written in a unique way as the sum of one or more different Fibonacci-numbers in such a way, that this decomposition does not include a pair of consecutive Fibonacci numbers. As I understood the theory the greedy algorithm (Stuarts zero-time, as I guess) will do the job here.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello, again.
I greatly appreciate all of your time and help. And I have a related question :
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello, again.
I greatly appreciate all of your time and help. And I have a related question :
Glad to be helpful.
Concerning your new question I think you already know, that Given and solve won't do the work but and you have to write a small program. Maybe you would like to post a worksheet to show what you have attempted so far and someone may give you a hint why it didn't work.
On the other hand, you already have half of the solution by using my worksheet. The second half (the six Pell numbers) could easily be found (even "manually") with the greedy algorithm using a list with the first 12 Pell numbers. Both parts of the solution are unique.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks, Werner. Following up your instruction above, "the second half (the six Pell numbers) could easily be found Manually using a list with the first 12 Pell numbers" :
"Both parts of the solution are unique": I think I need being helped with this with brief explanation.
Thanks again,
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks, Werner. Following up your instruction above, "the second half (the six Pell numbers) could easily be found Manually using a list with the first 12 Pell numbers" :
"Both parts of the solution are unique": I think I need being helped with this by brief explaination.
Don't think so as you have already found the solutions, as I see. You found the six Fibonacci numbers by using my program and as you can see its the only way to split 20120 into exactly six different Fibonacci numbers (otherwise my program would have listed more solutions), so that was meant with unique. By manually I meant without writing a program: looking in the list of Pell numbers (you need the first 12 as the 13th is greater than 20120), picking the greatest possible (greedy) as the first, calculate the difference, looking for the next possible Pell number and so on until you arrive at zero. Luckily enough you end up with exact six numbers, as disired. Looks to me like you have done just that as you didn't wrote a function pelZerl().
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Do you know fine Fibonacci Numbers:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, to round it off find attached my second version of the decomposition program. Its faster and more versatile and I'm a bit happier with it but still have the feeling that its far too complicated and cluttered.