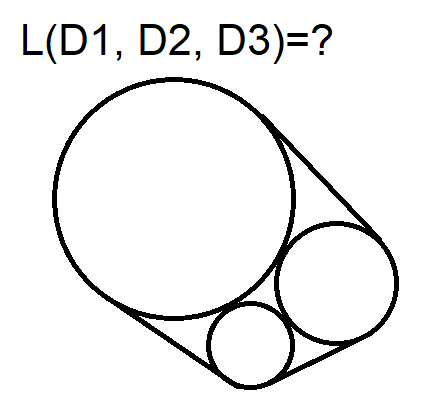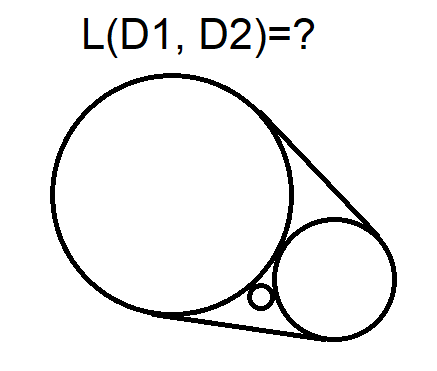Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
New problem with circles
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
New problem with circles
The belt pulls together two or three circles with D1, D2 and D3. What is the length L of the belt?
If D1=D2=D3 L=D*(3+pi)
See also
https://community.ptc.com/t5/PTC-Mathcad/Malfatti-circles/m-p/687281
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The mathematical model is easy to check. The kinetic energy, the potential energy of the raised middle can and the potential energy of the stretched rubber band will change as our pendulum oscillates - it will change from one form to another, but their sum must remain constant. This does not take into account the loss of energy due to friction.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If the elastic is very hard, then the central ball can fly into... space.
There was such an anecdote.
The Chinese have launched a satellite of the Earth. 100 million people were holding a slingshot, and another hundred million people were pulling a rubber band.🤣
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In Russia, they often say this - this problem is so complicated that it cannot be solved without half a liter (a bottle of vodka 0.5 l).
Ahh, much more likeable than energy drinks! 🙂
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's stronger than vodka.
I used this in 1968-69 to blow up heaps of coal that died in the cold when I worked as the head of a boiler house in Kazakhstan.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner, Fred!
And what, my formula for determining the length of an elastic band is not correct? At first I calculated it through the betta angle, but Alan suggested a simpler formula.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Val,
Your equations aren't wrong! My first posting was wrong (which Werner pointed out.)
But your first equation
is only valid when the center cylinder is in contact with the ends (b < 60 deg) since it's Pythagoras' theorem and you need the distance between the centers to be 2r.
I think to solve the motions we need to look at the forces that develop. I'm working on it, but it may take a few days . . .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just a few thoughts:
I guess one problem could be that the force applied by the rubber band not only changes in magnitude over time but also the direction changes. Furthermore, as we don't consider friction, I think we will get quite unrealistic results if we don't consider friction between the pencils and the rubber band. Maybe one approach could be to assume that the part of the elastic which touches the pencils does not stretch at all and applies no force? But would it be correct to assume that the force is applied to the center of the circle?
If the weight of the pencil is large enough and the strength of the elastic small it may also be possible that due to inertia the outer two balls "shoot" out to the left and right only to be recaptured by the elastic moments later as my non-realistic animation tried to show. Same with the top ball shooting up not touching the two outer ones for a moment (beta>60°)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ignoring friction (while it will yield unrealistic results) will reveal the characteristics of the oscillator Val envisions, if it's there. The basic solutions for pendulums and weights on springs start by ignoring friction. Which equation below have you seen more often?
One thing that interests me is the effects of the mass of the cylinders and the strength of the elastic band, and their effects on the motion. If (for example) the elastic is very strong then the condition of minimum length will be the resting state. As the band gets softer and the cylinders heavier we would reach a point where the three cylinders all lie on the table surface. Is there a weight/strength relationship that would settle out at some intermediate angle?
Attaching my "in work" file (clearly not done!) for comment/correction.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You sure are right that omitting the friction is mandatory, at least in the first attempts. And it sure would be interesting to see if you can achieve the oscillation Valery expects.
But I wondered about how the tension in the whole rubber band would affect a single cylinder. Especially I am absolutely not clear about the effect the part of the rubber band around the circle would have.
In your sheet you make the down force on the upper circle dependent on the change of length of the whole rubber band and I wonder if its not just the part of the rubber band I sketched in red in the following pic (as you can see I am absolutely unsure about the arc part of it). The ratio of this part of the band to the full circumfence varies as the circles start moving.
Just some vague thoughts of someone with very limited knowledge in applied physics.
EDIT: Just read that a band of elastics would be different from a normal spring as its something like an entropic spring which stores its energy as thermal energy which is also the reason a rubber band gets hotter when its stretched ... ?? Does this mean that Hooke can not be applied? (https://www.quora.com/Which-force-is-used-for-stretching-a-rubber-band)
Hmmm, I knew it would be beyond me ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
All good questions:
"In your sheet you make the down force on the upper circle dependent on the change of length of the whole rubber band and I wonder if its not just the part of the rubber band I sketched in red in the following pic (as you can see I am absolutely unsure about the arc part of it). The ratio of this part of the band to the full circumfence varies as the circles start moving."
If we are ignoring friction (and I think we've agreed at least in first efforts,) then the elastic band can slide freely over the cylinders, and the tension in the band will be uniform along the band and related to the change in the total length.
"Just read that a band of elastics would be different from a normal spring as its something like an entropic spring which stores its energy as thermal energy which is also the reason a rubber band gets hotter when its stretched ... ?? Does this mean that Hooke can not be applied?"
Once again, you are correct. A rubber band is a poor spring. If you do an experiment you will discover that it has hysteresis, the loading curve is different from the unloading curve:
So we could find a different expression for the force/extension curve and even account for whether the band was expanding or contracting. But the assumption that it obeys Hooke's Law, like ignoring friction, is a good first approximation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Non linear Hooke
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for clarifying.
I am already looking forward to your further results in this matter (which we both said that we would not deal with further 😉 )
Actually I would have thought that the downward force resulting from the elastic on the top circle would be larger in the first picture below than in the second one (the total length of the rubber band is the same in both cases)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
" I would have thought that the downward force resulting from the elastic on the top circle would be larger in the first picture below than in the second one (the total length of the rubber band is the same in both cases)"
Once again you're right! The band exerts a tension force on each side of the central cylinder that's aligned with the band. So the vector sum of these two forces sums to zero in the horizontal direction and to a smaller value as b decreases. When the three cylinders align in a horizontal row the vertical force from the band is zero. (This is part of the reason why I'm not convinced that this arrangement will ever oscillate.)
(which we both said that we would not deal with further )
Yeah! Well, it's nice to have a discussion!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks again for the clarification.
I thought that reason that the force would be larger when the circle is higher up would be because the part of the elastic applying the force is larger (the tangent segment between upper and lower circle). But your argument rather is that its larger because the angle changes and so the vertical component gets smaller when the upper circle lowers. The tangent length does not matter because we assume no friction between the circles and the band. Makes sense to me, yes.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Fred_Kohlhepp wrote:
When I was a student, MPEI had the most modern electrical engineering classroom with TVs at that time. There was a note in the main newspaper of the USSR "Pravda". It was written there that the lecturer presses a button and a Hysteresis loop (with a large letter!) appears on the TV screen as if alive.
The lecturer became famous throughout the country, but many approached him and asked: "And how is old Hysteresis doing there?"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
New new problem.
Three cylinders of radius r are connected together in the form of a pyramid (see the Photo) and fit tightly into a pipe with radius R. The radius of the pipe begins to increase. How will the position of the cylinders in the pipe change? A variant of the problem: the cylinders are connected by an elastic band of different elasticity.
We can get an oscillator without a rubber band!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Pictures for new new problem. And Prime 6 in attch as the first step
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
New new new problem!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is it correct? Prime 6 and Mathcad 15 in attach!
- « Previous
-
- 1
- 2
- Next »