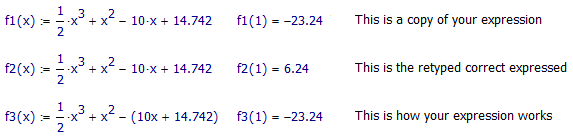Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Newton Raphson Method Help
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Newton Raphson Method Help
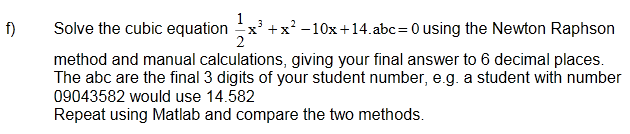
Hi I have started this, I don't know how to start this question, I haven't ever used the Newton Raphson method, the abc in my case would be 14.742. How would I go about solving this equation manually First of all?
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Are you sure you are allowed to use Mathcad? ![]()
Have you tried solving using the methods in your other thread.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No I have to use mathlab, but I need to solve it manually first![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Salim Ahmed wrote:
No I have to use mathlab, but I need to solve it manually first
That's a shame, however, have a look at my post above.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry the abc is 742 not 14.14.742 but it would be 14.742. Disregard the 14 already in there.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Salim Ahmed wrote:
Sorry the abc is 742 not 14.14.742 but it would be 14.742. Disregard the 14 already in there.
Just remove the first 14 and you have your answer. ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
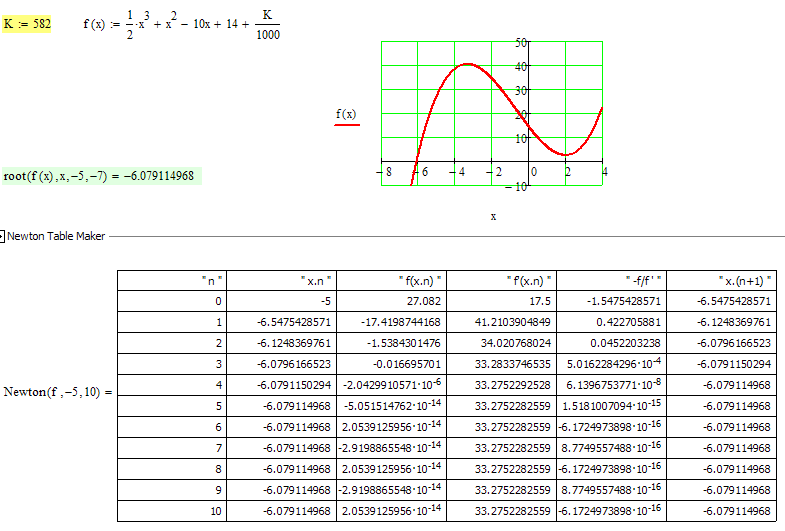
Just to get you started. What you are supposed to do is making a table like the one below - of course you should do it manually just using your calculator.
As you can see it does not take many interation steps until the difference between successive approximations is (much) smaller than 10^-6 and so the sixth decimal does not change anymore.
You see the approximations in the last column and they are then transfered to the second column for the next iteration step.
The first thing to do in that kind of task is to plot the graph of the function to get a decent start value for the iteration. In my case I had chosen -5 on purpose but sure -6 would have been a better choice.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What would the root be if k was 742? sorry its just I have not got mathcad at home just at uni.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
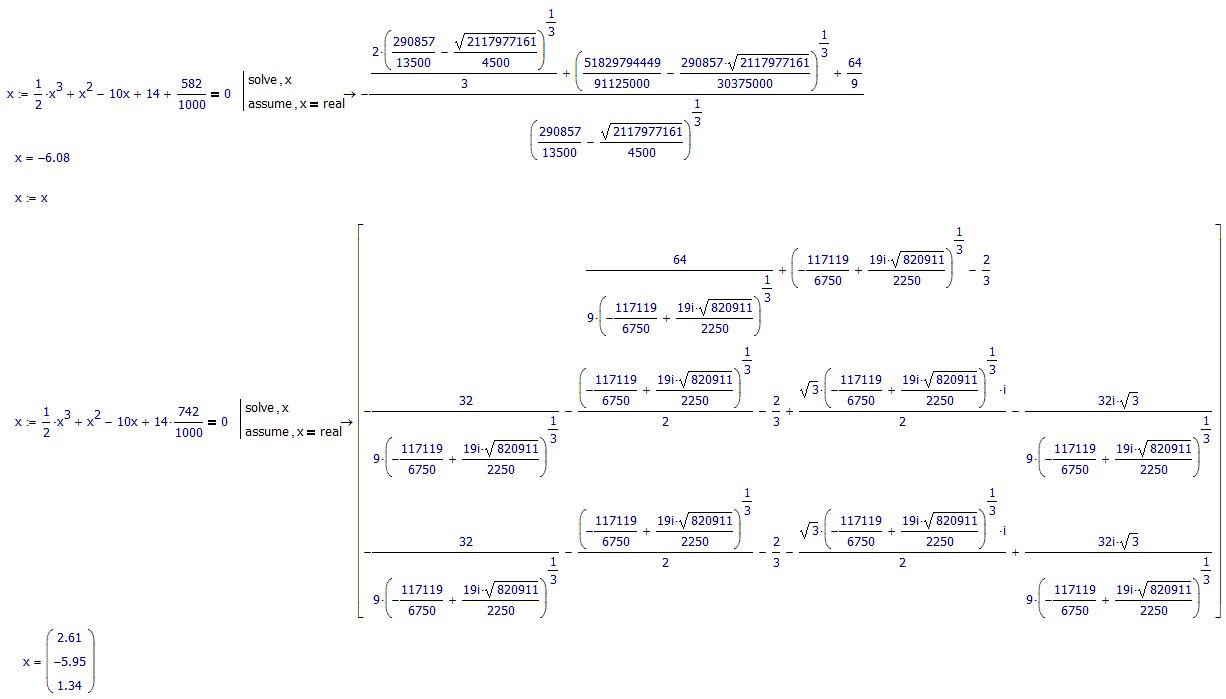
The symbolic processor finds three solutions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike Armstrong wrote:
The symbolic processor finds three solutions.
Not if you enter 14+742/1000 instead of 14*742/1000 ![]()
OK it will still find three solutions but only one of them would be real.
The equation obviously is chosen on purpose so that if it ends with 14 it only has one real solution and this fact will not change if you add xxx/1000.
BTW, the equation in the sheet you posted as first reply seems to be in some crazy manner corrupted! Even if you repair the multiply by 14 error it will yield wrong results. Not sure how you managed to get this messed up that way. The equations looks pefectly OK but it acts as if you had typed an invisible pair of parentheses.

How did you do that?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Mike Armstrong wrote:
The symbolic processor finds three solutions.
Not if you enter 14+742/1000 instead of 14*742/1000
OK it will still find three solutions but only one of them would be real.
I wasn't too sure on the correct format so I included both. ![]()
Werner Exinger wrote:
BTW, the equation in the sheet you posted as first reply seems to be in some crazy manner corrupted! Even if you repair the multiply by 14 error it will yield wrong results. Not sure how you managed to get this messed up that way. The equations looks pefectly OK but it acts as if you had typed an invisible pair of parentheses.
How did you do that?
I have no idea. I have just deleted the x and re-typed it and got the following.
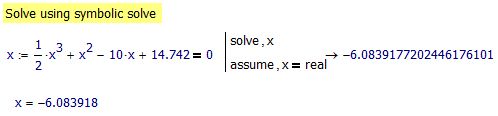
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here you are:
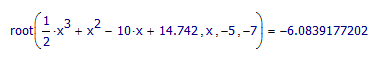
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How would I go about solving this equation manually First of all?
I guess thats a case for digging your head deep into your books, your lecture notes or whatever you have and maybe even look it up in the net.