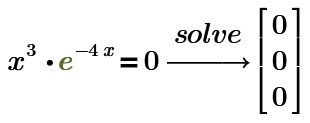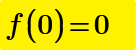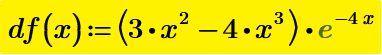Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
No solution was found
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No solution was found
Hi, im totally newbie.
I have 2 problems and i dont know hot to solve it 😕
Any ideas ?
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
The inequality:
This means: x<0 OR 0<x<3/4
Success!
Luc
What you show is the result of MC11 with Maple as symbolic engine. Unfortunately the symbolic engine was changed twice since then and the newest one (Axiom/FriCAS; the only one available in Prime 7) is not able to solve that inequality.
Here is a comparison done in Prime 6 showing of the results we get using the legacy symbolic (muPad) and the new one (Axiom/FriCAS). Interesting in both cases is the effects we get, when we simply use "solve" compared to those if we explicitly specify the variable x. There is also a big difference in the results depending on whether we are storing the derivative into a function or using it directly. Also note the effect "simplify" has on the result with the new symbolic.
Legacy Symbolic (muPad):
New symbolic (Axiom/FriCAS):
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
is this the only one solution? you can't solve the inequality with the "solve" method?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm constrained to Prime Express, since I don't have a license. (Express is free!) Symbolic operations (like solve) are "premium" features that Express will display but not execute, so I can see what you've done (as long as I don't resave your sheet) but I can't run it.
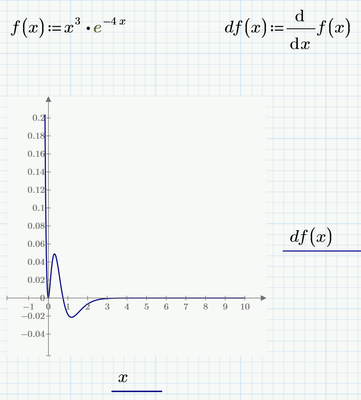
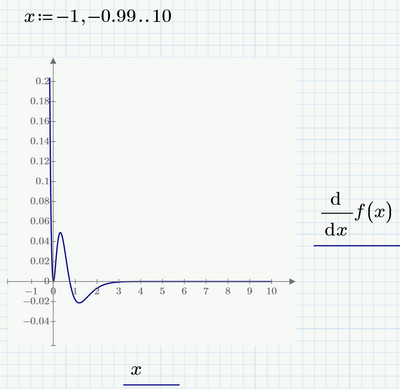
That said, symbolic operations never were a really strong feature in Mathcad and they have not improved in Prime. The numeric solution shows that the derivative function goes strongly positive for negative x, change the range of xx to see this. The derivative function goes to zero at x = 0, but it does not go negative until x = 3/4. So the root function (which Express will do) cannot find the root at zero, but it will find the root at 3/4. I suspect that the solve found a double root at zero because of two imaginary roots.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Page 2 Triple root is 0 and the f(0) = 0 with evaluate "=".
Page 4 df(x) must above the plot.
- Tags:
- Prime_7.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The inequality:
This means: x<0 OR 0<x<3/4
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
The inequality:
This means: x<0 OR 0<x<3/4
Success!
Luc
What you show is the result of MC11 with Maple as symbolic engine. Unfortunately the symbolic engine was changed twice since then and the newest one (Axiom/FriCAS; the only one available in Prime 7) is not able to solve that inequality.
Here is a comparison done in Prime 6 showing of the results we get using the legacy symbolic (muPad) and the new one (Axiom/FriCAS). Interesting in both cases is the effects we get, when we simply use "solve" compared to those if we explicitly specify the variable x. There is also a big difference in the results depending on whether we are storing the derivative into a function or using it directly. Also note the effect "simplify" has on the result with the new symbolic.
Legacy Symbolic (muPad):
New symbolic (Axiom/FriCAS):
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As described above, the new and only symbolic available in P7 is unable to solve this inequality.
According to plotting:
It works OK, if you either
- define a function for the derivative
- or if you define a range variable
I manually changed the lower limit on the abscissa to -1 in the first plot (quickplot) and in both cases the upper limit on the ordinate to 0.2.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator