Hi,
I am trying to solve the eigenvectors of matrix k-lambda*m, similar to [vec, val] = eig(k,m) in matllab.
However, there is no such built in function in Mathcad. I write a similar equation in solve block,
but mathcad tends to return to the trivial solution.
Is there a way to restrain mathcad from producing trivial solutions?
Thank you guys!
Best
Shawn
ACCEPTED SOLUTION
Accepted Solutions
Why don't you use the built-in functions genvals and genvecs ?
Zero tolerance is set to 12, otherwise we won't get those perfect zeros.
I guess one problem in your attempt is, that you are taking the square root when you define w´ while you should rather simply write w´:=polyroots(v) to get the generic eigenvalues.
But even then your solve block just provides the trivial solution as eigenvectors are not unique.
You could add some constraints like "the first component of each vector should be 1"
or "every vector should be of length 1"
or even
You may play around with smaller values of CTOL to get more accurate results. In Mathcad 15 I had no luck with values below 10^-5.
Regards
Werner
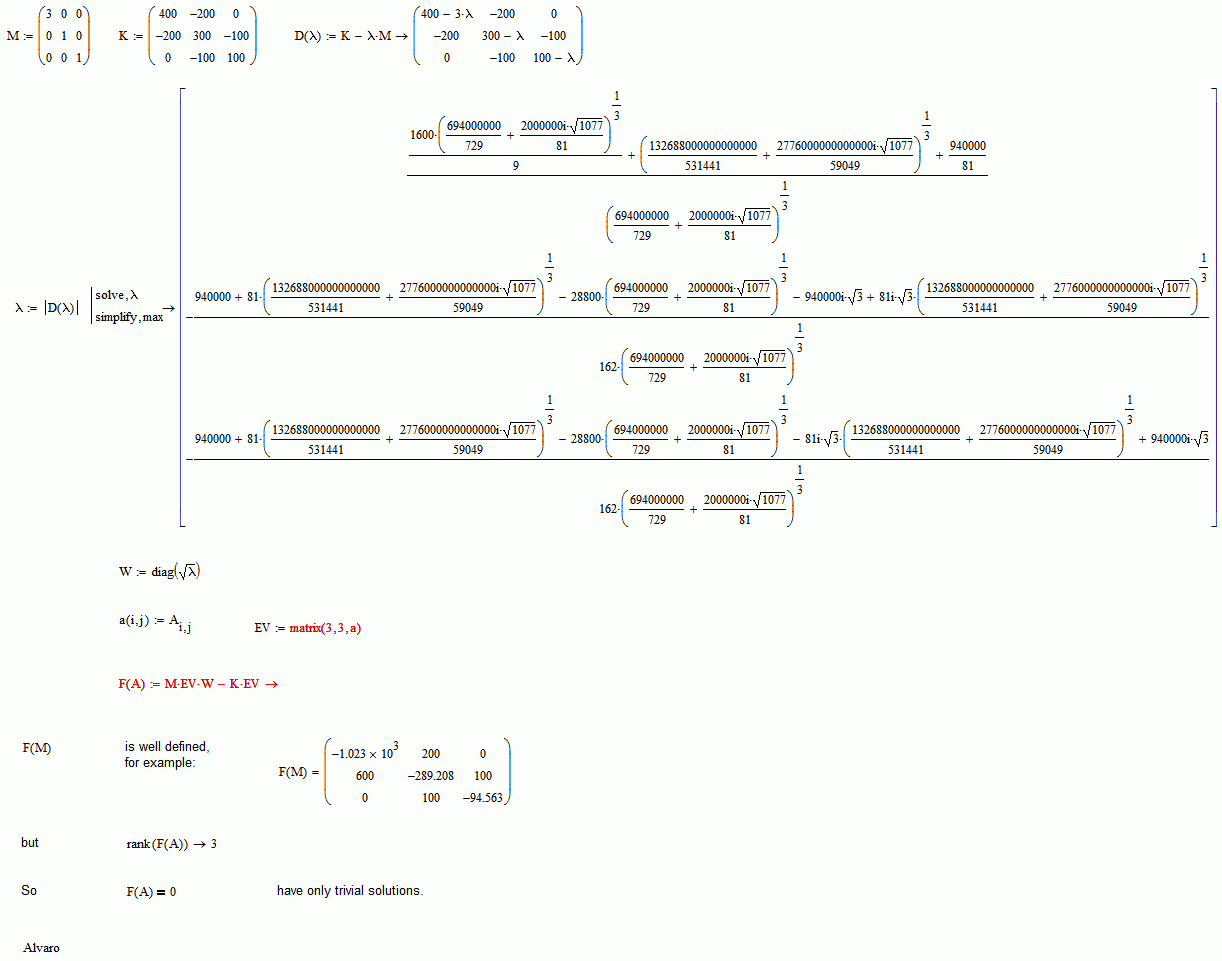
Hi Shawn.
No way. If MuPad don't make some mistakes, which could be, your system have rank 3, this is, all columns are independent, so, the system only have trivial solutions.
Best regards.
Alvaro.
Why don't you use the built-in functions genvals and genvecs ?
Zero tolerance is set to 12, otherwise we won't get those perfect zeros.
I guess one problem in your attempt is, that you are taking the square root when you define w´ while you should rather simply write w´:=polyroots(v) to get the generic eigenvalues.
But even then your solve block just provides the trivial solution as eigenvectors are not unique.
You could add some constraints like "the first component of each vector should be 1"
or "every vector should be of length 1"
or even
You may play around with smaller values of CTOL to get more accurate results. In Mathcad 15 I had no luck with values below 10^-5.
Regards
Werner
