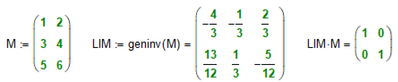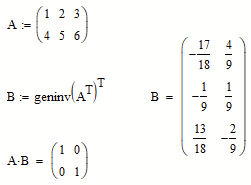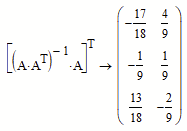Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Non-square matrix with left and right inverse matrices
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Non-square matrix with left and right inverse matrices
A non-square matrix can have left and right inverse matrices.
Left and right inverse matrices may not be the only ones. If a matrix has both left and right inverse, then it is invertible and m = n.
Let M be an m x n matrix, i.e. defining a linear mapping from Rn to Rm.
1. If n < m, then there can exist a left inverse L matrix n x m from Rm to Rn such that LA = E (the identity matrix), the condition of this: Ker A = 0 (the mapping A is one-to-one).
2. If n > m, then there can exist a right inverse R n x m matrix from Rm to Rn such that AR = E, the condition of this: Im A = Rn (mapping of A to the whole space).
How can we calculate RIM?
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
A non-square matrix can have left and right inverse matrices.
Left and right inverse matrices may not be the only ones. If a matrix has both left and right inverse, then it is invertible and m = n.
Let M be an m x n matrix, i.e. defining a linear mapping from Rn to Rm.
2. If n > m, then there can exist a right inverse R n x m matrix from Rm to Rn such that AR = E, the condition of this: Im A = Rn (mapping of A to the whole space).How can we calculate RIM?
?
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
A non-square matrix can have left and right inverse matrices.
Left and right inverse matrices may not be the only ones. If a matrix has both left and right inverse, then it is invertible and m = n.
Let M be an m x n matrix, i.e. defining a linear mapping from Rn to Rm.
2. If n > m, then there can exist a right inverse R n x m matrix from Rm to Rn such that AR = E, the condition of this: Im A = Rn (mapping of A to the whole space).How can we calculate RIM?
?
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Personally I would prefer Stuarts way, but if you feel so, you may also use "geninv" to get the desired result:
The calculation which is done behind the scenes when using the above shown way with "geninv" is actually this:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator