Notation for trig operations

[dBoggs]

I have a concern about the notation Mathcad uses for simple trig functions. I've had this concern for years, but it has come to the forefront again with the use of Prime, which (thankfully!) tries harder to make the equations look typeset.

In published material, the sine of x is written sin x. The sine of the ratio x/y is written sin x/y. And so on. (Imagine that my solidus "\" would in most cases be replaced by a stacked form of the ratio).

In Mathcad, these must be entered as, and appear as, sin (x), sin (x/y) and so on.

The typesetting rule is that the horizontal bar in a stacked fraction serves as the grouping parenthesis, so that putting () around x/y is redundant. Mathcad methodology apparently does not allow this convention.

Things get more confusing when we start performing operations on the operand of the sin function. For example, in typeset math the sine of the square of x is written sin x^2. The square of the sine of x would be written (sin x)^2, or possibly sin^2 x.

In Mathcad, I would therefore expect that when I see sin (x)^2 this means sin x^2, but it does not: Mathcad calculates (sin x)^2. If I WANT the sine of (x squared) in Mathcad, I have to write sin ((x)^2), which is quite awkward, and certainly not what you would see in a typeset book. If I wanted to calculate the sine of the square of the ratio x/y, I would have to enter sin ((x/y)^2). It should be sufficient to enter sin (x/y)^2 according to standard math typesetting rules, but doing this in Mathcad gives you the wrong answer.

I suspect that Mathcad's non-standard handling of this has caused more than a few errors over the years.

Comments?

[MikeArmstrong]

In Mathcad, I would therefore expect that when I see sin (x)^2 this means sin x^2, but it does not: Mathcad calculates (sin x)^2. If I WANT the sine of (x squared) in Mathcad, I have to write sin ((x)^2), which is quite awkward, and certainly not what you would see in a typeset book. If I wanted to calculate the sine of the square of the ratio x/y, I would have to enter sin ((x/y)^2).

Can't you just write.

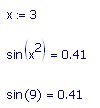
Mike

Message was edited by: Mike Armstrong

[RichardJ]

Comments?

Use the prefix operator.

This is not yet supported in Prime.

[dBoggs]

The problem is that, if I saw a calculation sheet that said sin (x)^2 out of context, I would assume that this meant the sin of the square of x. But in the Mathcad context it doesn't work that way, it means the square of the sin of x.

Richard's prefix operator makes it look right. (This is new to me, I don't quite understand it, and may not try to if it is not supported in Prime.)

Thanks for the comments. I still think its an "undesirable characteristic" in Prime, or earlier for that matter since most will not take the trouble to use the prefix operator. It IS a little obscure, and I think that especially in Prime the equations should conform to standards by default without resorting to tricks.

[RichardJ]

It IS a little obscure

I disagree.

It's very obscure

The problem is that, if I saw a calculation sheet that said sin (x)^2 out of context, I would assume that this meant the sin of the square of x. But in the Mathcad context it doesn't work that way, it means the square of the sin of x.

But the notation is consistent with the notation for other functions. If you make the standard notation for the trig functions different to that for all other functions then the "other half" will complain about confusion.

[MikeArmstrong]

What about the method I proposed?

Mike

[RichardJ]

The problem is that, if I saw a calculation sheet that said sin (x)^2 out of context, I would assume that this meant the sin of the square of x.

I must admit, I wouldn't. Becuase it doesn't say sin (x)^2, it says sin(x)^2, and that space (or lack of it) makes all the difference.

[MikeArmstrong]

Good shout. Totally forgot about them.

Mike

[ValeryOchkov]

In 2002 I knew how to do it! But now...

See my old tip for Mathcad users!

I must search the Mathcad file!

(sin x - no problem by help the prefix operator)

[MikeArmstrong]

I really don't see the issue here.

I provided an example without the need to use the prefix operator.

Mike

[RichardJ]

I really don't see the issue here.

I provided an example without the need to use the prefix operator.

For sin(x^2), but not for the others, such as sin^2 x. Some can only be done with the prefix operator.

[MikeArmstrong]

For sin(x^2), but not for the others, such as sin^2 x. Some can only be done with the prefix operator.

Missed that.

Using Mathcad for so long sin(x)^2 actually looks correct to me.

Mike

[dBoggs]

Thanks everybody for the lively discussion.

I will try to restate the issue as clearly as possible, using the example: sine of 1/2 and 1/4 (radians, of course).

1. sin 1/2 = .479 in both std math (SM) and Mathcad (MC).

2. sin 1/4 = .247 in both SM and MC

3. sin (1/2) = .479 in both SM and MC

4. sin (1/2)^2 = .247 in SM (as I would expect)

= .230 in MC (not expected)

5. sin^2 (1/2) = .230 in SM (as I would expect)

... cannot be done in MC

6. (sin (1/2))^2 = .230 in SM and MC

When Mathcad wants to represent the square of the sine of something, I think it should use form 6 not form 4.

In my mind the same thing applies to certain other common functions, such as log(*).

As far as other functions go, this indeed may be the biggest argument against making the change, as pointed out by Richard. Nevertheless, when one sees in math notation

(stuff of any kind)^n

it is only logical to assume that the n exponent *always* operates on whatever was enclosed by the preceeding matched parenthesis. Mathcad formatting does not honor that rule when the (*) is the argument of a function.

Tricks that can be used to make Mathcad look correct is an interesting topic but not germain to the issue, because most people will never use them, and if they do it might confuse a Mathcad-savy reader. The real issue is what person B might assume when he sees a page of calcs produced by person A. B might not even know that A used Mathcad! In this case I think B is likely to interpret it wrong (i.e. wrong according to Mathcad).

[MikeArmstrong]

5. sin^2 (1/2) = .230 in SM (as I would expect)

... cannot be done in MC

It can be done, but not exactly as you wanted.

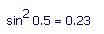
But the real notation should be.

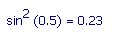
Now that reads to me sin0.5 x sin0.5.

4. sin (1/2)^2 = .247 in SM (as I would expect)

= .230 in MC (not expected)

Can be displayed like this.

Tricks that can be used to make Mathcad look correct is an interesting topic but not germain to the issue, because most people will never use them, and if they do it might confuse a Mathcad-savy reader. The real issue is what person B might assume when he sees a page of calcs produced by person A. B might not even know that A used Mathcad! In this case I think B is likely to interpret it wrong (i.e. wrong according to Mathcad).

The thing is person B needs to be competent enough to check persons A work, otherwise it won't make a difference how it is laid out.

Mike

[RichardJ]

4. sin (1/2)^2 = .247 in SM (as I would expect)

= .230 in MC (not expected)

There is no such notation in Mathcad. The notation is sin(1/2)^2. There is a big difference, because the space you keep adding, but that does not exist in Mathcad, significantly changes what is implied by the expression.

5. sin^2 (1/2) = .230 in SM (as I would expect)

... cannot be done in MC

Yes it can. I just showed you how to do it

6. (sin (1/2))^2 = .230 in SM and MC

When Mathcad wants to represent the square of the sine of something, I think it should use form 6 not form 4.

You can write form 6 if you want.

[StuartBruff]

DARYL BOGGS wrote:

I have a concern about the notation Mathcad uses for simple trig functions. I've had this concern for years, but it has come to the forefront again with the use of Prime, which (thankfully!) tries harder to make the equations look typeset.

In published material, the sine of x is written sin x. The sine of the ratio x/y is written sin x/y. And so on. (Imagine that my solidus "\" would in most cases be replaced by a stacked form of the ratio).

In Mathcad, these must be entered as, and appear as, sin (x), sin (x/y) and so on.

The typesetting rule is that the horizontal bar in a stacked fraction serves as the grouping parenthesis, so that putting () around x/y is redundant. Mathcad methodology apparently does not allow this convention.

Things get more confusing when we start performing operations on the operand of the sin function. For example, in typeset math the sine of the square of x is written sin x^2. The square of the sine of x would be written (sin x)^2, or possibly sin^2 x.

In Mathcad, I would therefore expect that when I see sin (x)^2 this means sin x^2, but it does not: Mathcad calculates (sin x)^2. If I WANT the sine of (x squared) in Mathcad, I have to write sin ((x)^2), which is quite awkward, and certainly not what you would see in a typeset book. If I wanted to calculate the sine of the square of the ratio x/y, I would have to enter sin ((x/y)^2). It should be sufficient to enter sin (x/y)^2 according to standard math typesetting rules, but doing this in Mathcad gives you the wrong answer.

I suspect that Mathcad's non-standard handling of this has caused more than a few errors over the years.

Comments?

Judging from the ISO 31-11, I'm not sure you are right in your interpretation of how such expressions should be typeset.

Section 11-7.1 : f represents function f and may also be written as x↦f(x)

Section 11-7.2 : f(x) represents the value of function f at x

Section 11-7.7 : Example is 1/(sin(x-a))

Section 11-9.2 : sin x represents the sine of x, however ...

Section 11-9.2 : example is (sin x)ⁿ, etc are often written sinⁿx

However, the settling points for me are in Section 0.2, where the 4th and 5th paragraphs state:

The argument of a function is written in parentheses after the symbol for the function, without a space between the symbol for the function and the first parenthesis, eg f(x), cos(ωt+φ). If the symbol for the function consists of two or more letters and the argument contains no operation sign, such as +;-;x;-; or /, the parentheses around the argument may be omitted. In these cases, there should be a thin space between the symbol for the function and the argument, eg ent 2,4; sin nx; archosh 2A, Ei x.

If there is any risk of confusion, parentheses should always be inserted. For example, write cos(x)+y or (cos x)+y; do not write cos x+y, which could be mistaken for cos(x+y).

Consequently, I believe that sin x/y should always be written sin(x/y).

Stuart

Message was edited by: Stuart_Bruff to correct minor typos.

[dBoggs]

Stuart,

Thanks for the comments and the ISO reference. I always assumed there must me a set of standards for this sort of thing but didn't know where to go.

Unfortunately, I don't have the ISO standard (of course!) and a Google search only leads me to places where ISO 31-11 appears only to be definitions of "mathematical signs and symbols" and doesn't include your examples. There must be a lot more that I just can't find.

Regarding the 4th paragraph that you reference, I can't disagree with anything there, but I also don't see its relevance to the issue at hand.

Regarding the 5th paragraph, I agree completely. But, if the ratio x/y is stacked instead of in-line, then:

1. There is no possibility of confusion

2. Every quality publisher of technical (and I do mean EVERY) that I know of utilizes the stacked form, without parenthesis, as being unambiguous. It is so common, in fact, that I have pulled a dozen or more math, science, and engineering books from the hundred or so in my library, and haven't found a single exception. So if the is a *rule* against this (and I don't think your examples show one), the overwhelming *practice* is to avoid the redundancy of the enclosing ( ). Try this experiment yourself and let me know the results.

But more to my original point, the notation sin(x)^n IS confusing (at best) and ambiguous (at worst). It should be written either (sin(x))^n or sin(x^n), depending on the meaning intended. This is the problem I have with Mathcad.

I think one could easily argue (and the publishers do this routinely) that the first case could be written (sin x)^n, since there is no confusion or ambiguity, and the second could also be written sin x^n for the same reason. I see this form often in my books. I would never even thought of interpreting it as (sin x)^n.

It's analogous to an expression like ab^x (try to imagine the x set as a superscript). Nobody reading typeset material would interpret this as (ab)^x. It is a standard (and I do mean *standard*) way of saying a(b^x). I defy anyone to find a recognized technical publisher that doesn't follow this convention.

Well, I know this discussion may be rambling on with no possibility of agreement, but it is a very interesting subject to me.

Daryl

[StuartBruff]

Regarding the 4th paragraph that you reference, I can't disagree with anything there, but I also don't see its relevance to the issue at hand.

The relevance lies in the statement about "no operation sign".

The argument of a function is written in parentheses after the symbol for the function, without a space between the symbol for the function and the first parenthesis, eg f(x), cos(ωt+φ). If the symbol for the function consists of two or more letters and the argument contains no operation sign, such as +;-;x;-; or /, the parentheses around the argument may be omitted.

Even a stacked divide is an operator sign and should therefore necessitate the use of parentheses.

Regarding the 5th paragraph, I agree completely. But, if the ratio x/y is stacked instead of in-line, then:

1. There is no possibility of confusion

2. Every quality publisher of technical (and I do mean EVERY) that I know of utilizes the stacked form, without parenthesis, as being unambiguous. It is so common, in fact, that I have pulled a dozen or more math, science, and engineering books from the hundred or so in my library, and haven't found a single exception. So if the is a *rule* against this (and I don't think your examples show one), the overwhelming *practice* is to avoid the redundancy of the enclosing ( ). Try this experiment yourself and let me know the results.

But more to my original point, the notation sin(x)^n IS confusing (at best) and ambiguous (at worst). It should be written either (sin(x))^n or sin(x^n), depending on the meaning intended. This is the problem I have with Mathcad.

I think one could easily argue (and the publishers do this routinely) that the first case could be written (sin x)^n, since there is no confusion or ambiguity, and the second could also be written sin x^n for the same reason. I see this form often in my books. I would never even thought of interpreting it as (sin x)^n.

They are sinners, all of them, and should be burnt at the stake! (provided such stake conforms to the appropriate standard ... I do miss the Middle Ages, we could have had some really interesting standards "Ye shall cut the throat of thy prisoner from behind using a left to right stroke. This bringeth quick relief to the prisoner and, more importantly, minimizes blood splatter on ye doublet. Avoid ye rusty knife that does not conform to King's Standard 00-007 as prisoners having their throats cut by a blunt implement, tend to scream at such volume that the KS 00-25 Vol 2, Human Factors - Massacring, Section 3.4 is breached and thy Health and Safety Sarjeant shall haveth kittens.")

Anyway, as pointed out elsewhere, Mathcad does allow you to display '(sin x)ⁿ' using the prefix operator. Now what would be useful is the ability to right-click on a definition and select the operator display form.

It's analogous to an expression like ab^x (try to imagine the x set as a superscript). Nobody reading typeset material would interpret this as (ab)^x. It is a standard (and I do mean *standard*) way of saying a(b^x). I defy anyone to find a recognized technical publisher that doesn't follow this convention.

There are established precedence rules for exponents.

Stuart

[RichardJ]

It's analogous to an expression like ab^x (try to imagine the x set as a superscript). Nobody reading typeset material would interpret this as (ab)^x. It is a standard (and I do mean *standard*) way of saying a(b^x). I defy anyone to find a recognized technical publisher that doesn't follow this convention.

Convention for what? Convention for mathematical typesetting, yes, but not for typesetting programming expressions. The reason ab^x is unambiguous in mathematical typesetting is because variable names with more than one character are not allowed. Unless you are proposing that Mathcad ban all variable names of more than one character then ab^x means the variable ab raised to the power x, and it could not mean anything else. Multiplication must be shown as something, even if only a thin space. Also, even in a mathematical expression a(b^x) could be interpreted as the function a taking the argument b^x. You could only figure out what was actually meant from the context or the accompanying text. If you want unambiguous multiplication you need a space (a thin space perhaps, but a space): a (b^x).