Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Numerical Precision in MathCAD
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Numerical Precision in MathCAD
Numerical Precision in MathCAD: which is MathCAD numerical precision? what is the maximum number of significant decimal digit ? To which minimum values TOL, CTOL could be set?
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why the symbolic processor ( by using float ) could operate effectively well beyond 15 digits?
The short answer is that it does the calculations in a different way. For the long answer, see here: Arbitrary-precision arithmetic - Wikipedia, the free encyclopedia
in which cases it could replace the numerical evaluation?
In any case where the symbolic processor understands the expression you are trying to evaluate. However, there is no way to use the higher precision of the result of that evaluation in a subsequent calculation, because if you store it in a variable you are limited to the 64 bit representation of the number.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Massimiliano Nori wrote:
Numerical Precision in MathCAD: which is MathCAD numerical precision? what is the maximum number of significant decimal digit ? To which minimum values TOL, CTOL could be set?
Mathcad uses (near enough) standard IEEE 64-bit format floating point arithmetic, meaning you get about 15 decimal digits (53 bit mantissa) for user-level values. Internally, it uses IEEE 80-bit floating point for a bit more precision (about 17 decimal digits), presumably to make sure that the 15-digit "user" precision isn't too badly affected by round-off in the least significant digits.
The TOL and CTOL affects will depend upon the nature of the problem being solved and the solver characteristics.
The symbolic processor uses arbritray length arithmetic and operates effectively well beyond a mere 15 decimal digits.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you Stuart,
some further requests of clarifications:
In Result Format: Number format / decimal places could be set up to 17 , these correspond to the significant 17 decimal places according IEE 80-bit?.
Furthermore in Tolerance/ zero threshold and complex threshold could be set up to 307. What this limit represent?
In case of a non-linear parameters regression with Minerr ( LM ) and Minimize respectively , How ( and if ) CTOL and TOL affect the calculations. Which are TOL and CTOL minimum absolute value ?
Symbolic processor is activated by Symbolic Keyword Toolbar functions and symbolics Tab . Arbitrary length arithmetic to which maximum number of significant digit correspond ?
Massimiliano
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Massimiliano Nori wrote:
some further requests of clarifications:
In Result Format: Number format / decimal places could be set up to 17 , these correspond to the significant 17 decimal places according IEE 80-bit?.
Yes. The extra digits are only really of any use when you are displaying the result of a expression evaluation, not for displaying the value of a variable (which is stored as a 64-bit float)
Furthermore in Tolerance/ zero threshold and complex threshold could be set up to 307. What this limit represent?
This is the applicalbe exponent (power of 10) range. For example, by default Mathcad hides number <= 10^-15 by displaying them as 0, similarly imaginary components <= 10^-10. Eg,

In case of a non-linear parameters regression with Minerr ( LM ) and Minimize respectively , How ( and if ) CTOL and TOL affect the calculations. Which are TOL and CTOL minimum absolute value ?
Not sure off the top of my head, but I think they look at the difference between the desired result and the calculated result at any stange and if they are within the tolerance then they determine that it's close enough.
Symbolic processor is activated by Symbolic Keyword Toolbar functions and symbolics Tab . Arbitrary length arithmetic to which maximum number of significant digit correspond ?
I haven't tested the practical internal limits (there's a 250 digit display limitation), but it's several hundred digits at least ...
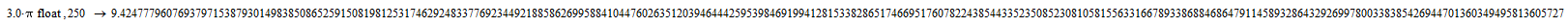
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why the symbolic processor ( by using float ) could operate effectively well beyond 15 digits? and in which cases it could replace the numerical evaluation?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why the symbolic processor ( by using float ) could operate effectively well beyond 15 digits?
The short answer is that it does the calculations in a different way. For the long answer, see here: Arbitrary-precision arithmetic - Wikipedia, the free encyclopedia
in which cases it could replace the numerical evaluation?
In any case where the symbolic processor understands the expression you are trying to evaluate. However, there is no way to use the higher precision of the result of that evaluation in a subsequent calculation, because if you store it in a variable you are limited to the 64 bit representation of the number.





