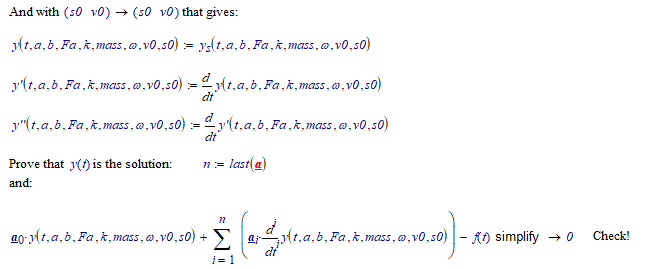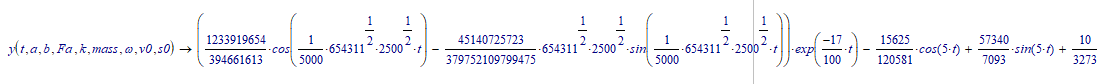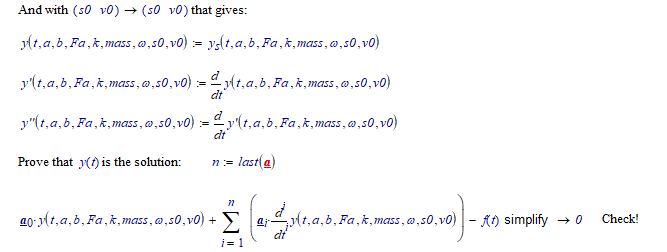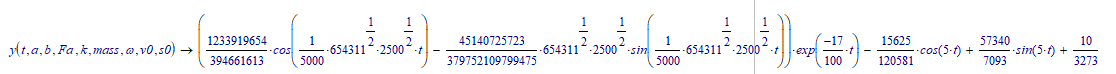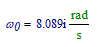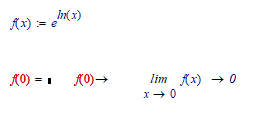Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
ODE Solver - errors with differential equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ODE Solver - errors with differential equation
Hey,
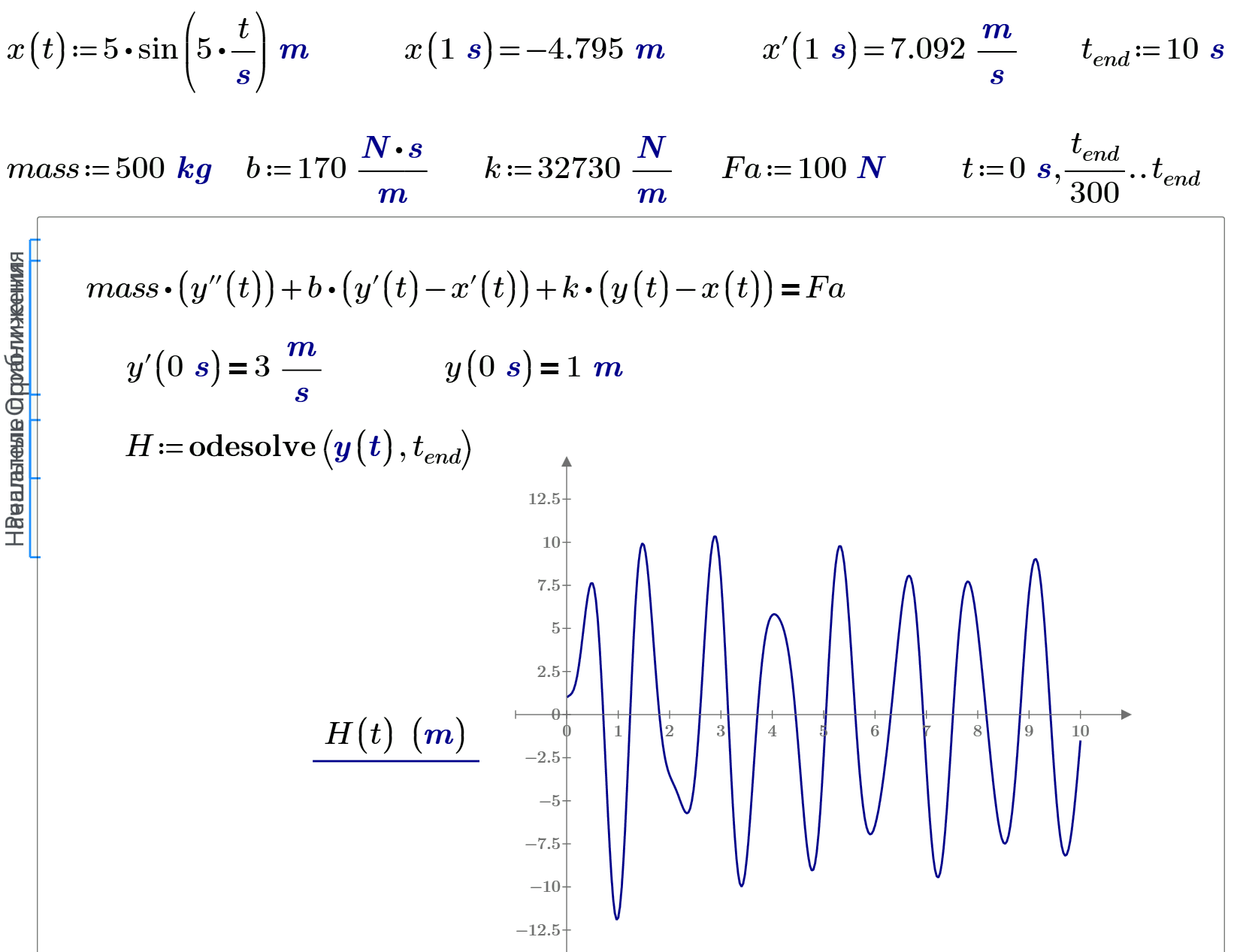
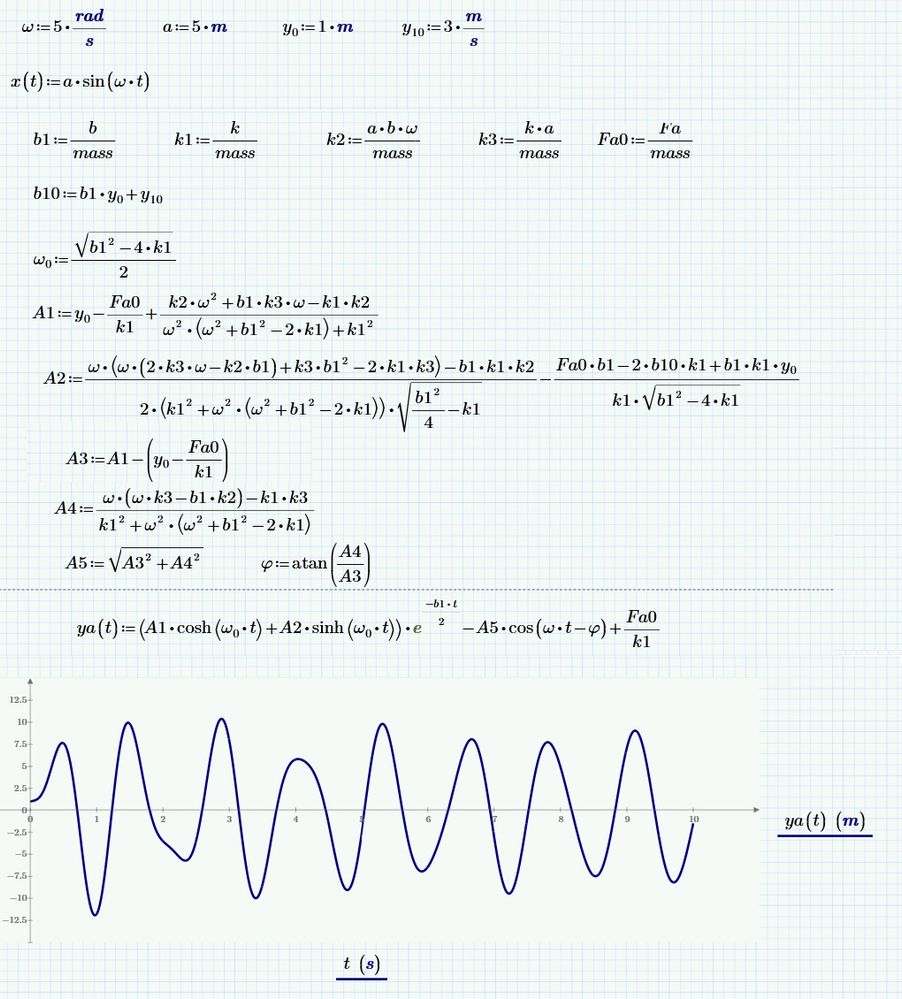
I am trying to model the second order differential equations for the shock absorber. I would like to get the funtion of the movement of the mass. I am getting errors from the Solve Block in MathCAD, and I cannot understand where is it coming from. I suppose the reason is the sin function x(t), but I have no idea how can I write it differently. Without units the solver was working fine, but with units I get always an error. I am uploading the MathCAD file.
I would be glad for some hints and tipps! Any help is welcome! ![]()
Best regards,
Jolanta
- Labels:
-
Calculus_Derivatives
-
Mathcad Usage
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ValeryOchkov, thank you for your answer ![]() It is veeery helpful, I was stuck with it for many hours...
It is veeery helpful, I was stuck with it for many hours...
But can you elaborate it a little bit, for example why should I write it like this:
I do not get this t over s 🙂
Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry! I cannot see your picture.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm, so I upload the snapshot with this equation I don't understand, I don't know why it is not visible in previous message 😞 cheers!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you (want to) work with units, you need to - consistently - work with units.
The argument to the sin function (or any other trig function or log, ln, and exp) can NOT have units.
Either divide the t by its unit (s), or give the 5 a unit ( something with Hz...).
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
If you (want to) work with units, you need to - consistently - work with units.
The argument to the sin function (or any other trig function or log, ln, and exp) can NOT have units.
Either divide the t by its unit (s), or give the 5 a unit ( something with Hz...).
Success!
Luc
Man has 7 (nice number) senses: sight, hearing, smell, touch, taste, sense of balance and a sense of ... units!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
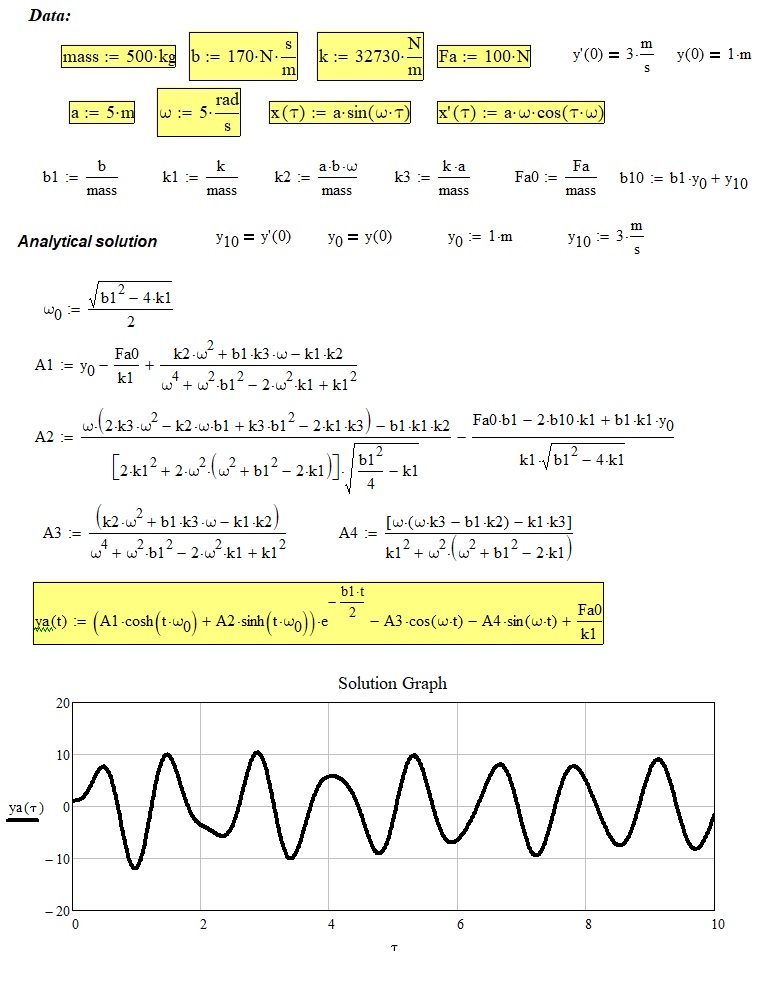
You can't do this exactly in Prime. But with a little handwork, and using the laplace transform, you should be able to work this out...
(Note that the expression for ys() stretches much further to the right...)
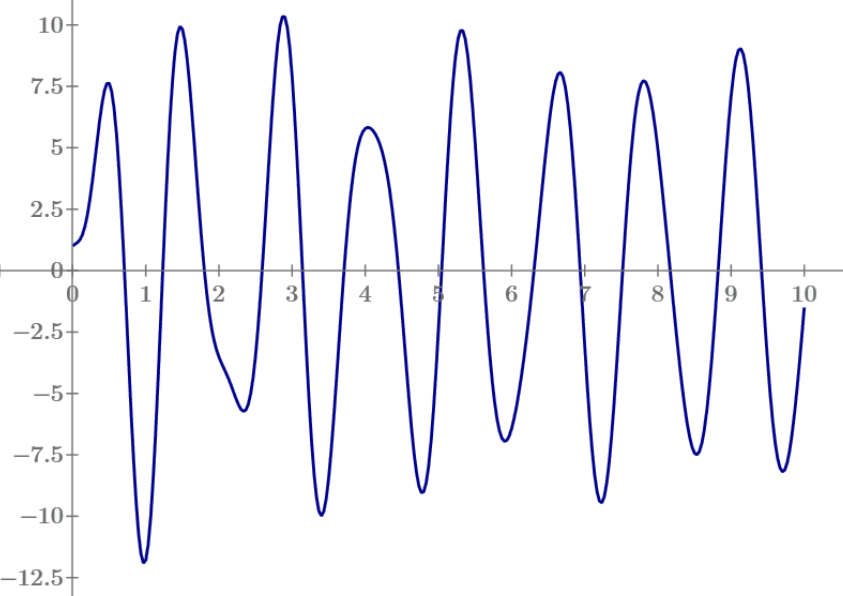
Note that we get the exact solution here (not a numerically approximated one).
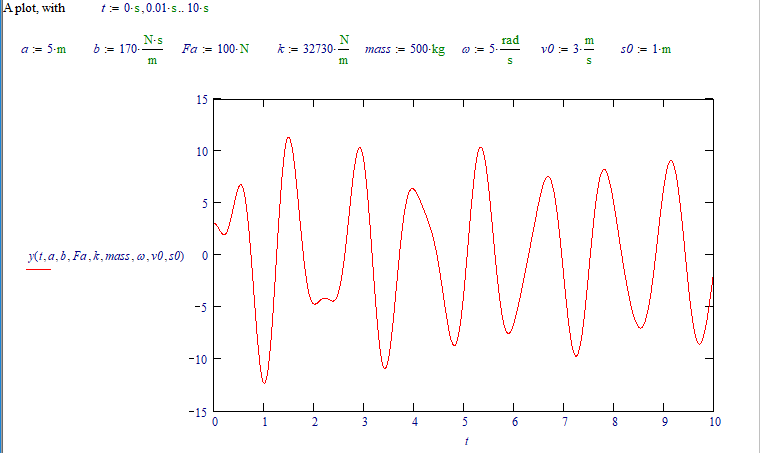
I wonder if, when you take smaller time steps in the odesolve, the bump at about 2 seconds shows there as well.
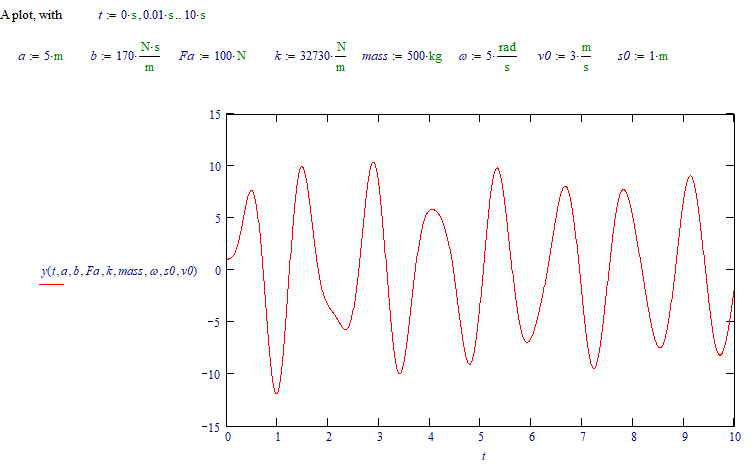
And with those values, for a, b...v0 (all SI units) the function ys() is:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
У нас такую кривую называют... бык на ходу пописал на дорогу!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Correction.
I messed up a few variables and got an incorrect result (that didn't match the Odesolve graph.).
Here's a corrected symbolic solution:
(now the bump at about 2 seconds is gone)
The full solution (for the given values of constants) is:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi JolantaPers,
es ist so einfach....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One other way to do in the top of Mathcad 15 sheet
m:=1 s:=1 kg:=1 N:=1 etc
But it is not good too. Better use Prime!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I was wondering why you get a sinh and cosh ( as multiplicands of e^...), where I get sin and cos (non-hyperbolic).
The reason is that you define
is you calculate this you get:
The sinh of a pure imaginary argument is a sin (multiplied with i) and the cosh of a pure imaginary argument is a cos.
That explains the difference between the two symbolic solutions.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
They are equivalent representations of the same function. How to say: instead of writing x I can also write exp (ln (x)) does not change anything, the result is always the same. Further, but not the last, simplification:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
" instead of writing x I can also write exp (ln (x)) does not change anything, the result is always the same"...
Careful: that may be true for all x except a few...or at least one.
Only in the limit does x=exp(ln(x) for x->0.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Luc ............. you're really a great luminary.