Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Obtaining eigenvalues of an eigenfunction
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Obtaining eigenvalues of an eigenfunction
Hi, i'm studying Green Functions.
I need to obtain the positive eigenvalues of a function, at this time just for first six values, m=1..6
Can i do this in mathcad Prime 3.1??
there's a attached file.
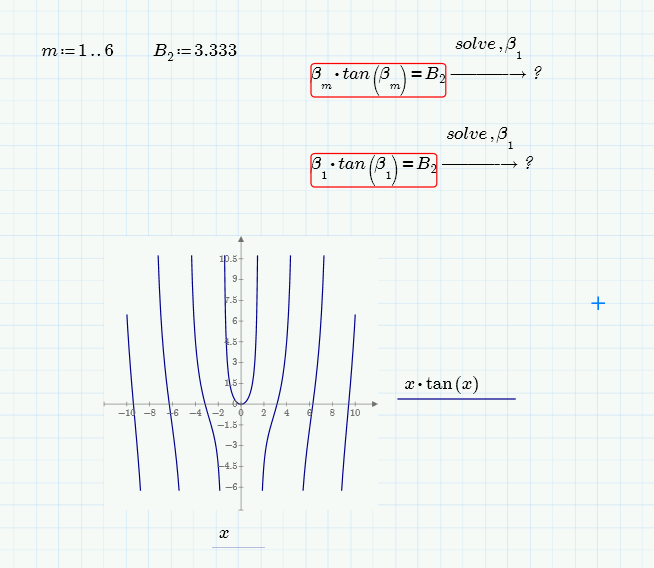
Thanks in advance.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The symbolic solve is not helpful in this case. Better use a numeric solve block or the root-function.
Maybe the attached file helps.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The symbolic solve is not helpful in this case. Better use a numeric solve block or the root-function.
Maybe the attached file helps.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
thank you very much!
I still have a question. I modified your file, and it still appear its correct to me. I modified just to get de positive values of beta, starting the first positive value in beta_1.
Is this version still right?
thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, unfortunatly I can't read P3.1 files, just P3.0 ones. PTC had decides that even subversions should not backward compatible.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
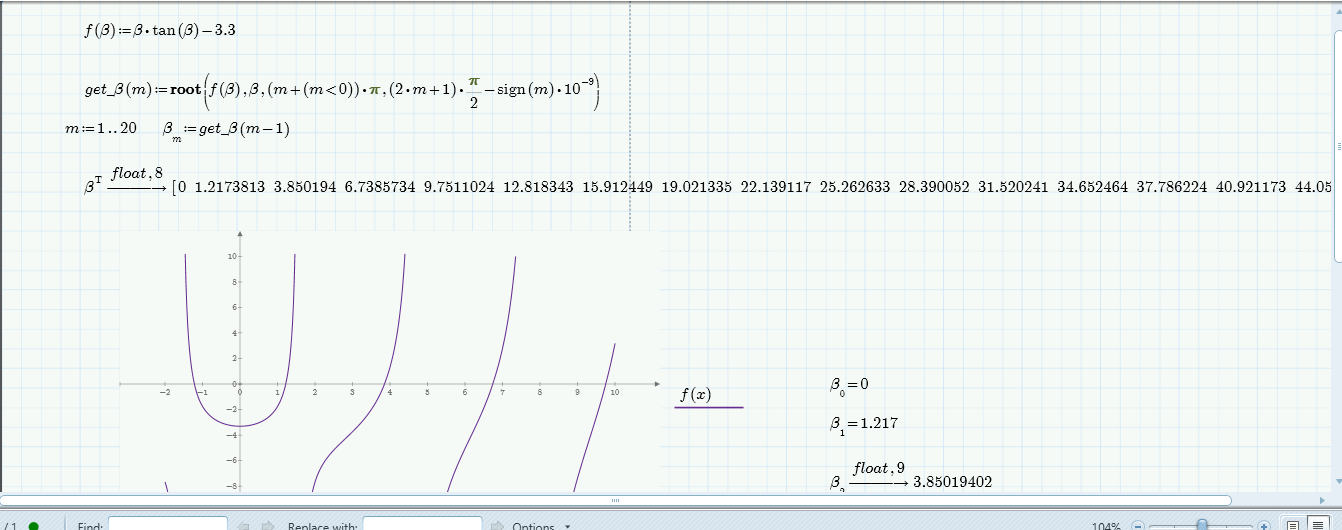
I see. Obviously the results ar correct with the exception of the first vector entry - zero is not a solution!
You get this value because Prime by default numbers vector elements beginning with zero. The first value you assign is the one with index 1 (range m), so element with index 0 defaults to zero.
better assign beta[m-1:=get_beta(m-1) or use a range m:=0..19 and beta[m:=get_beta(m).
I have used a rather sophisticated expression in the root command. The last two arguments have to be one value to the left and one value to the right of the root. For positive values the last argument has to be a value slightly to the left of an uneven multiple of pi/2 (pole), but for negative values we need a value slightly to the right of a negative pole. Thats the reason for the sign-function and the i<0 expression (which yields either 1 or 0). Guess the expressions could be simplified if only positive values are needed.
You could also use root with a different flavor without those two arguments but then you would have to provide a guess value and its hard to control which one of the solutions to get using a guess value. The same applies to using a solve block - again you would need a guess.
Here is a way to use a solve block function and still we have control which value to get. The way its written this function won't find the first negative solution but as you seem to look for positive values I haven't looked for a solution.

WE





