Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
One catenary problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One catenary problem
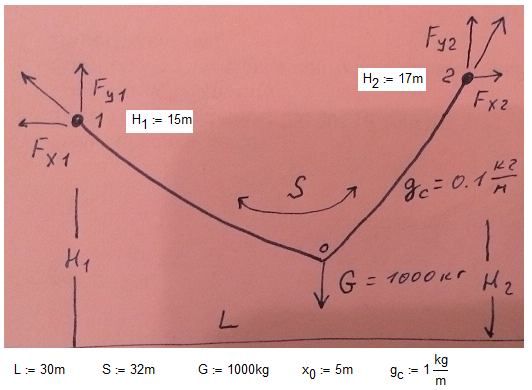
The description of the problem is here - http://communities.ptc.com/videos/1549#comment-11596
Help me please! My first step is in attach. Is it any right direction?
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Many good people in the past were victims of what they believed to be common sense
But in 99.9..% cases common sense = science!
I'd be happy to be able to believe the solutions will be catenaries, so maybe you can explain how a linear function can be a special case of a catenary,
Sorry, no a linear function a+b x, but I tell about a catenery like, near straight line!
I think this massage #100 is a dead point of this discussion. I would like to begin new one in new branch of this forum Or on one other Math forum. On one forum, where man does not say "I feel it is not correct, bu I do not know why!"

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery, the catenary came up here in the forum quite some many times and I guess you were involved in most if not all of those discussions 😉
Jan sent a very pretty video made with Blender (Mathcad animation can't cope with that) here: http://communities.ptc.com/message/198322#198322
Maybe Richards fine solution to a much more sphisticated and complex problem may help you. Its in the same thread here: http://communities.ptc.com/message/199100#199100
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Valery, the catenary came up here in the forum quite some many times
Thanks, Werner, I know this solutions.
But I would like to use more simple Method - the block Given-Find for new solution.
And do not know is it possible!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You you already assume that the left and right part are catenaries.
Just a quick idea (without closer thinking about): Lets look at the left side. This catenary has its (imaginary) lowest point at x01. Somewhere between Point 1 and this lowes point is the weight G. Shouldn't the weight of the chain from the point of the weight G and its lowest point (x01, that is the weight of the chain that doesn't exist) be the same as G?
At first sight I stumbled over the assumption Fx1=-Fx2 but i seems to be OK, I guess.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, it is one good idea.
We must create n equations with n unknowns. But can Mathcad solve this non linear system of 9-12 equations?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But can Mathcad solve this non linear system of 9-12 equations?
We'll see as soon as we have all necessary equations 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
But can Mathcad solve this non linear system of 9-12 equations?
We'll see as soon as we have all necessary equations 😉
We not you ![]() I am glad to see it.
I am glad to see it.
Why?
I have wish but not zeit, pardon, time.
Help me please, Werner!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have wish but not zeit, pardon, time.
Same here 😉 Maybe later.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
11 unknowns, 9 equations and no solution found 😞
Maybe we should not expect two catenaries.
Look if the chain has to hold a bridge - at equidistant points we may apply vertical ropes to hold the weight- This time we don't get a catenary but a parabola!
So maybe its a good idea to set up the differential equation(s) and see what kind of solution we have-.
On the other side - if the weight is big in relation to the rope/chain weight we can neglect the chain weight completely and get just two straight lines
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Look if the chain has to hold a bridge - at equidistant points we may apply vertical ropes to hold the weight- This time we don't get a catenary but a parabola!
One picture on the wall in my Mathcad-study:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You need to draw the vertical lines so the chain gets the form of a parabola. Otherwise the chain has the form of a catenary and the road is down the river.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
You need to draw the vertical lines so the chain gets the form of a parabola. Otherwise the chain has the form of a catenary and the road is down the river.
We cannot see these lines - fog ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
11 unknowns, 9 equations and no solution found 😞
Stll one letter missing
Stll one letter missing ![]()
I understand this without one letter, but Mathcad does not understand our system without two equation ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As the error now is that it doesn't find a solution adding equations will not help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Werner Exinger wrote:
11 unknowns, 9 equations and no solution found 😞
Stll one letter missing
Hmm - not my text in the last line of the quote.
But Mathcad sure is able to solve underdetermined systems of equations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Valery Ochkov wrote:
Werner Exinger wrote:
11 unknowns, 9 equations and no solution found 😞
Stll one equation missing
Hmm - not my text in the last line of the quote.
It was your first variant of the answer - in an e-mail to me from PlanetPTC![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I often edit my posts after the first send off. Correcting typos or including further ideas as long nobdy had replied.
The missing was an error as I counted 10 unknowns instead of the eleven 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
I often edit my posts after the first send off. Correcting typos or including further ideas as long nobdy had replied.
Me too.
But we say in Russia - The word is not a sparrow - it will take off and we did not catch it!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
On the other side - if the weight is big in relation to the rope/chain weight we can neglect the chain weight completely and get just two straight lines
It is for guess values of the Given-Find block!
And it will be good to solve this task in Prime with m, kg, N etc in one vector.
But Prime has not animation.
I would like to have an animation of this task!
We can solve the task in Prime and than create an animation in M15!
But at first to solve! Let do it together!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
As already stated - I guess there are no catenaries at all but just straight lines (1000 kg on a 3 kg rope/chain - neglect the rope!).
All you will see if you animate is the weight moving along the path of an ellipse until it is at its lowest point. The two Points the chain is fixed to being the focal points of that ellipse. Gardener constructiion of an ellipse.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
We must find y0 and draw two catenary between (x1, h1) - (x0, y0) and (x0, y0) - (x2, h2).
Or?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not catenaries but just straight lines because the load is very big compared to the weight of the chain.
And I am not sure we get catenaries if we apply just a very small weight!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exing
Werner Exinger wrote:
Not catenaries but just straight lines because the load is very big compared to the weight of the chain.
Sorty, but the load can be small too.
We can create an animation with the load from 0 to N kgf.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorty, but the load can be small too.
We can create an animation with the load from 0 to N kgf.
So I guess you will have to start wth the differential equation(s) first.
We have one catenary for load=0 and we sure have two straight lines for load=infinity.
What do we have inbetween? I guess no catanaries!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Sorty, but the load can be small too.
We can create an animation with the load from 0 to N kgf.
So I guess you will have to start wth the differential equation(s) first.
We have one catenary for load=0 and we sure have two straight lines for load=infinity.
Sorry.
The straight line is a partial (limit) case of catenary.
Werner Exinger wrote:
What do we have inbetween? I guess no catanaries!
We have catanaries!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
We have catanaries!
Proof!?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mikko Hinkkanen wrote:
Read wikipedia http://en.wikipedia.org/wiki/Catenary
Wikipedia is most of the times useful but never will replace a proof!
But foremost: Please read not just the catchwords "chain" and "catenary" and trigger but look and read closely whats really discussed here! We have a chain wich is loaded at a single point by a weight (and later we would strive for an equilibrium of forces). The usual basic approach to set up the differential equation (which isn't that easy to solve after all) which leads to a catenary does not fit here.
Wikipedia cover some alterations from the basic setup (the usual uniformly distributed load which leads to a parabola and some others) which all do not lead to a catenary but rather would Wikipedia leave the reader with DEs which are not solved. At least I haven't seen single point load covered in that article.
So while I don't say that we have no catenaries in this problem (honestly I don't know) I simply doubt it and would prefer to see a proof if someone just claims that it is.
Given that nothing prooflike is coming over here, maybe I take the time to study Tom Gutmans sheet here: http://communities.ptc.com/message/93073#93073
Given the usual quality of Tom's articles/sheets this may qualify for a proof 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For your convince my dear friend.
Proofs etc:
http://www.maths.lth.se/na/courses/Documents/papini.pdf
http://www.sciencedirect.com/science/article/pii/0020768376900809
Hands on approach with some wire/cable data from 70s
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, this thread got so much cluttered that I overlooked your post.
Just began to flip through the first link (papini) - while more in depth than I ever wanted to dig in, its sure interesting but I didn't really found anything indicating the function family we can expect.
I found this link (its in German)
http://www.uibk.ac.at/eisenbahnwesen/Seilbahnbau_Skriptum_2012_innsbruck.pdf
but soon realized that ever so often the cateneries would be approximated by parabolas and in case of the point load the cable is assumed to be massless, meaning that our two catenaries/non-catenaries are straight line segments. This may be satisfactory for that application but is not of help in our discussion.
Not sure if I will find time and leisure to wade through the rest.
At first I was just unhappy that a problem solution should be based on an unproved and therfore unwarrented assumption but in the meantime I am pretty sure, the the exact analytical solution would not be catenaries. Mainly because of my reflections on the results of the cases ratio pointload/chainweight = 0 resp. -> Infinity. An analytical closed solution would have to include both cases and a simple catenary doesn't.
I'm still not sure where the problem should lead to and what results are being expected (minimal height of weight, maximal forces, -...?) but I guess for practical purposes very often pretty crude simplifications are made.





