Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
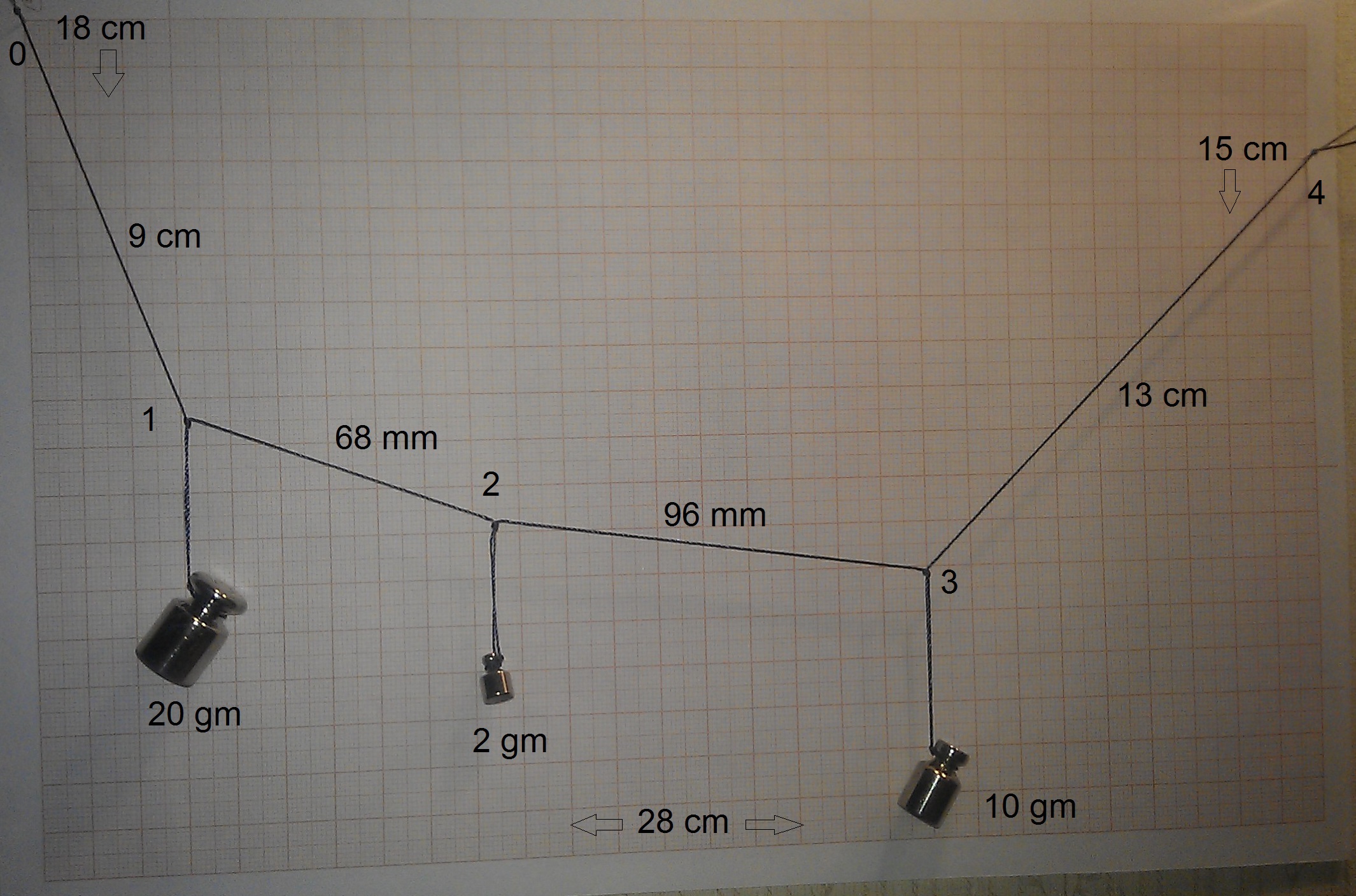
One task with 3 bobs - Forces searching
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One task with 3 bobs - Forces searching
I try to find forces in this task. The Mathcad 15 sheet is in attach. Are equations in the Given-Find block right?
What is the 8-th equation?
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The horizontal forces at the walls don't have to be equal, and
the force vector has to align with the string
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The horizontal forces at the walls don't have to be equal
If they're not equal, then the system is not static. Those two forces are the only horizontal forces acting on the system, so they must cancel out. Note that your solution has the two forces very close to each other. Remove the negative from your RHS (Valery has defined F0x as acting in the opposite direction as F4x) and re-enable evaluation of that region and your final result is pretty much unchanged.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Fred.
I think it is the solution: 4 eques and 4 unknowns:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have a solve block, and a matrix solution with the same equations; of course they have the same results!
Attached is a vector force summation at each of the three weights.
I continue to insist that the horizontal forces at the walls do not have to be equal.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, Fred! You have 8 unknown and 7 equations - change guess value an have new result!
We need one more equation!
But we can find F12 and F23 forces not in the solve block!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nope! Sorry, changing the guess doesn't change the answers:

Look at the vector solve block!!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred Kohlhepp написал(а):
You have a solve block, and a matrix solution with the same equations; of course they have the same results!
The matrix solution does not need the guess values! And same result of course.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm a bit late entering this fray on this point, but I agree with Fred. The net horizontal force is zero only if the center-of-mass(COM) doesn't move horizontally. This is clearly true in the static case, but I doubt the geometry of the strings constrains things in this manner for arbitrary angles of the various strings in a dynamic situation. In this case, there must be a net horizontal force consistent with the horizontal motion of the COM.
Lou
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solution without an animation is not solution!
But we must put TOL=CTOL-10^-7 (not 10^-): we work with cm not m - with gm not kg - it is one bug of Mathcad 15!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery,
The 4th String gets shorter and shorter.
Can this be? I don't belive that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
We do so - Pull and shorten the 4-th string!

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery likes animations. He chose L34 to be the variable that changes over time (FRAME).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Wunderbar!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think not only a fine animation but about TOL and CTOL!!! Compare pls this animation and at TOL and CTOL=10^-7 (above)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solution in Prime with compare with values from real experiment -see please the first picture in this discussion.
гс - грамм силы - gram of force
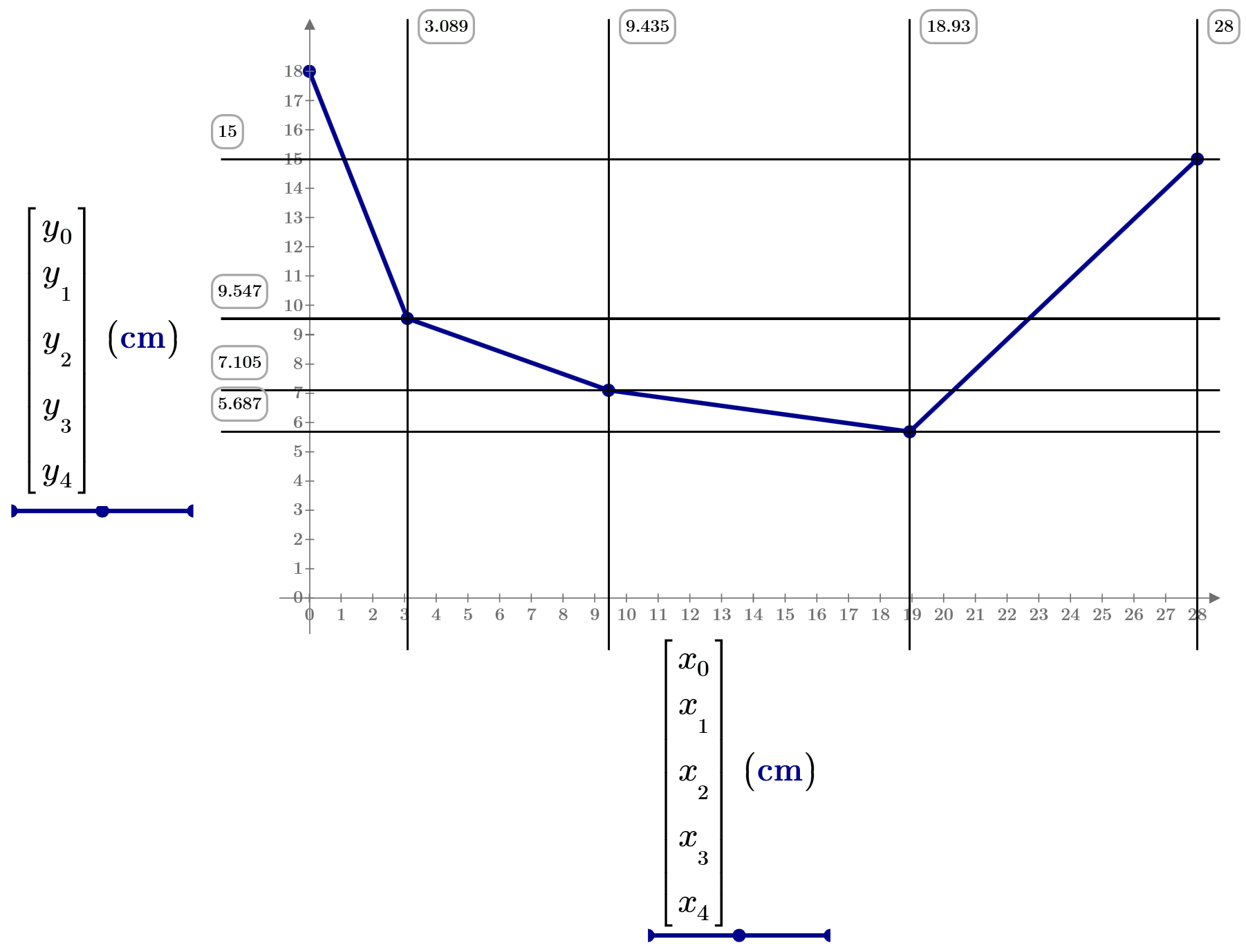
It is picture for the future article and a study for the book. Thanks to all!




- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Italia = art!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
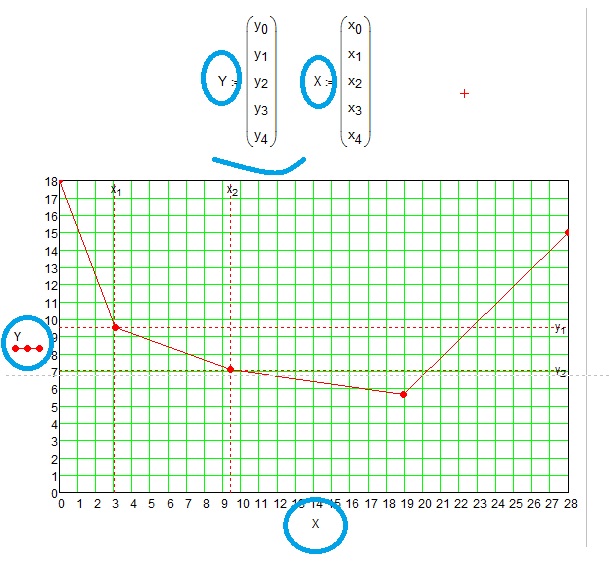
 We can use the symbolic solution for forces
We can use the symbolic solution for forces
can we have it for x and y?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
We can find F12 and F23 so!
OK?
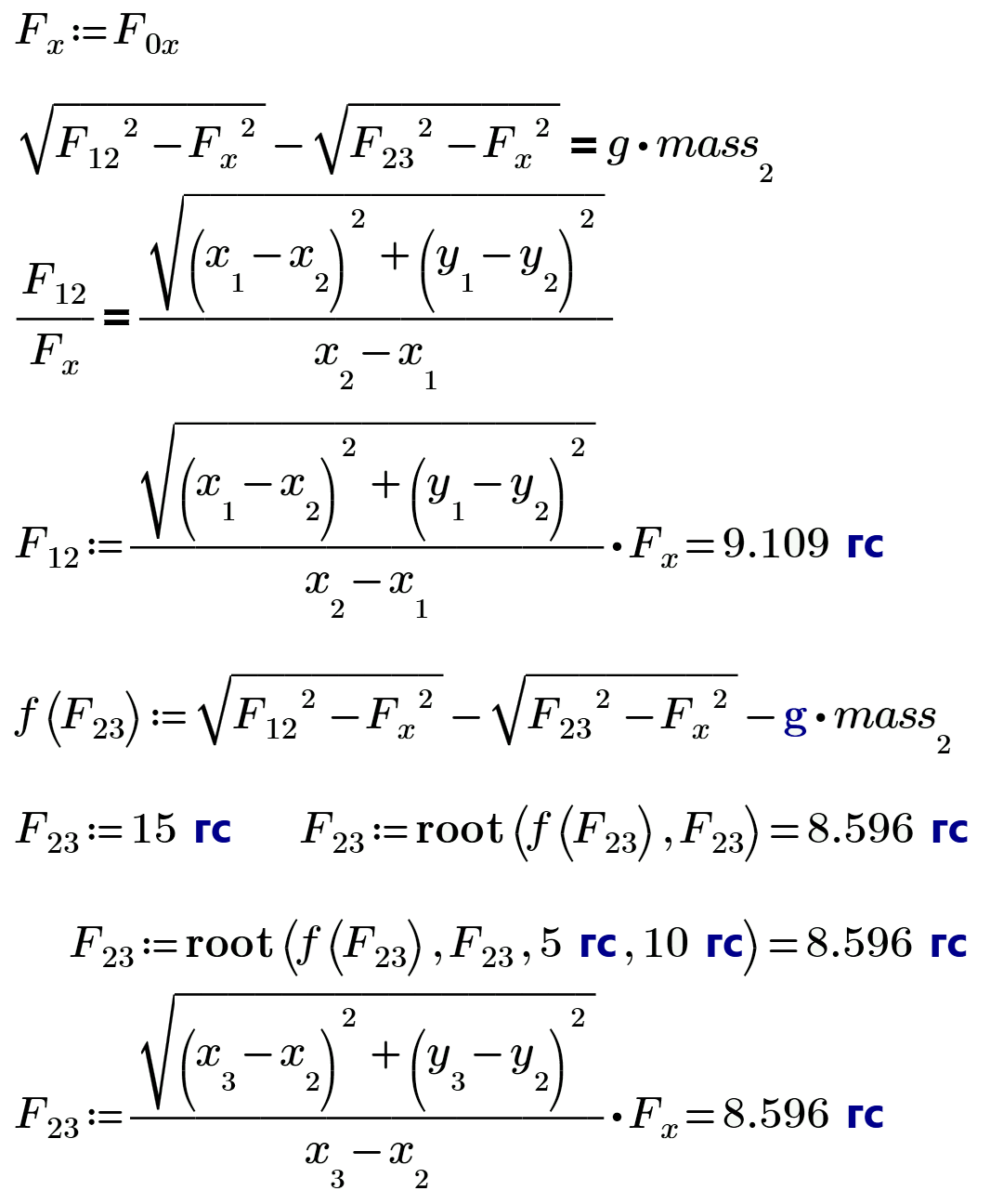
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
New task - change please Inextensible threads to tensile threads!
Слабо? With use the Hooke's law!
The sheet with Inextensible threads is in the attach!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems that we have no chance to solve the problem without the "Energy" Method which is a very elegant way to go!
Minimizing the potential Energy is what nature does make.
Thank you for giving me this to understand, Valery.
Trying to solve with Equations in the solve block with guess-Values doesn't sucess. Don't know, why.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Volker Lehner написал(а):
It seems that we have no chance to solve the problem without the "Energy" Method which is a very elegant way to go!
Minimizing the potential Energy is what nature does make.
Thank you for giving me this to understand, Valery.
I am glad to see it!
Volker Lehner написал(а):
Trying to solve with Equations in the solve block with guess-Values doesn't sucess. Don't know, why.
Attach please the sheet!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The reactions at 0 and 4 must be in the direction of the string.
For example:
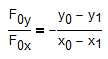
(negative required due to how your variables are defined)
You can write a similar equation for the forces at point 4.
Also, you can balance the forces in the X direction at points 1, 2, & 3, and you can balance the forces in both the X and Y directions at points 0 & 4. Some of these equations will likely be redundant (what's the mathematical term for this?).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The horizontal forces at the weights are equal (for static equilibrium.) The walls are fixed, so there is no requirement that F0x and F4x be equal in magnitude.
Yes, I was sloppy in directions so I needed a negative sign.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
I agree the walls are fixed, but look at the string. It has 5 forces acting on it. 3 of those forces are vertical (points 1, 2, and 3), so the horizontal components of the other two (0 & 4) must be equal and opposite.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery Ochkov,
This is the well known case of Funicular Polygon, extensively studied in rational mechanics.





