Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Ploting a closed curve with determined nodes
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ploting a closed curve with determined nodes
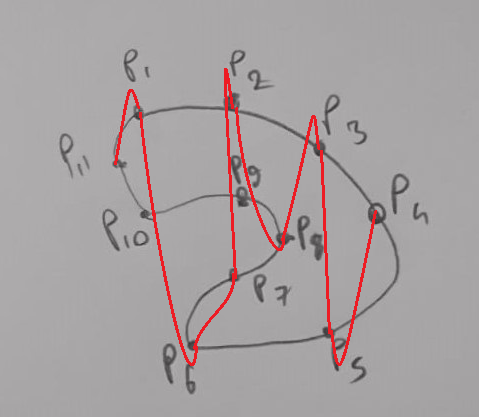
Hello everyone, I have determined 12 points individually (2D). I want to plot a closed curve between these nodes and I want to have many nodes on this pattern?
I drew an example sketch and uploaded as adding.
Apart from this, I have serious lack of education on MathCad. I need a library that I can follow each sections. I got sick of searching everything in Google. Could you suggest me a platform?
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
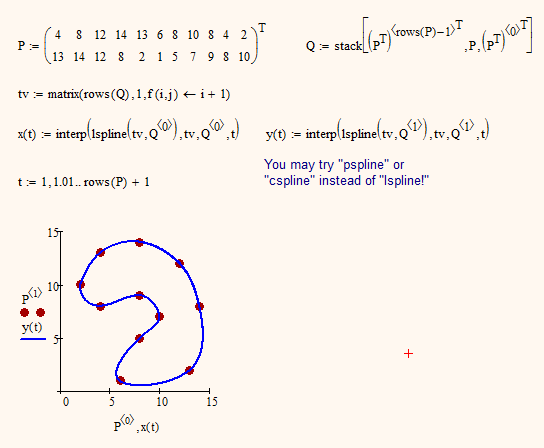
Here is a quick and not quite elegant hack using Mathcads built-in splines. Would it help?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Unless you have an idea of how to describe the relationship that defines these nodes this is going to be a long, torturous path:
- If you need a plot of y(x) vs x the existence of different values of y for the same value of x is going to be problematic. You need to "parameterize" the problem, plot x(z) vs y(z) where z is a linearly valued parameter. (You can plot a full circle as x(r,q) := r cos(q) and y(r,q) := r sin(q), with 0<q< 2 pi.)
- What the parameterized equations might be for your data is the challenge. If you know the forms of the expressions, Mathcad can find the values of coefficients that form a "best fit."
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Just 12 points? Hope you also know the order they have to be connected. You might want to look up the theory behind Bezier curves.
And no, it has nothing to do with an ellipsoid, which is a three-dimensional body and it seems all you are asking for is to connect or approximate your points with a two-dimensional smooth closed curve.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You're totally right. I edited post. I don't know why I just stuck with the wrong word. It's not even eliptical. It's like all you say: "a two-dimensional smooth closed curve"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
What you need is a cubic spline curve.
Between each pair of nodes equation is Ax^3+Bx^2+Cx+D having unique A,B,C,D
value of x and y common at the nodes
value of dx/dy same each side of nodes for matching slope
value of d2x/dy2 same each side of nodes for a smooth transition between curves
For 12 points have 12 lines each A,B,C,D for 48 unknowns
There 24 equations for x and y at the ends.
There are 12 equations for equal derivative at 12 points.
There are 12 equations for equal second derivative at 12 points.
The solution for the 48 unknowns can be done.
This can be set up in a matrix format.to solve for the ABCD's.
When they are known the figure is defined for all x,y on the curve.
Here is one prepared earlier that starts and stops away from each other. You give it end slopes at ends. It was used in real life to analyse roller coasters through designated points. It needs adjusting for closed ends..
Cheers
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@terryhendicott wrote:
Hi,
What you need is a cubic spline curve.
Between each pair of nodes equation is Ax^3+Bx^2+Cx+D having unique A,B,C,D
value of x and y common at the nodes
value of dx/dy same each side of nodes for matching slope
value of d2x/dy2 same each side of nodes for a smooth transition between curves
Did you look at his picture? How can a equation of that form work for that shape. You will wind up with a spline that drives thru his points with a single value for y for each value of x. It would look something like this:
This would be available as one of the built-in spline functions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a quick and not quite elegant hack using Mathcads built-in splines. Would it help?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This look pretty simple and nice.Thanks a lot really. I was eating my mind with the previous solution above. It works out for me if only I can attend extra nodes on this curve.
How do we create nodes automatically on curves? Let's say I'd like to have 50 nodes on the curve.
I need to have matrix that contains nodes on this curve in order to put in an equation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@tasdemirg wrote:
How do we create nodes automatically on curves? Let's say I'd like to have 50 nodes on the curve.
Werner has created a parametric graph--- functions x(t) and y(t). These will give a value of x and y (a node) for any value of t.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes I forgot to edit my message. I figured it out later when I combine it with my work 🙂 Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Werner for the trick!
But how can we use it for the problem in attach?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Thanks Werner for the trick!
But how can we use it for the problem in attach?
Not at all unless you find a way to calculate a vector of exact, not approximate, points of your curves.
Your problem is about the implicit plot of specific slices of a surface in 3D.
Its very sad that Mathcad never learned to plot implicit functions. Maybe the routines of uno (Viacheslav N. Mezentsev) can help again (we talked about them in another thread a longer time ago). But I think his algorithms are better implemented in SMath.