Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Plots for Conditional Function
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Plots for Conditional Function
Hi
I am a beginner in Mathcad Prime. I would like to make plot for under stated conditional function .Please help in this regard.
V(t)= 5 for 0<t<5
=-5 for5<t<10
It should be square wave plot with period 10. I mean after t=10 it should repeat itself.
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
SAMEER GARG wrote:
Please find final outcome as per your suggestion
Are you sure about your equations? I'm not sure they will give you the minimized value you are possibly seeking.
A few comments.
You have defined I1 and Vripple_min to be functions; this means you cannot put an evaluation operator (=) after them - this is in part what Mathcad is complaining about.
It's usually well worth while evaluating functions at a few values (especially critical ones) and/or plotting your functions to check if they make sense over the intervals of interest.
I'm surprised Mathcad let you type in KHz instead of kHz; the SI multiplier for 1000 (kilo) always has abbreviation 'k' not 'K'. Indeed, 'K' is often used in computing circles to mean 2^10 = 1024 (eg, KB).
It helps others if you post your worksheet - saves all that typing and there are sometimes problems with a worksheet that aren't obvious or visible from a screenshot.

Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
Thanks for your response. I have been through your way but i am not able to plot the attached expression. Can you please tell where i am doing mistake?I am expecting a periodic square waveform toggling between +/-24V with on and off period 5us.
Here I used Ton,Toff as a cons; x as a variable and Vlp(x) as a function

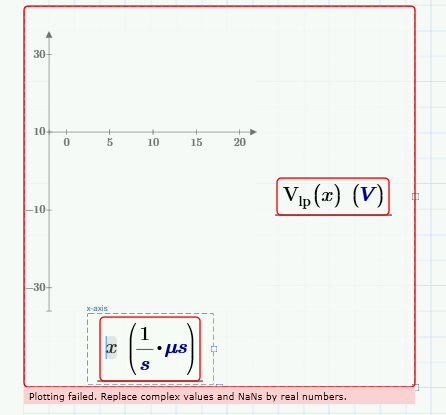
Regards
Sameer
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sameer,
The error message points into the direction of something undefined (NaN stands for Not A Number).
You are plotting Vlp versus x, but haven't defined x. That means it (probably) defaults to the range -10 to 10. The first problem you definition of Vlp then poses is what to output for x=-10 (or any other negative of x). So you have to fix that. Either by defining x to have only positive values, or (better?) by including output for negative values of x in the definition of Vlp.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes wrote:
Sameer,
The error message points into the direction of something undefined.
You are plotting Vlp versus x, but haven't defined x. That means it (probably) defaults to the range -10 to 10. The first problem you definition of Vlp then poses is what to output for x=-10 (or any other negative of x).
Success!
Luc
Hi Luc,
I think Sameer's question has been addressed in this thread (one of three asking the same question plus one on Eng Tips): Periodic Function Plotting
The function needs units adding to the constants in the if clauses and the x in Vlp(x) needs multiplying by microseconds (or x needs to be defined in terms of microseconds and microseconds put in the x-axis placeholder)..
It should be possible even in Prime 3.1 to limit the x-axis range to a minimum of 0, hence negating(!) the need to address negative values.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah, I forgot to scroll down to the end of the list.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks StuarBruff
I substitute the unit of each range variable in terms of us. Now it works and giving results what i was looking for. Sorry for repeating the question in thread![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
SAMEER GARG wrote:
Sorry for repeating the question in thread
No worries. It can be frustrating for new members when they're trying to get an answer to a problem they really want solving and nobody answers (or they don't give beginner's answers!). It's just one of those bits of forum etiquette that make life less frustrating in the long run. ![]()
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But you have more problems in your definition of Vlp. Note that Ton and Toff are the same, so what will come out of the test if Ton<x<= Toff? This only occurs when x=Ton(=Toff).
Then whenever x>Toff you let the result be Vlp(x-Toff), which means that for x=1.5*Ton (=1.5*Toff) you get the same result as for x=0.5*Ton.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Unfortunately using mod() to make the function periodic will fail for negative arguments. This is because the mod() function is implemented in such a way that it will return negative values for negative arguments -> mod(-12,5)=-2 (and not 3).
You can cope with that problem by either overwrite the built-in mod() function with one of your own or by applying mod() twice (after adding the period T after the first mod().
Here is a different way to define a piecewise function using the programming if statement instead of the if function. If you are using Prime Express or intend to create worksheets for Express, you have to use nested if-functions as programming is a premium feature not available in Express.
Furthermore I show three different ways to make a function periodic. The last one, using recursion, is in no way recommended and is only there as for academic interest.
It was created in Mathcad 15 but I see no reason why it shouldn't work the same way in Prime, too.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Unfortunately using mod() to make the function periodic will fail for negative arguments. This is because the mod() function is implemented in such a way that it will return negative values for negative arguments -> mod(-12,5)=-2 (and not 3).
Furthermore I show three different ways to make a function periodic. The last one, using recursion, is in no way recommended and is only there as for academic interest.
It was created in Mathcad 15 but I see no reason why it shouldn't work the same way in Prime, too.
True. Why they implemented trunc mod instead of floor or, preferably, Euclidean mod, is beyond me.
... Furthermore I show three different ways to make a function periodic. The last one, using recursion, is in no way recommended and is only there as for academic interest.
Oy, oy, oy. What is it it with you and recursion, already, Werner? Did it steal your hubcaps or forget to feed the cat? Or does it still owe you 10 euros? ![]()
Recursion is generally fine for many applications and its performance isn't too far off it its iterative counterparts. If an algorithm is easier to implement or makes more sense (to me) done recursively, then there's usually no significant penalty. It's generally only with poorly designed recursive algorithms, deep recursion and Mathcad's hard-wired recursion depth that problems will occur. Indeed, one of the problems I have with Prime is that it doesn't allow local recursive functions, and that means I've either got to rewrite them in iterative form or have a superfluous external recursive function, and it's usually just not worth the effort of rewriting them.
With your definition of f3 and the number of cycles, it will hardly present a problem. It will probably do around 800-900 cycles before you start to notice any performance hit.

Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe recursion owes me more than just 10 Euro in the meantime 😉
Honestly I like playing around with recursion but when it comes to permanent implementation I'd usually prefer an alternative for performance and stability reasons.
But I agree that in this case I, too, don't see much reason not to use the recursive approach other than the small performance advantage of my second version.
I am surprised that the non-periodic f_0 is performing that bad when you did the timing. I tried, too, and f_0 would outperform all the others.
I also introduce a new fourth variation which simulates what the recursive variant does using a while-loop but the gain in speed was by no means noteworthy. I would have thought that getting rid of multiple function calls, bulding up recursion stack would have a bigger effect.

WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Maybe recursion owes me more than just 10 Euro in the meantime 😉
And the moral of this sad tale is "Never lend money to recursion". borrow(money):=money+borrow(money) ....
Honestly I like playing around with recursion but when it comes to permanent implementation I'd usually prefer an alternative for performance and stability reasons.
With the speed of modern processors - although see my timings later! - I usually don't worry unduly about performance, as the elegance and simplicity of the recursive solutions usually outweighs any performance hits. For most "divide and conquer" type algorithms the chances of getting anywhere near the recursion depth limit (about 9000 I think) is negligible. Needless to say, I've hit the limit in a few cases! 🙂 This usually happens where I'm effectively using recursion in place of iteration (eg, tail recursion) and it is something I wish PTC would address properly. I don't know what Prime does, but Mathcad 15 compiles a worksheet down to something called the Mathcad Programming Language, which looks like a variant of Haskell - and that definitely can handle recursion in an efficient manner!
But I agree that in this case I, too, don't see much reason not to use the recursive approach other than the small performance advantage of my second version.
I am surprised that the non-periodic f_0 is performing that bad when you did the timing. I tried, too, and f_0 would outperform all the others.
I also introduce a new fourth variation which simulates what the recursive variant does using a while-loop but the gain in speed was by no means noteworthy. I would have thought that getting rid of multiple function calls, bulding up recursion stack would have a bigger effect.
You'll find that that the difference will show up with more cycles. The function won't actually go recursive until t changes to next cycle, so for just the few in the -10..15 range, the effect of saving the environment will be hardly noticeable. However, the time increases approximately linearly as the number of cycles increases whilst keeping the number of points constant (in contrast, the iterative versions have approximately constant time)

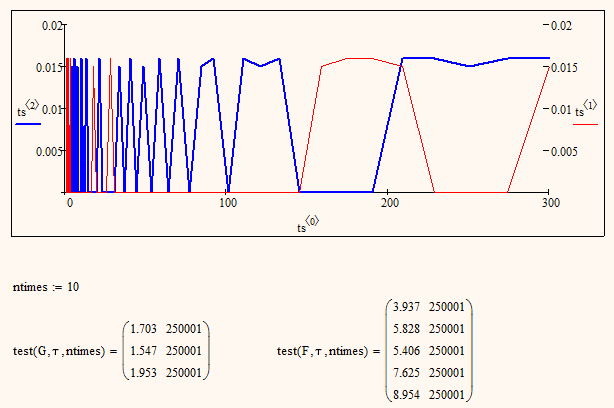
I've added your new function to the worksheet and a new variant of the g function, plus a replacement floor-based mod function. I also created vectors for each group of f and g function and used a small program to iterate over each function vector. Here are timings:

This is on an i7 with 8 GiB RAM; Amusingly, I got about half the time on my other laptop which has a Core2Duo with 4 GiB ...
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Timing values are amusing, indeed, and I am not sure if thats due to the imprecise time() function.
After all, here is what I see when I load and recalculate your sheet with an old single core (Intel Pentium M, 2 GHz) notebook with just 1 GByte of Mem under Win XP

The next recalc gave me this:
Just forgot to mention:

😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The question seems to come up quite often.
I just found a Prime 3 sheet which I posted some time ago as an answer to someones question.
There I turned the first two methods to make a function periodic into convenient functions. Maybe its of help to you, too. The meaning of the arguments should be obvious.

EDIT: And now I also found the thread the file belongs to: Re: Repeating periodic function
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am confused and maybe you can help me.
Is there anything new in your file which LucMeekes did not show a day ago?
BTW, I considered the question to be of a more general nature, the square wave being just an example.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your response but as i told i am beginner in Mathcad Prime so I was looking for some basic format. Sorry but i scared by seeing the solution in terms of Mod(), floor() etc. After googling i got may be understated expression can solve my problem for the time being
![]()
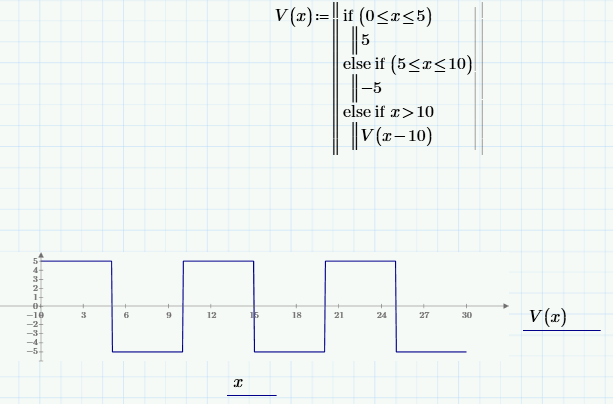
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
SAMEER GARG wrote:
Thanks for your response but as i told i am beginner in Mathcad Prime so I was looking for some basic format. Sorry but i scared by seeing the solution in terms of Mod(), floor() etc. After googling i got may be understated expression can solve my problem for the time being
E
Yes, it will. Provided you don't want to use more than a 100 or so cycles. After that you will find your calculations start to take longer as you have, in many people's estimations, strayed into a far scarier territory than mod and floor ... Recursion!
For every cycle (multiple of 10) beyond the first one, the function V calls itself. This means the software will save its current working environment (eg, list of variables) in memory so that it can evaluate the "new" version of V. After calculating the final V, Mathcad then has to restore all of the saved environments in turn until it gets back to the normal working level. All of this takes time.
It's better to get to grips with understanding mod, floor, ceil, trunc and the other rounding functions. You will find they can make life considerably easier when doing numerical work.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
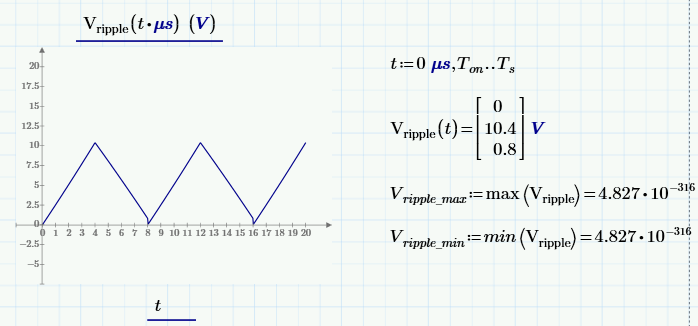
Hello Everyone
Thanks for your kind response. I would like to calculate max and minima of any function. I was going through Max and min function but i was getting some unpredictable answer. Please help in this regard.
Note: It is a part of system so all variables are defined previously.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Try
"max(Vripple(t))"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred Kohlhepp wrote:
Try
"max(Vripple(t))"
I'm not sure that will give the desired result - t is a range variable, so max should return the "maximum" (ie, the only) for each value of t.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It appeared (to me) that Vripple(t) resulted in a vector:
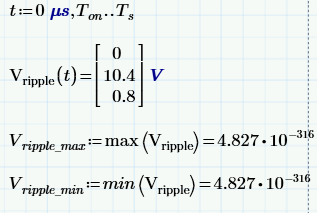
which is why I suggested using it inside max() and min(). You are (of course) correct--if it's not a vector, it won't work.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred Kohlhepp wrote:
It appeared (to me) that Vripple(t) resulted in a vector:
which is why I suggested using it inside max() and min(). You are (of course) correct--if it's not a vector, it won't work.
I think it's a case of Prime's output looking deceptively vectorish, Fred.

It might be better if Prime could distinguish between range expansion and arrays, eg (but probably not!)

Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
SAMEER GARG wrote:
Hello Everyone
Thanks for your kind response. I would like to calculate max and minima of any function. I was going through Max and min function but i was getting some unpredictable answer. Please help in this regard.
Note: It is a part of system so all variables are defined previously.
min and max apply to arrays only; they don't find the maximum or minimum of a function - V.ripple in this case. In fact, I'm surprised they don't flag up an error (as they do in Mathcad 15) rather than returning what looks like a very small 80-bit floating-point number (or one of the other IEEE special formats).
You have several choices: create a vector and take the max/min of that (note that the actual max/min of a cycle may lie between the values you compute), or use the maximize/minimize functions or simply analyze your function and calculate the max/min (you may be able to do it symbollically).
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For functions "seccionalmente contínuas", o "contínuas a trozos" (can't remember the english name) I'm more comfortable with this implementation, because can handle symbolics, even the derivative isn't a function (is a distribution, but the integral is function). This is specially useful, for example, calculating deflections for beams.
I try to do this in Prime, but can't. In Prime Phi = Greek F = Heaviside evaluate at 0 gives ... Phi(0) = 0.5. That's a serious, serious bug.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alvaro - first let me say that I appreciate your work and that I am glad you are back in the forum.
Concerning the implementation of the Heaviside function, the behavior seems to have changed since MC11 as in MC15 we already have it this way:

And thats not a bug, its done on purpose that way as you can read in the help

Its a quite usual convention and sometimes called the half-maximum convention.
See here Heaviside step function - Wikipedia, the free encyclopedia or here Heaviside Step Function -- from Wolfram MathWorld
There is also a more general convention (I couldn't find a reference in the net at the time) where Phi(0)=c with c element of K. And K denotes any arbitrary set of numbers containing 0 and 1.
But when I first used Mathcad's Phi function in the "newer" (past MC11) versions, I was surprised, too, as I was not aware of this convention either.
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Alvaro - first let me say that I appreciate your work and that I am glad you are back in the forum.
Concerning the implementation of the Heaviside function, the behavior seems to have changed since MC11 as in MC15 we already have it this way:
Not in MC11:
And thats not a bug, its done on purpose that way as you can read in the help
Your help, not mine (Prime 3.1)
Maybe best value for Phi(0) is ... undefined. See maple:
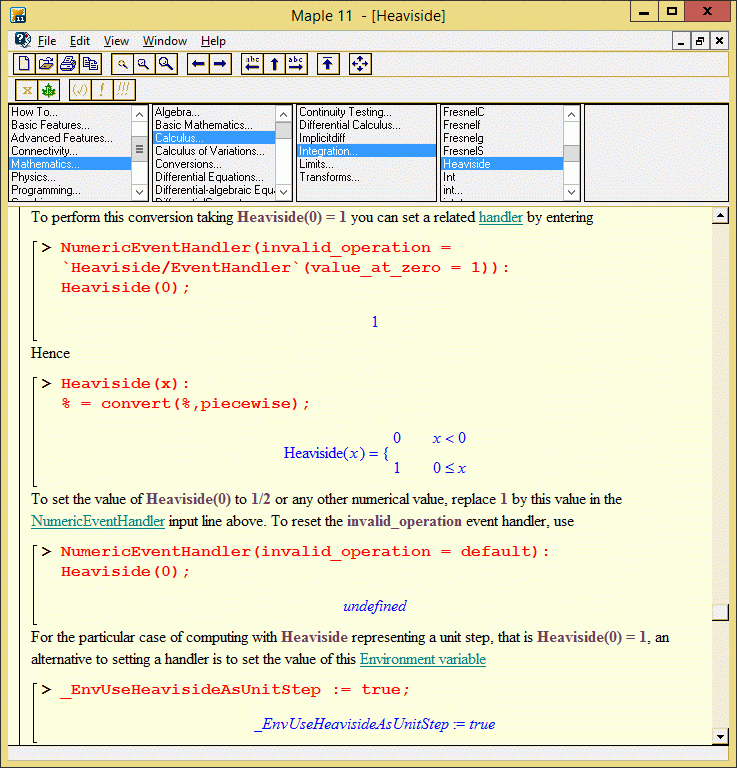
If Heaviside go to be the unit step, must to be set equal to 0 for x=0. If not, have not Unit Step. And then, can't diff or integrate "seccionalmente contínuas" functions. Theoretically, UnitStep is very important. For example: any homogeneous linear system can be determined by the answer to the pulse and the unit step. And can't construct intervals, certainly. At less, not in an elegant form.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
...
Concerning the implementation of the Heaviside function, the behavior seems to have changed since MC11 as in MC15 we already have it this way:
I guess that must to be in MC14, which have mupad, because MC13 have maple. Mupad doc's says that Phi(0) = 1/2. I don't like nothing this value.
Best regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlvaroDíaz wrote:
I guess that must to be in MC14, which have mupad, because MC13 have maple. Mupad doc's says that Phi(0) = 1/2.
Phi is (also) a pure numeric function which does not depend on the symbolics. But its quite possible that they changed the value just beacause Mupad defines it another way.
I don't like nothing this value.
Neither do I 😉
Regards Werner







