Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Plotting Points ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Plotting Points ?
Hello, Everyone.
From :
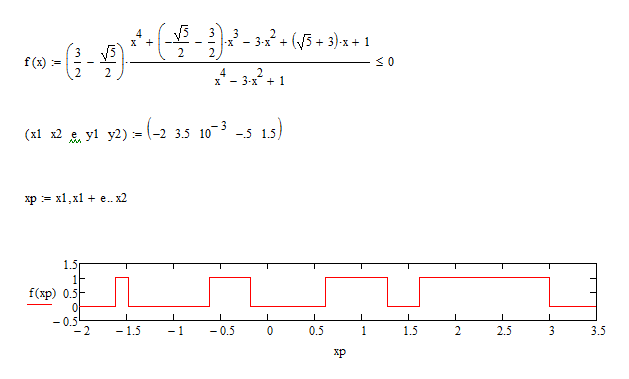
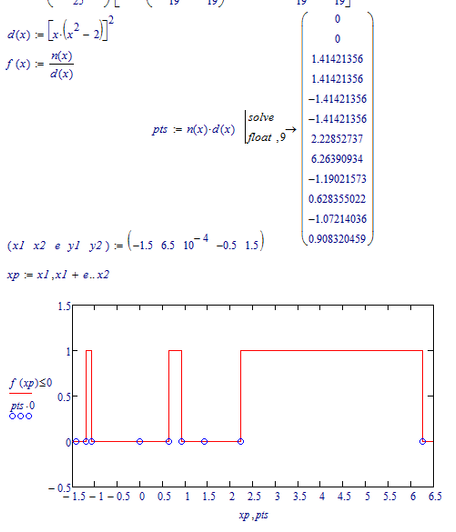
How to plot 8 upper-corner-points ?
Thanks in advance.
Regards.
Solved! Go to Solution.
- Labels:
-
Math Homework
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your method to solve it, this is a new to me ! ![]()
![]()
![]() Many thanks for your time and help, Luc. I got it.
Many thanks for your time and help, Luc. I got it. ![]()
![]()
![]()
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc, I don't know the reason the plot doesn't show up in this case.
Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have disabled the plot region!
Right click the plot region and chose "Enable Evaluation"
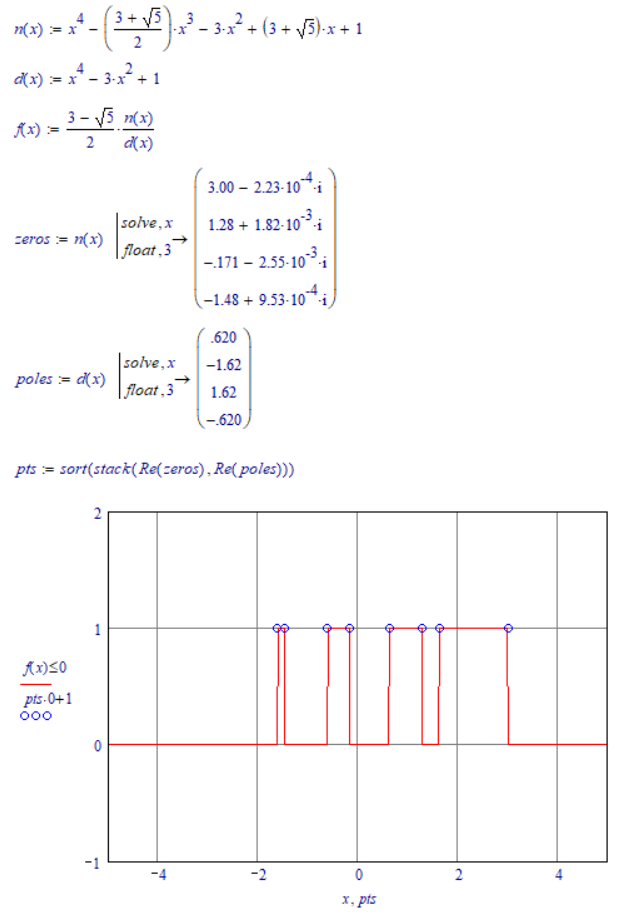
As you can see the poles at +/-sqrt 2 and 0 are no valid solutions to your problem this time. This is because they are poles of second order (the square in d(x)) and so there is no change of signs at those positions. A sign change only occurs at poles of odd order.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Many thanks, Werner. And how to keep the same "procedure" and eliminate 3 points are not 6 lower-intersection-points ? ( maybe just edit ? ). ( And how to plot local minimum-points of the f(x) ? )
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Correction : plot local minimum-points of the f.0(x)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@lvl107 wrote:
Many thanks, Werner. And how to keep the same "procedure" and eliminate 3 points are not 6 lower-intersection-points ? ( maybe just edit ? ).
You may think beforehand and don't ask for the zeros of the denominator which are of even order. In your example obviously all are of even order and so you would not ask for d(x)=0 at all.
As an alternative you may consider writing a function which eliminates all points of zeros (nominator and denominator separately) which occur an even number of times. This routine also must consider removable discontinuities like when nominator and denominator have a common zero. Good luck!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
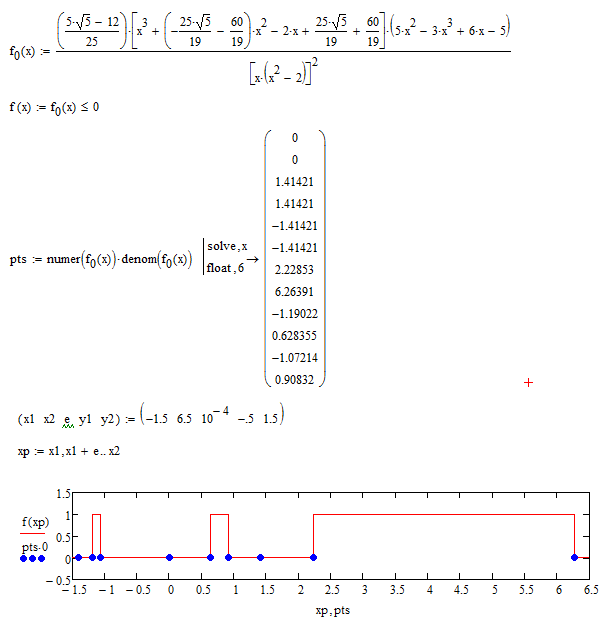
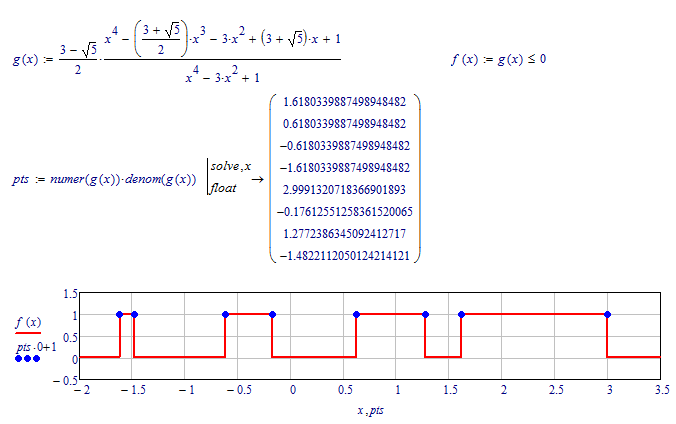
Luc, after I have got all of your hints, I try to plot all lower-intersection-points of logical-plot, but I don't know it's true for all of cases :
Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
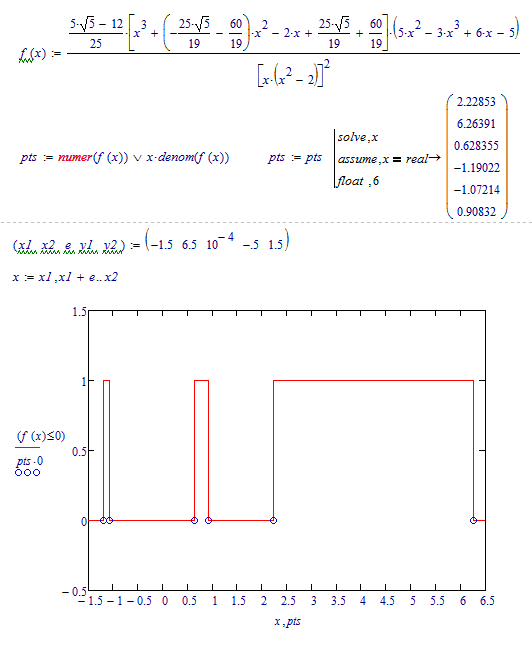
Hi,
You could also use the "numer" and "denom" functions as shown:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
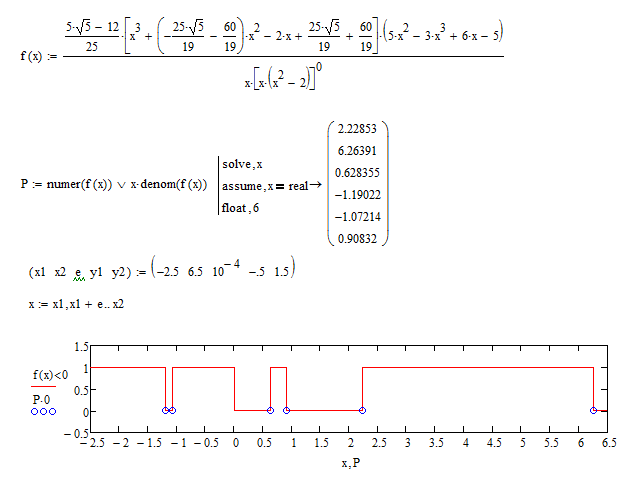
or more compact:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
F.M. and Werner, with your "procedures" above, It seems that I just need "input" a new function ! ![]()
![]()
![]() :
:
Many thanks for all your time and help.
Regards.