Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Polar and Cartesian Plots
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Polar and Cartesian Plots
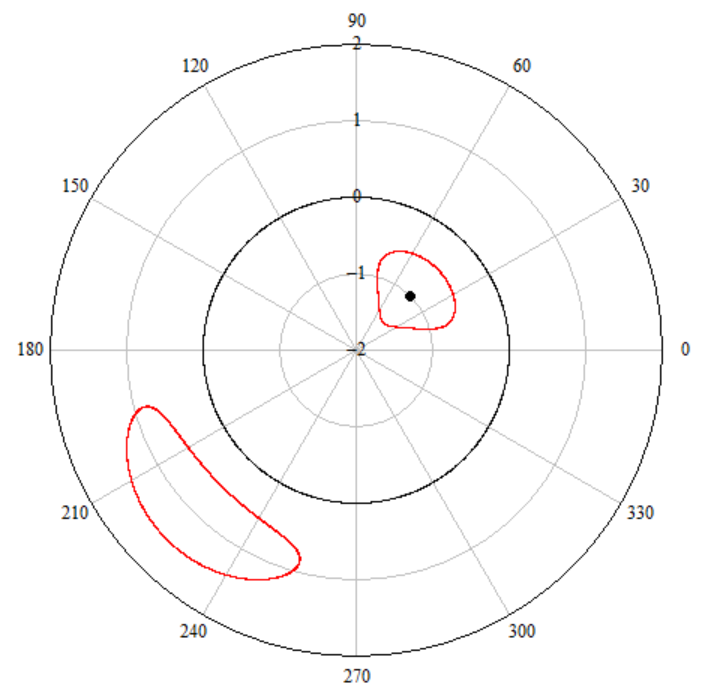
Can you create the curve in X-Y plot?

More simple curve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Showing negative radii in a polar plot is a feature which should be handled with care.
In case of your cardioide its just an offset by 1 so its easy to do an xy-plot

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger написал(а):
Showing negative radii in a polar plot is a feature which should be handled with care.
Thank, I know it.
And what about question?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank, I know it.
And what about question?
It didn't look that way.
Your question was "Can you create the curve in X-Y plot?" and as you could see obviously the answer was yes.
The other two pics don't show any information, so I don't care.
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery.
Any relationship that you have as rho = rho(phi) can be converted to cartesian using pol2xy, or they expression with radicals and atan2 function.
Best regards.
Alvaro.
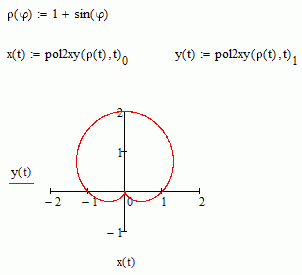
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess Valery wanted to tease us as he showed an equation (r(x)=sin x) which normally would yield a circle but because he switched "show negative radii" on, we see a cardioid and it was necessary to change the equation to r(x)=1+sin x before plotting it in cartesian coordinates.
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
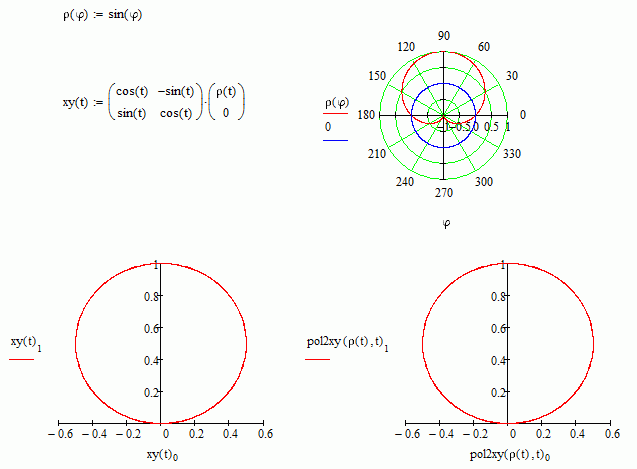
Hi Werner.
I see. And can't get it as the usual procedure: take the point rho(phi) along the polar axis, to right if positive, to left if negative. Then rotat it a phi angle.
But this gives the same points than pol2xy. Can't see how to "open" the cartesian xy plot to give "space" to those values.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its tricky. The six polar plots below are all the same formatted (negativ radii is on). The only difference is that I set the minumum value of r to different vales.
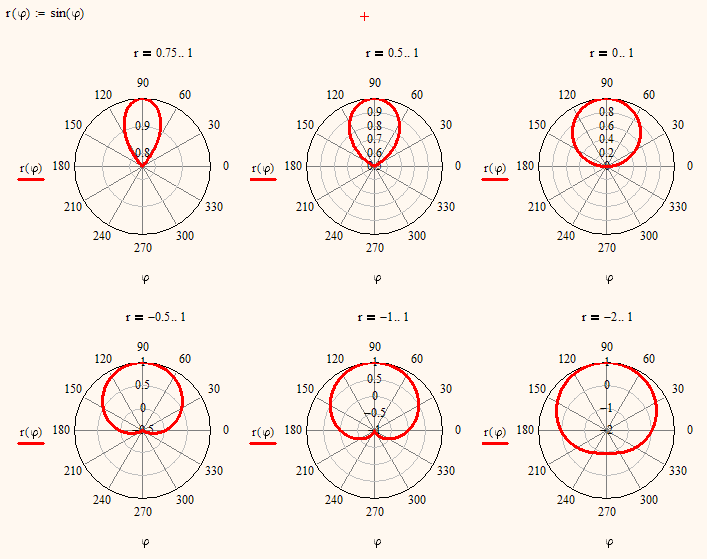
Now we can simulate the same in an xy-plot, but we get more than we want 😉
In my answer above I forgot to scale.

Regards
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
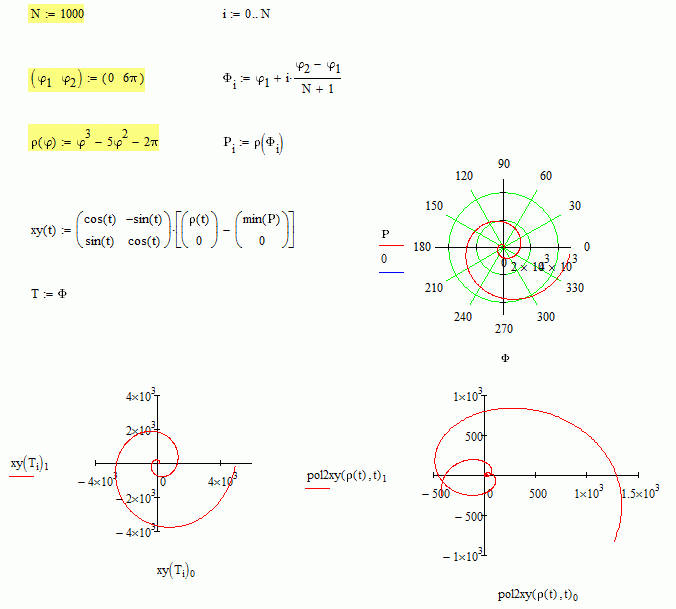
So, I guess that, without manual setting the axis limits, attached can draw the same path into xy plot, given one in the rho-phi plot. Simply must to know the minimun for the rho range.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
r.min seems to be 0 or close to) in your example.
I think otherwise we still need the scaling factor 1/(r.max - r.min)
Regards
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi.
Actually, it is -24.8. It is not a simple spiral. Check the attached, I guess that it is not necessary to scale the function for get the same path (if don't touch the axis limits).
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, I see. You are right.
I needed the scaling just to get a consistent size of the xy-plot to compare with the polar plot. But that way I get different size than in polar.
I agree that it should be done w/o scaling.
BTW, why not just
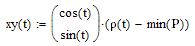
or did you experiment with different transformations?
Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner.
Yes, I try others, but this looks more instructive, because shows the manual procedure to make polar plots. Others are this which you show, or directly with cos and sin directly for x,y points. The other that can be view as interesting could be with complexes: define z = (ρ(φ) - min(Ρ))*exp(i*φ)). Then x = Re(z) and y = Im(z) gives also the same path.
Also I'm convinced that, as plotting is actually a numerical procedure, there are no way for replicate this plots without using a range to calculate the min for the rho values.
About other developments, can check this: Polar plot using Excel component
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I could be wrong, but I actually thought Valery was proposing a challenge to determine what functions he shows in the second two polar plots. However, rather than posting the equations, he wants us to post a cartesian plot. The first, I assume, was shown as an example.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Mark.
Richard Jackson have the answer!
Some time ago, I ask for interpolate some turbine plots, the shaft over rpm, and things like it. Plots that I post in this time, was taken from the web or from API books, but because the actual turbine data which I funally use is property of the manufacturer, I don't preserve the files where the interpolation was done, that's for avoid mistakes from my side.
But Richard have implement an automation for call spline2 and tracer, a small software to capture points in a jpg plot.
Also he develop the images procedure to automatically extract, from a picture component, the points and then interpolate it with image process functions.
So, with those files, I guess that the general problem of get the Valery's pictures as functions could be done with those procedures, at least in the way of splines in two dimensions, or spline2.
Best regards.
PD: Tracer was a free software, but Richard owns other similar, proprietary, which can scan points in polar plots too.
Edited: Here Re: Extract data from chart it is the Richard's file: https://www.ptcusercommunity.com/servlet/JiveServlet/download/249904-70287/Digital%20Image%20Function%20Analysis.zip
Edited2: Oh, original Spline (for spline2 interpolation) function in two dimensions, was from ... Valery!.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Another way: Component which replicate Tracer utility (finally I found it here): Unplotting tool .
Valery don't be specific about if he want the analytical expression. Actually, splines have their own "analyticity".
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mark Gase написал(а):
I could be wrong, but I actually thought Valery was proposing a challenge to determine what functions he shows in the second two polar plots. However, rather than posting the equations, he wants us to post a cartesian plot. The first, I assume, was shown as an example.
Thanks, Mark!
It was my question!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I was successful in understanding the question. However, don't count on me for a solution. ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The second curve is a.... circle (red) with blue R - see please the picture and the Mathcad 15 sheet in attach. The first one - the first.
What is it a second branch?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
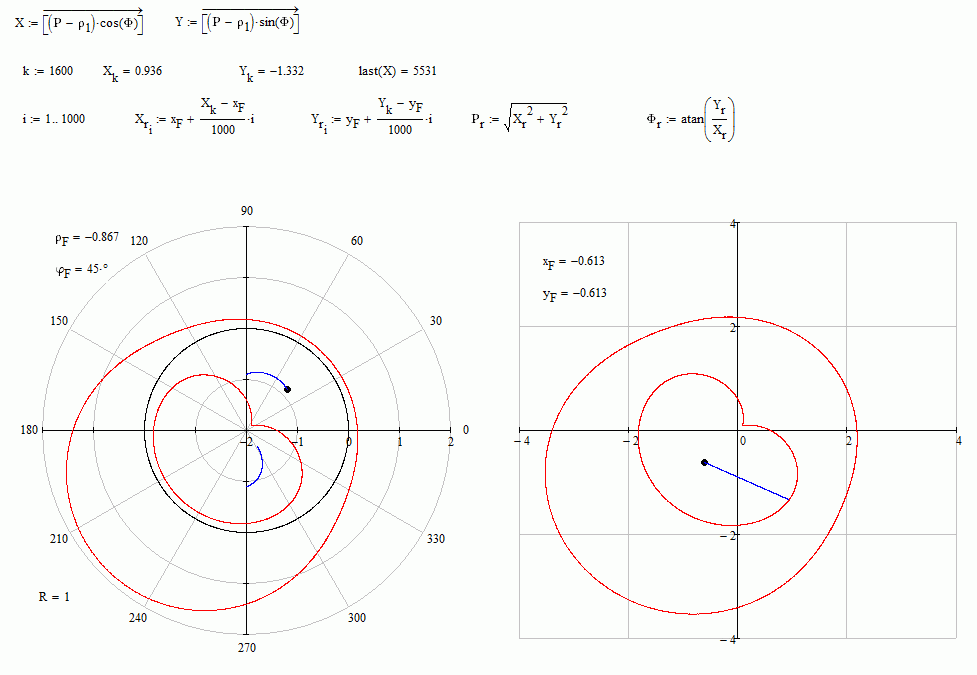
Hi Valery
Valery Ochkov wrote:
The second curve is a.... circle (red) with blue R - see please the picture and the Mathcad 15 sheet in attach. The first one - the first.
What is it a second branch?
I guess that enabling negative values for rho what actually plot isn't the original function, but a rho - min(all rho's) versus phi, in polar coordinates, and the equivalent path for cartesians, as this picture shows.
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
We have two branches of hyperbola. But may be we have two branches of circle and ellipse etc
two 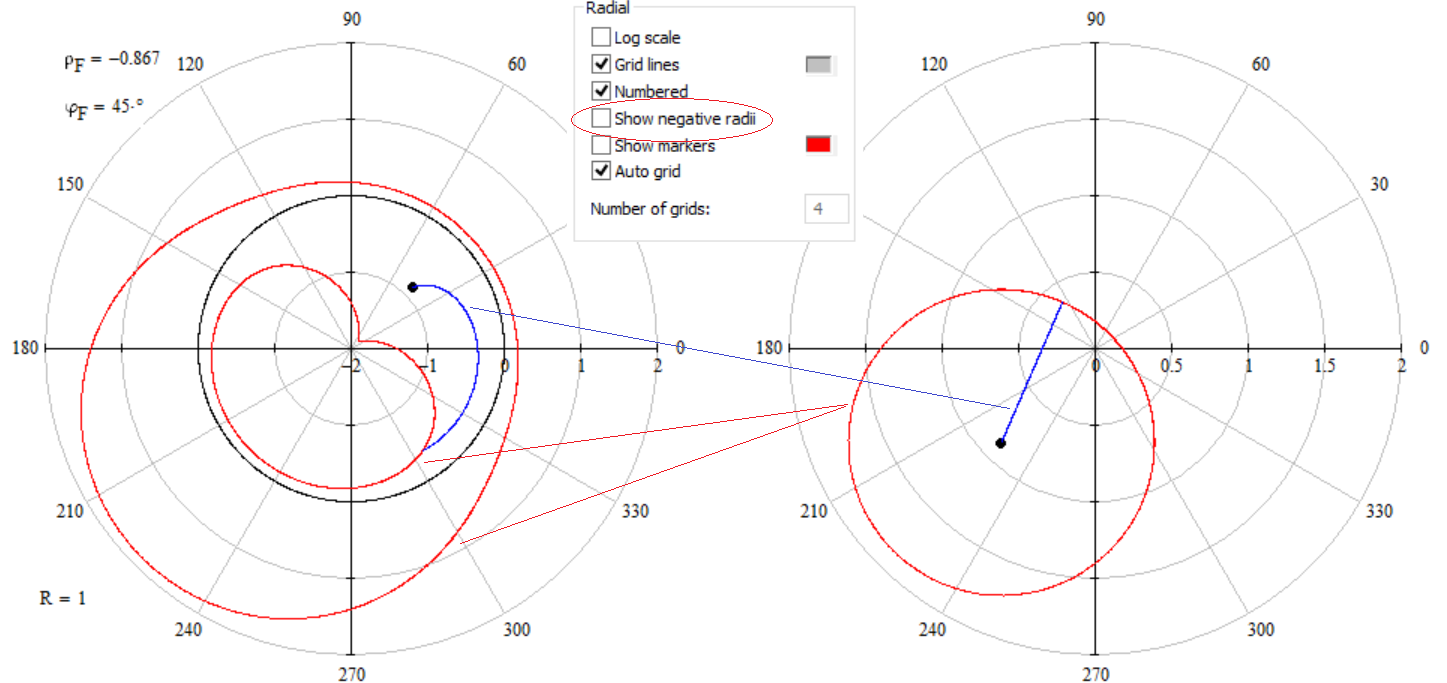
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery.
We have, but with complexes. In the complex plane amazing things happen. Log and exp are periodics, the true limit for expansion series was reveal, and ... ellipses and circles have some kind of branches.
But while the hyperbola branches are open to the infinity, those others are closed and isolated. Mathematicians don't like those, because they seems to be not analytical.
So, I see no hope for convince them to consider that as extensions of the curves, unless you can extend in some way the analyticity of them.
Analytic function - Wikipedia, the free encyclopedia
Best regards.
Alvaro.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad Prime has negative radii too






