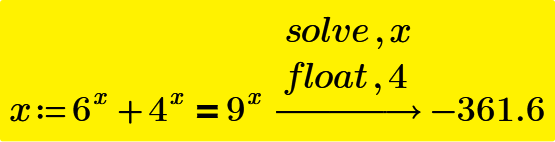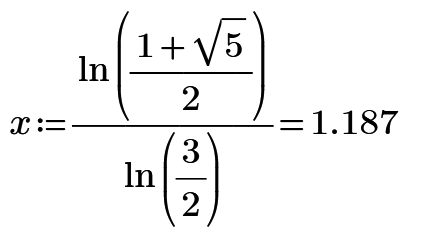Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Prime 7 symbolic bug of solve 2
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime 7 symbolic bug of solve 2
Is this a Prime 7's symbolic bug of solve? The answer I want to get is shown as follows.
Solved! Go to Solution.
- Labels:
-
Puzzles Games
- Tags:
- Prime_7.0 Bug
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Guess you get a different result if you omit the modifier "float,4", right?
The symbolic engine in P7 was changed by PTC from MuPad to Axiom for business reasons (to avoid having to pay license fees to Mathworks) and not because it would be an improvement. So its no surprise we see so many errors and incapabilities of this new engine posted here in the forum since the release of P7. There were also posted bugs in Axiom which were detected in P6 and I don't know if any of them already got fixed in P7.
As usual you can either just live with this inability, or find a workaround and, if you are very optimistic and feel it could help, you may open a support case at PTC and report it, hoping the engine will be improved in a future version.
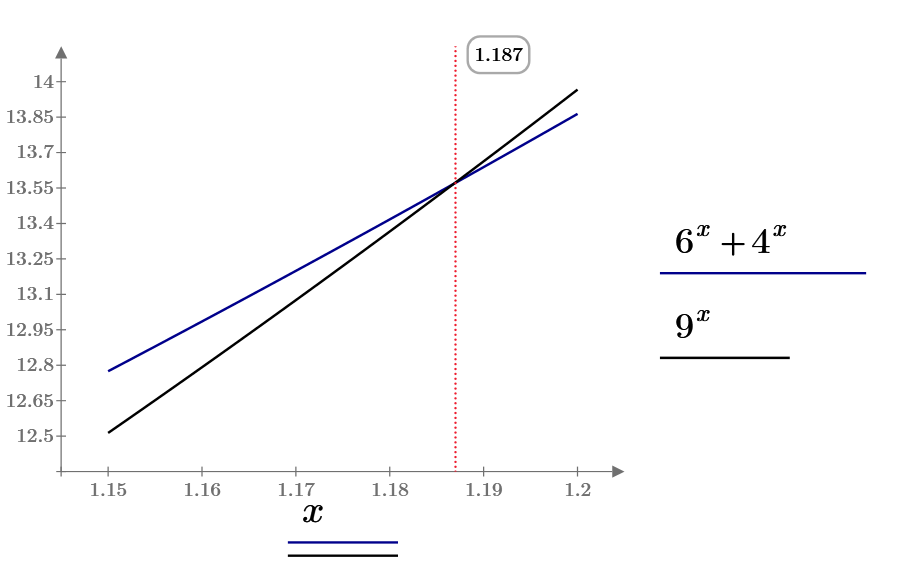
In MC15 you get the solution you expect, but even without the "float" modifier it will only give a numeric solution. As you can see in the pic it needs a lot of help to be able to calculate the exact solution:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Guess you get a different result if you omit the modifier "float,4", right?
The symbolic engine in P7 was changed by PTC from MuPad to Axiom for business reasons (to avoid having to pay license fees to Mathworks) and not because it would be an improvement. So its no surprise we see so many errors and incapabilities of this new engine posted here in the forum since the release of P7. There were also posted bugs in Axiom which were detected in P6 and I don't know if any of them already got fixed in P7.
As usual you can either just live with this inability, or find a workaround and, if you are very optimistic and feel it could help, you may open a support case at PTC and report it, hoping the engine will be improved in a future version.
In MC15 you get the solution you expect, but even without the "float" modifier it will only give a numeric solution. As you can see in the pic it needs a lot of help to be able to calculate the exact solution:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Still a better numeric solver than symbolic.
There's always root()