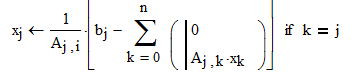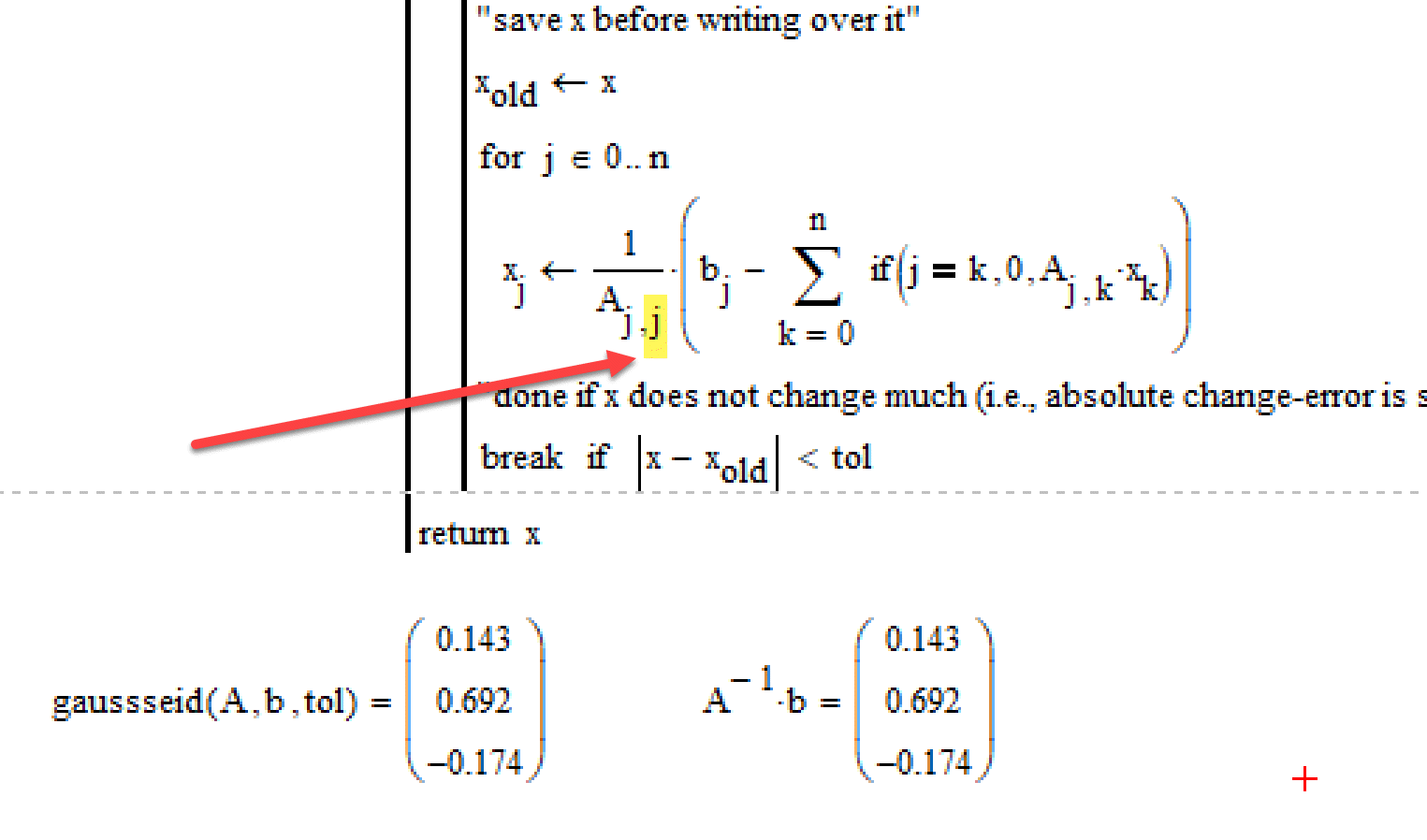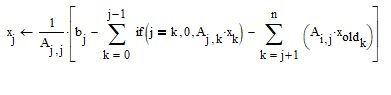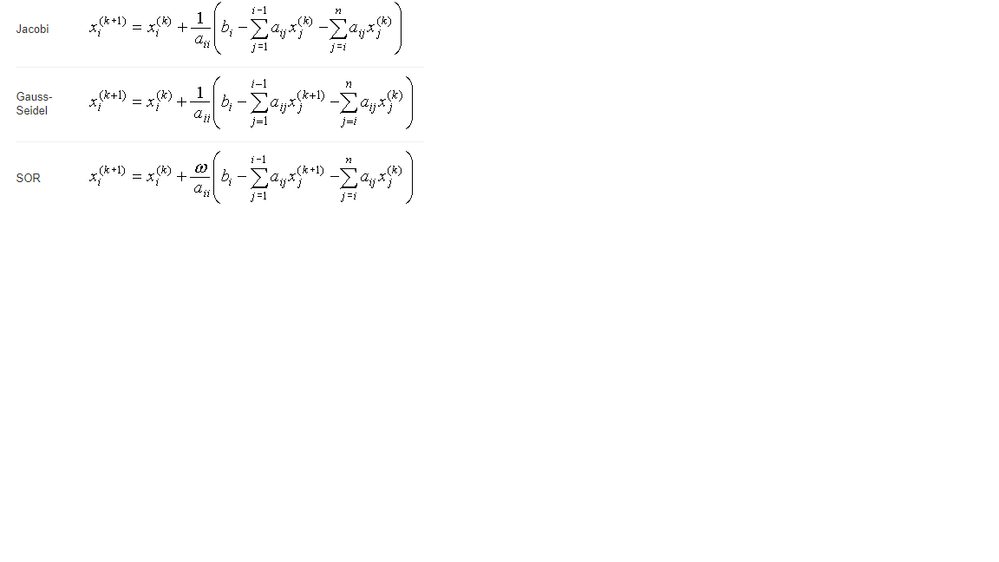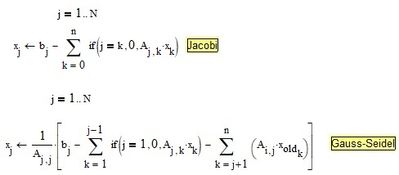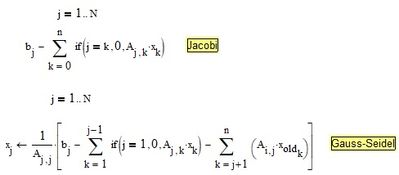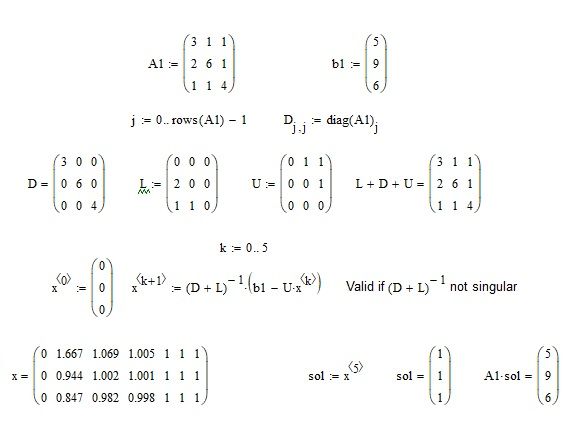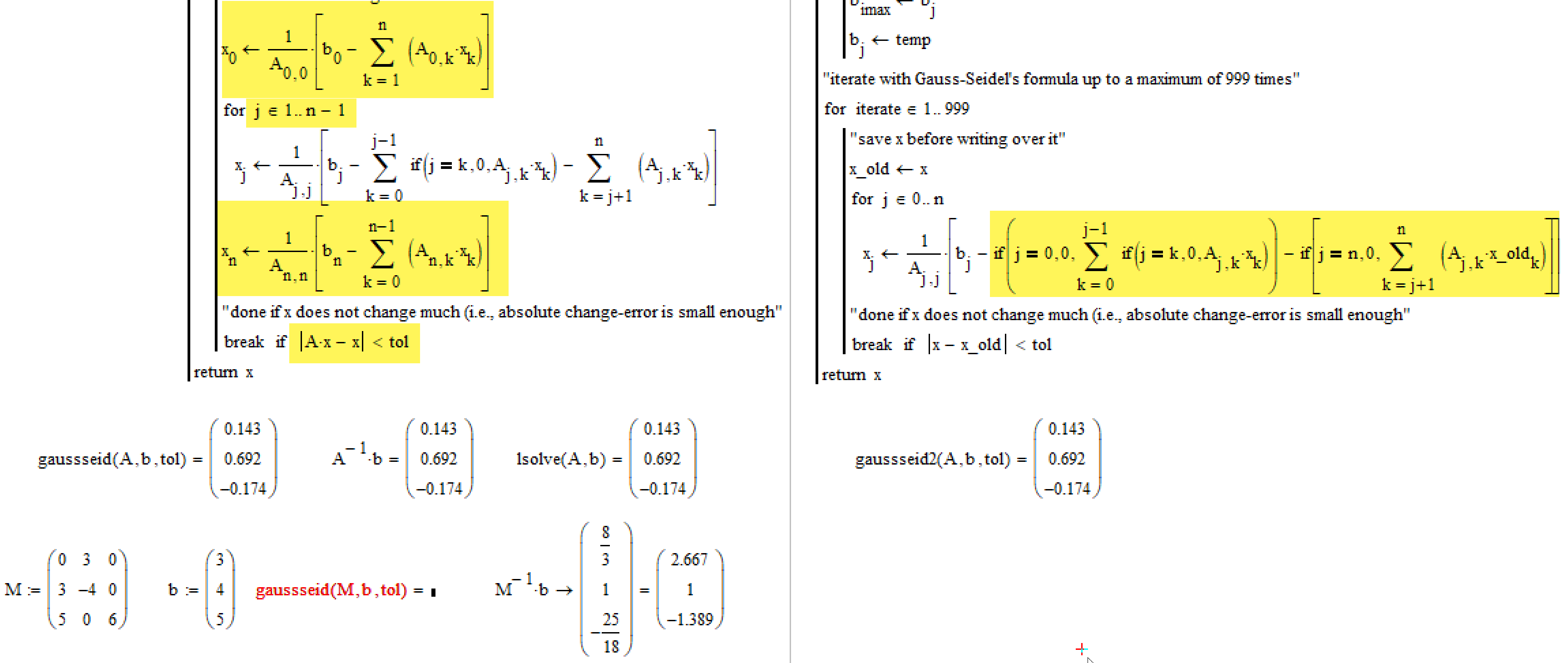Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Problem of construction of the Gauss-Seidel Mathcad Operator for the solution of a linear systems
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Problem of construction of the Gauss-Seidel Mathcad Operator for the solution of a linear systems
I cannot make to work the algorithm of the attached file containing Gauss-Seidel Operator for linear systems. Can someone give an advice, please? I attached it.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc's Mathcad 11 (which uses Maple for symbolics) can expand that expression, but Mathcad 15 (and 14) and also Prime use Mupad for symbolics and would refuse to display the result. Don't think that this is due to the symbolic engine but rather a design change in Mathcad itself. Somebody at Mathsoft probably thought that it would be a good idea not to let a symbolic result spread some pages widths - sorry guy, but it was not a good idea.
While MC13 still uses Maple (which is far superior over MuPad) it also had some severe deficits. Thats the reason many consider Mathcad11 as the best version ever. Alas, times go by and from todays point of view its probably MC15 to favor.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For starters:
- The keystroke for a range variable is a semicolon (;) not two periods (..) Mathcad will show two periods, but it won't understand them.
- "break" is a programming key word, it cannot be typed.
- If you want a literal subscript in a variable (in version 15) you type a decimal (x.old). An array subscript ([) will have Mathcad declaring an undefined variable.
- What is this?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, just on that expression is a problem. I wanted to write inside the Sum operator the below equation but it is impossible because appears automatically a void space before "if" that i dont understand why.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
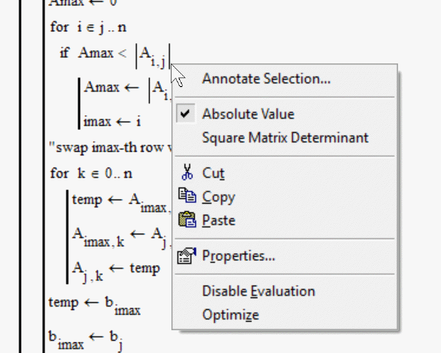
On point, additionally to what Fred had already said:
When taking the absolute value of a variable or an expression, Mathcad often can't know if you really mean the absolute value or if you want to take the determinant of a square matrix.
Rightclick at your absolute values and tell Mathcad what your intention is:
Concerning your confusion about the "if".
Mathcad offers two of them.
One is the programming if-statement which you chose via the programming palette or its keyboard short cut.
The second is the if-function,
The latter is what you want to use here. this time you simple type "if" and don't chose from the palette.
Nevertheless - when I correct all those errors, i ran into a divison by zero error. You may want to look over it again.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, typing directly the command "if" it is allowed the trick. But the issue remains unsolved as we still dont have the solution through Gauss-Seidel Method.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It looks like you are just retyping a program from a print of a Mathcad sheet.
So check your sheet for typos and keep in mind that there is a big difference between vector indices and literal indices (as you would use for x.old).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Found your typo:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
This is Jacobi's algorithm and not Gauss-Seidel's algorithm
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@-MFra- wrote:
Hi,
This is Jordan's algorithm and not Gauss-Seidel's algorithm
Dont thinks so.
Gauß-Jordan ist not an iteration algorithm which produces approximations but gives us exact results.
What we see in the listing is an iteration which yields approximations with a certain tolerance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, it has been a lapsus, not Jordan but Jacoby algorithm..................Jordan was a friend of mine........
Gauss-Jordan algorithm is :
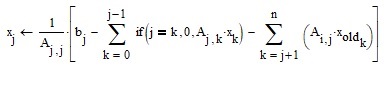
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Gauss-Jordan algorithm is :
? You mean Gauß-Seidel, don't you?
Otherwise you are perfectly right. Its not Gauß-Seidel what we see here, but its Jacobi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ok, I used the algorithm from "gauss-seidel-v7.pdf". The three methods that are appropriate are: Jacobi, Gaus-Seidel and Gaus-Seidel with Over-Relaxation (SOR). I also attached the file that I used. Thank you, I will insert the corrections and I will share again the corrected file in order to be used by others in the future.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sure I wanted to say Gauss-Seidel .... and the one implemented is by Jacobi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It cannot be the last term A_i,j * x_old_k. Maybe something like A_i,j * x_old_j or A_i,k * x_old_k or A_j,i * x_old_i.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For a range from (e.g.) 1 to 10 you type
1;10
and it shows as
1 .. 10
( if you type 1..10 you get 1..10 and an error message)
And you have an undefined variable named 'old'. Instead of x[old you probably need x.old. It does not show as a big difference, but Mathcad understands it completely differently:
While 'x.old' is a simple variable, the writing 'x[old' refers to an array 'x', specifically to its element with index 'old'
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good observation, I inserted ";" but still not results.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Its not only the ";"
The problems you have in your sheet were already all covered by Freds first answer yesterday! Look it up and read again.
1) ; instead of ..
2) x.old instead of x[old
3) don't type "break"
After you corrected those errors you will be facing and invalid matrix index error.
This is due to the fact, that Mathcad handles sums not according to the mathematical definition (which your pdf seems to rely on) but rather handles a sum like a programmed for-loop.
The Problem occurs in your sum where index k runs from 0 to j-1 and the first time the value of j is -1. In math its usually defined that this sum returns 0, but Mathcad will let it run down from 0 to -1. The error you encounter is because -1 is not a valid array index of course.
You will have to put some more time into your sheet as you will have to cope with that problem, as Mathcad will not return the so called "empty sum" (which is 0 by definition) when the upper limit in a sum is lower than the lower limit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
yes, 2 of the 3 statements are respected, but the instruction "break" cannot be excluded as it stops the running after the condition "<tol is satisfied.
Anyway, I'll do few more trying then I will renounce if no results.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You cannot type 'break', but have to choose it from the programming panel.
Success!|
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Of course, the Programming panel, that is always the first choosing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@tubar wrote:
yes, 2 of the 3 statements are respected, but the instruction "break" cannot be excluded as it stops the running after the condition "<tol is satisfied.
Fred (and me) did not mean that you should omit the break command. What we meant is that it doesn't work if you simply type in the word "break" as you have done.
But I see that you have already corrected that mistake, too, and now you are faced with the "invalid array index" error, as I had written before.
You may consider to let the outer loop run from j=1 to n-1 and deal with the cases j=0 and j=n separately.
Alternatively you could build a clumsy if-construction around the sum, which return 0 if the upper limit would be lower than the lower.
Anything wrong with A^-1 * b = (as seen in my first answer here) or with lsolve(A,b)= ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner,
nothing wrong with lsolve()
other than that it was never on my radar...![]()
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is not powerful just simply writing A^-1. For high count equations it cracks. That's why remain sustainable methods like Gauss-Seidel, Jacobi, Cholesky, etc.
In fact when you write A^-1, LucMeekes, behind the scene the software use one of the mentioned methods without to tell you how. A^-1 result is a BLACK BOX, it is not an interest for it now.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@tubar wrote:
It is not powerful just simply writing A^-1. For high count equations it cracks. That's why remain sustainable methods like Gauss-Seidel, Jacobi, Cholesky, etc.
In fact when you write A^-1, LucMeekes, behind the scene the software use one of the mentioned methods without to tell you how. A^-1 result is a BLACK BOX, it is not an interest for it now.
I'm sorry!
You're right, there are numerical calculation "black boxes" behind each of the Mathcad function calls. But they are tried and vetted processes that have been shown to be correct. (Yes, there are bugs as in all software; but there's also a team of people working to smash the bugs.)
If you're writing your program as a learning exercise, then fine, have at it.
If you're developing a tool to publish for your use (and our use), then PLEASE STOP!
Even once you get past the issues you have demonstrated learning the editor you will be hard pressed to create a tool that will be as robust as what we already have embedded in Mathcad.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ehh, I dont want to create a dilemma about finding the solutions of a linear system of equations. I just pursue Gauss-Seidel Method and not the direct inverse of a matrix like A^-1 . The use of A^-1 is qute useful for symbolic calculation.
At the moment I want to find a parallel comparison between a C++, a Matlab and a Mathcad Code.
Until now I found the codes in C++ and Matlab for Gauss-Seidel, and I want further to find the Mathcad one.
This is C++ for example:
#include<stdio.h>
#include<math.h>
#define X 2
main()
{
float x[X][X+1],a[X], ae, max,t,s,e;
int i,j,r,mxit;
for(i=0;i<X;i++) a[i]=0;
puts(" Eneter the elemrnts of augmented matrix rowwise\n");
for(i=0;i<X;i++)
{
for(j=0;j<X+1;j++)
{
scanf("%f",&x[i][j]);
}
}
printf(" Eneter the allowed error and maximum number of iteration: ");
scanf("%f%d",&ae,&mxit);
printf("Iteration\tx[1]\tx[2]\n");
for(r=1;r<=mxit;r++)
{
max=0;
for(i=0;i<X;i++)
{
s=0;
for(j=0;j<X;j++)
if(j!=i) s+=x[i][j]*a[j];
t=(x[i][X]-s)/x[i][i];
e=fabs(a[i]-t);
a[i]=t;
}
printf(" %5d\t",r);
for(i=0;i<X;i++)
printf(" %9.4f\t",a[i]);
printf("\n");
if(max<ae)
{
printf(" Converses in %3d iteration\n", r);
for(i=0;i<X;i++)
printf("a[%3d]=%7.4f\n", i+1,a[i]);
return 0;
}
}
}
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So much easier to understand.
Can you write it without the "#include<math.h"? Because this line just imported a whole bunch of "black boxes." And we don't like black boxes!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My mentioning of solving with the inverse coeff matrix or using solve was directed at Luc as he had asked if using Mathcads built-in methods would be an option.
You may be right about the inverse matrix being a problem with certain big unstable systems. lsolve or using a solve block usually will do the job pretty well. Sure Mathcad is using some of the established methods behind the curtains, but probably implemented more stable and robust and with better error checking than your self-made ones and also possibly quicker in execution.
I just thought you were trying to implement the various solving algorithms for studying purposes, not because you intend to use it for real.
Have you already changed the program to deal with the different implementation of the summation in Mathcad?
You will get the correct results, if you do. But there still ist something wrong with the way you manipulate the matrix A in the first part of your program. Try changing your matrix A so that there is a zero at the upper right instead of the 5 and you will see. Your rearranged matrix still has a zero in one of it diagonal elements!
As you can see on the left side of the pic, I got rid of x_old as its not really necessary. There sure are more elegant ways to implement Gauß-Seidel in Mathcad - I was just repairing working from what you had provided.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
OK, I will try several ways these days, but if will not work I will renounce. Thank you all for suggestions.