Skip to main content
M
M_U1-Visitor
1-Visitor
March 29, 2019
Question

Problem with FFT

  • March 29, 2019
  • 3 replies
  • 7244 views

Hello,

 

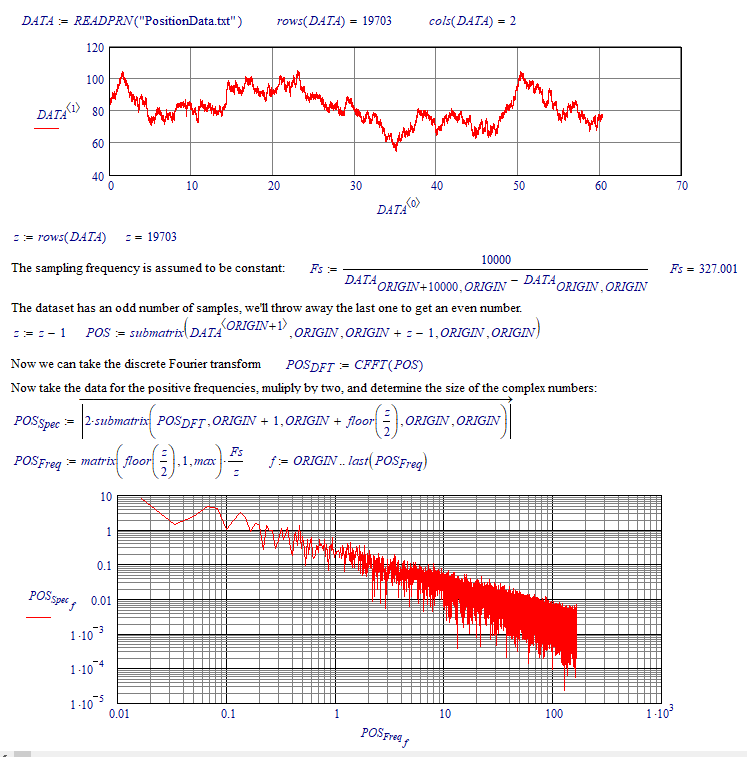
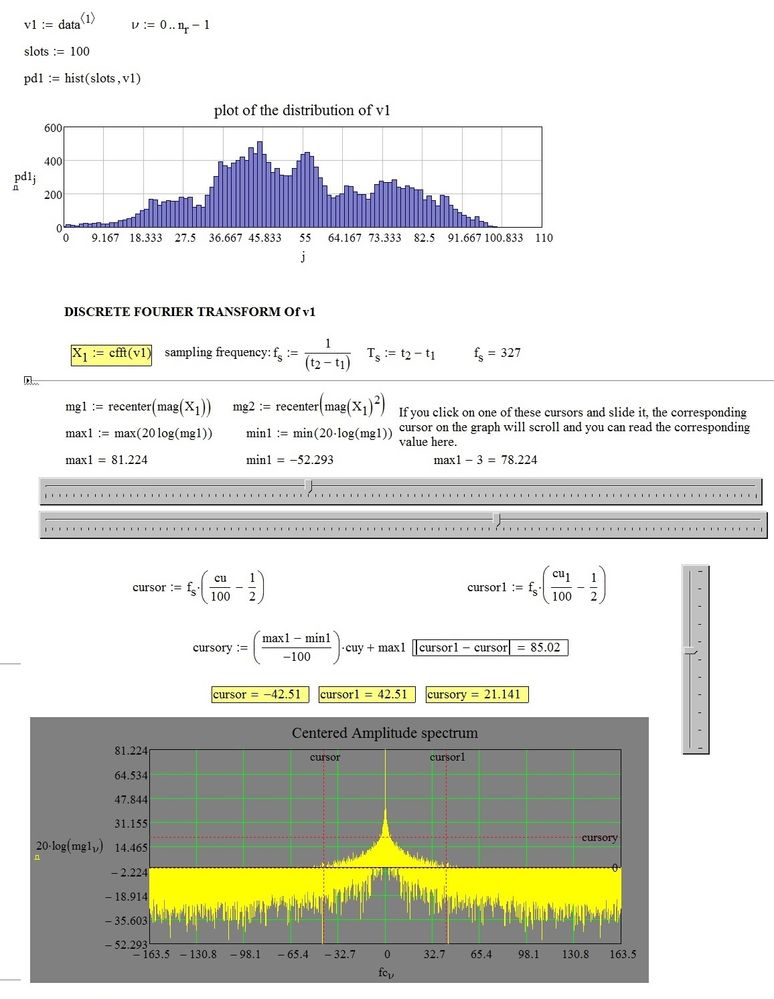
I have a data that contains the position of a particle as a function of time. When I apply the fourier transform I do not get any frequencies however through the time position graph and the position histogram, I can see that the particle has a position around which it oscillates. I also need to calculate the power spectral density (PSD) as a function of frequency. Has anyone ever worked with something like that?

The original data is attached.

 

Thnak you.

 

Ulisses

3 replies

L
LucMeekes23-Emerald IV
23-Emerald IV
March 29, 2019

Something like this...?

LM_20190329_FFT.png

Success!

Luc

F
Fred_Kohlhepp23-Emerald I
23-Emerald I
March 30, 2019

Unless I have forgotten, the first term in a CFFT is the steady value (equals the mean.)  The first frequency should then be zero,  And the magnitude (except for the first term) should be doubled.

 

L
LucMeekes23-Emerald IV
23-Emerald IV
March 30, 2019
I took off the first element, kept the remainder of the first half of the spectrum data and doubled that.
    -
    -MFra-21-Topaz II
    21-Topaz II
    March 30, 2019

    Hi,

    This is all I can do with the data I have:

    for U_M.jpg

    for U_M 1.jpg

    -
    -MFra-21-Topaz II
    21-Topaz II
    April 2, 2019

    for U. M. 01.jpgfor U. M. 02.jpgfor U. M. 03.jpgfor U. M. 04.jpgfor U. M. 05.jpgfor U. M. 06.jpg

    M
    M_U1-VisitorAuthor
    1-Visitor
    April 5, 2019

    MF,

    sorry for the delay of the answer because I was reading about it. 

    You suggested even more than I needed. I am still analyzing the details of your suggestion.

    Thank you

    L
    LouP12-Amethyst
    12-Amethyst
    April 1, 2019

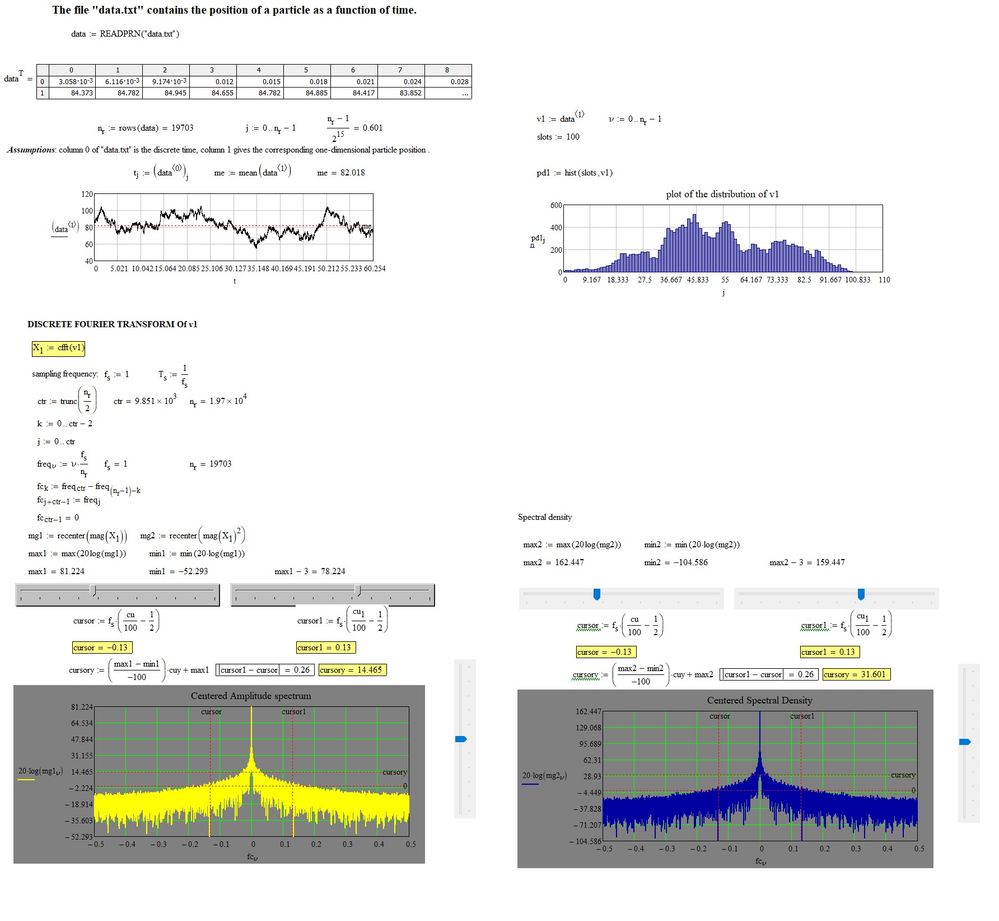
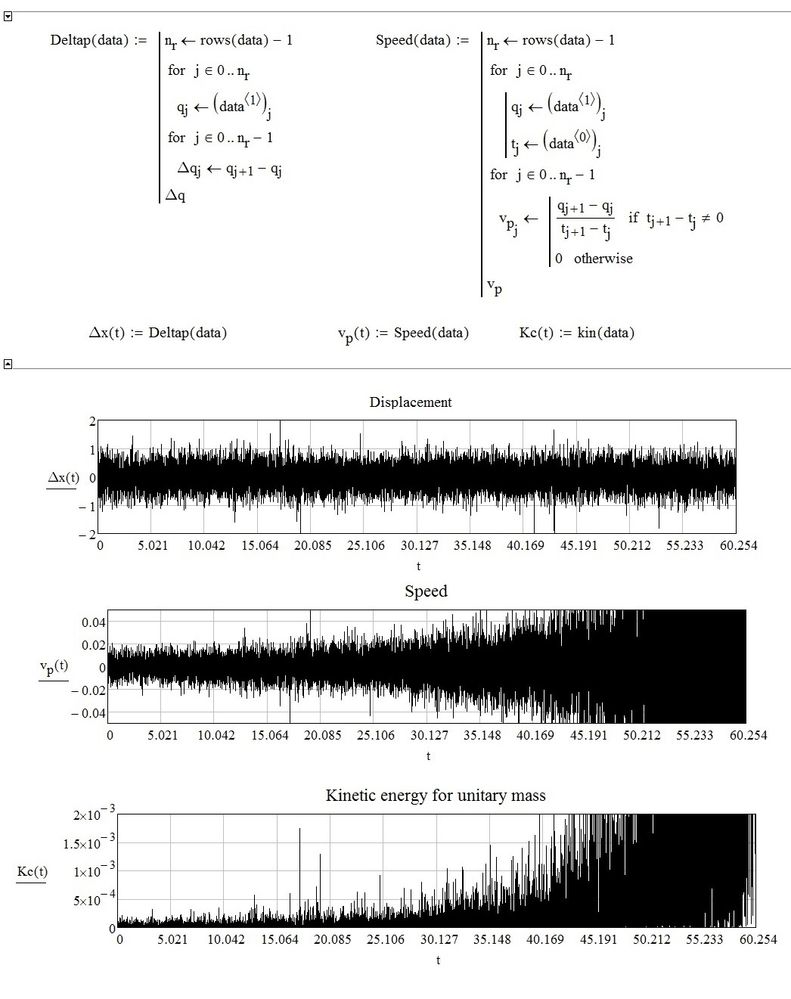
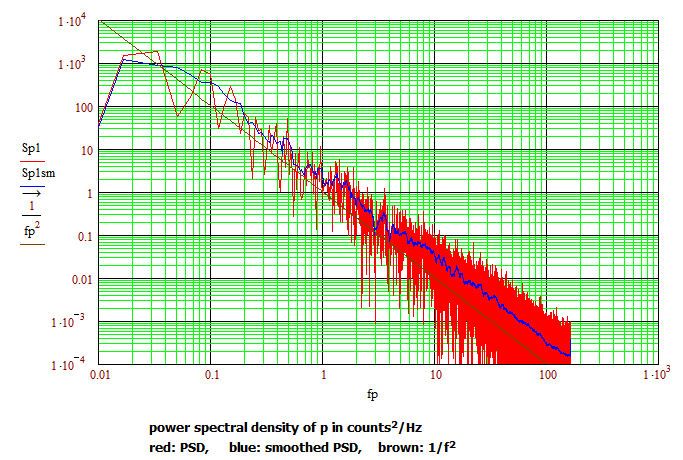
    The particle does move back and forth about its average value (~82). However, it does so essentially randomly, with no single discernible frequency. Luc has done the essential calculation. However, there is a scale factor that needs to be applied in order to get the correct quantitative values for the power spectral density (PSD). For the signal p(t) with N samples, let P = CFFT(p). Sp1, the single sided PSD is defined for f=0 to fNyquist, and is given by

    sp_formula.jpg

    The factor of 2 sums the power for both positive and negative frequency components for f>0. Since all of the DFT routines, including CFFT, deal just with the data vectors, there is no information about the horizontal scale, be it time, distance, or something else. The N/fs factor provides the correct scaling (with CFFT) so that the result can be interpreted as a power spectral density. If the units of the data p are mm, then the PSD will have units of mm^2/Hz.

    The plot shows my calc of PSD, a smoothed version, and a reference line of 1/f^2. The PSD follows the 1/f^2 behavior quite closely over the full frequency range. MCD v11 file and pdf attached.

     

    Lou

    DFTcalc.jpg

     

      M
      M_U1-VisitorAuthor
      1-Visitor
      April 5, 2019

      Loup,

       

      sorry for the delay to answer because I was studying the subject. I think that's exactly what I needed. I'm analyzing the same data in KaleidaGraph and find something very close. I have a doubt, 

      the term 

       

      should converge to some specific value?

       

      Thank you

       

       

       

       

       

       

      L
      LouP12-Amethyst
      12-Amethyst
      April 6, 2019

      I don't see any anything in the attachment. Is it an image? Please try again.

       

      Lou

      Terms & ConditionsCookie settingsAccessibility statement