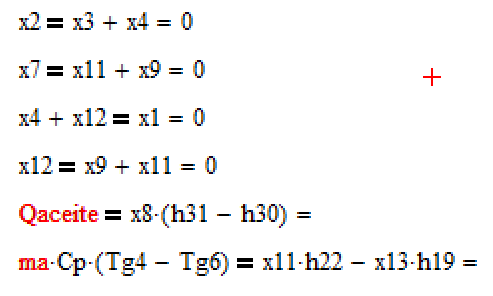Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Problem with given/find in linear system. "This variable is undefined"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Problem with given/find in linear system. "This variable is undefined"
Hello,
I am doing this exercise about a combined cycle where some of the enthalpies are known.
The problem is when i try to solve the system the error "This variable is undefined" constantly appears.
I have tried both of the systems i know about describing the solution:
Solution:=Find(x1,...) and (x)
(y) :=Find(x1,...)
Hope there is solution.
Thanks in advance.
IG88
(Uploaded the .xmcd)
- Labels:
-
Mechanical_Engineering
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You did not set all the initial conditions.
- Tags:
- .
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, you are completely right. I forgot to copy those variables. Thanks @VladimirN
It shows me the same error with Find and i have tried to use Minerr but shows nonsense results, knowing the differences between them, so i will continue finding a solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry!
Better to use the lsolve function for this problem! Not given-find!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think I have to disagree with you, Valery.
Using lsolve you are forced to structure your problem nicely. The advantag of a solve block is that you can make a mess of the problem.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The main problem i have just realised is that in some of the equations some unknown variables are multiplying each other, such as x8 and h31. I thought that the idea of using lsolve was great until i realised about that.
I would change the equations and assign values for the h24, h31 and h32 so there isn´t any variable multiplying another.
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Check please your equation with = and see an error!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
i think that it is before i copy those variables. I forgot to upload the new .xmcd.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
M*x=v
M:=[] v:=[]
cols(M)=n1
rank(M)=n2 rank(augment(M, v))=n3
n1=n2=n3!!!
x:=lsolve(M, v)=
M*x-v=
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is that how to solve this system with lsolve?
I have seen something equal to that method dividing the matrix in 4 and then using:
M = stack(augment(M00,M01),augment(M10,M11))
The problem is that there are some variables that multiply other (x8*h31), making a non linear system, or am i wrong?
That makes impossible using matrices using a column for each variable.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Non linear.