Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Question about using pdesolve in second-order derviative
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Question about using pdesolve in second-order derviative
Hi everyone,
I met a question, when I use "pdesolve" in mathcad. The failure is listed in the picture as following:

It told me that the second-order are not allowed, but I have another successful example from the website, which can be seen in the following picture:
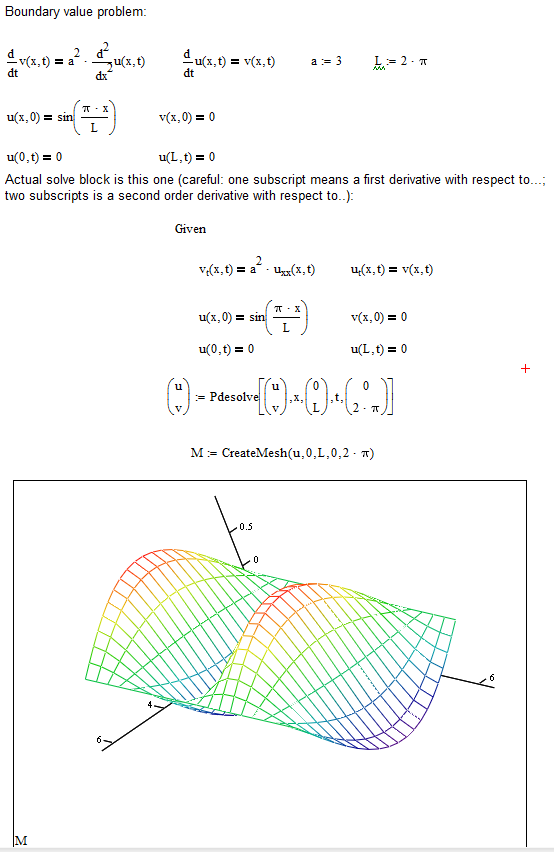
In the above successful case, we can see it also contains uxx(x,t), which is second-order derivative.
Anyone can help me about my failure in my case? I attach my input file in the annex, please kindly find it.
Best wishes,
Jason
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Jason,
your differential equation problem is somewhat weird.
First off: you have two differential equations, one entirely in terms of the function a(x,t) and its (partial) derivatives, the other entirely in terms of the function T(x,t) and its (partial) derivatives. This leads me to think that you can solve a() and T() separately.
Then observe that the two differential equations are the same, except for some constants: alpha instead of D, and kappa versus kappa multiplied with and divided by some constants. This would mean that the two functions a() and T() will (probably) be the same except for some constants.
Now for a() you have 4 boundary conditions, but for T() you only have 3. Either 4 is too much for a(), or 3 is too few for T(), or they're both off.
I experimented a bit to see if I could solve the problem symbolically. Here's the result:





Unfortunately the values of a0, a1 and b0 cannot be solved in terms of the defined variables,
using the boundary conditions:

(from the 3rd equation, either b0 or a1 must be 0.
If b0=0, then the fourth will also hold, but the first two equations will not hold.
If a1=0, then the fourth can only hold when also b0=0...
The LHS's of the first two equations are equal, but the RHS's aren't, 1=1/2?)
Are you sure the problem is well formulated?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much to anyone, who can solve my problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
May be figs 18.10-18-12
here Study 18. Differential Equations in Thermal Engineering
help you.
I use not pdesolve but programming Method Finite Elements
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The example from the website does use a second derivative, but in x, not in time.
In your case a second time-derivative of both functions is involved:

Not allowing a second time-derivative is an undocumented limitation. It's not in the list of error-messages and the limitations do say:
"For a PDE, there must be an initial condition u(x,0), and n boundary conditions, where n is the order of the PDE, for each unknown function. Boundary conditions can be either Dirichlet (u(x0,t) = f(t)) or Neumann (ux(x0,t)=g(t)), and can be specified at either endpoint of the spatial integration range.
In each case, the endpoints used in boundary conditions must match the endpoints specified in the ode/pdesolve command.
"
Your number of boundaries (7) is rather high.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
Thank you for your detail explanation. ![]() Can you tell me what should I do to solve this problem? I have known the reason; however, I still don't know how to deal with it.
Can you tell me what should I do to solve this problem? I have known the reason; however, I still don't know how to deal with it.
Best wishes.
Jason
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Jason,
your differential equation problem is somewhat weird.
First off: you have two differential equations, one entirely in terms of the function a(x,t) and its (partial) derivatives, the other entirely in terms of the function T(x,t) and its (partial) derivatives. This leads me to think that you can solve a() and T() separately.
Then observe that the two differential equations are the same, except for some constants: alpha instead of D, and kappa versus kappa multiplied with and divided by some constants. This would mean that the two functions a() and T() will (probably) be the same except for some constants.
Now for a() you have 4 boundary conditions, but for T() you only have 3. Either 4 is too much for a(), or 3 is too few for T(), or they're both off.
I experimented a bit to see if I could solve the problem symbolically. Here's the result:





Unfortunately the values of a0, a1 and b0 cannot be solved in terms of the defined variables,
using the boundary conditions:

(from the 3rd equation, either b0 or a1 must be 0.
If b0=0, then the fourth will also hold, but the first two equations will not hold.
If a1=0, then the fourth can only hold when also b0=0...
The LHS's of the first two equations are equal, but the RHS's aren't, 1=1/2?)
Are you sure the problem is well formulated?
Luc





