Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Question
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Question
Hy! I've created an algorithm. I've attached it.
In this algorithm I have assigned initial values to x1,y1,p1,p2,p3,p4.
Then I inserted a "while" function. My question is: why don't the variables take the new values?
For example: Q is the new value of A. This means that x1,x2,p1,p2,p4 have new values, but the results that the algorithm gives me are still the initial values. I want the new values that variables have untill the "while" function is fulfilled.
Thanks.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess the iteration should be sligthly different, but the main problem seems to be that the initial value for x1 and y1 are chosen in a way, that the RHS of the inequality would already yield a result greater than N if p1,p2 and p2 would be calculated the same way as shown in the iteration loop. So the iteration runs exatly one step and stops when that RHS is approx 10.7...
Solution could be to chose larger initial values for x1 and y1.
Find attached a routine which outputs a table so you can watch the values change. You will have to find suitable start values for x1 and y1.
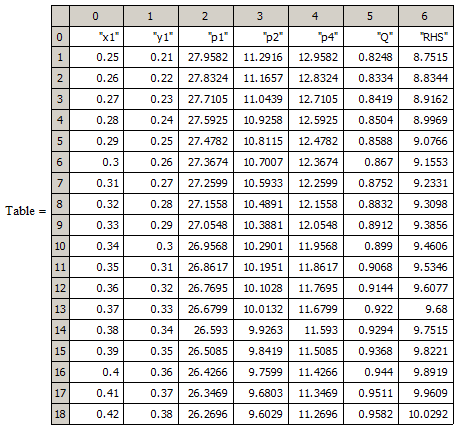
But is it really mandatory that both x1 and y1 are changed the same way (-0.01)? I guess you are simply trying to search for values x1 and y1 which makes the RHS equal to N.
If thats true, so why not try a solve block:
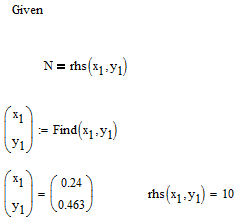
Thats only one of an infinite number of solution pairs, so you could add some appropriate constraints like
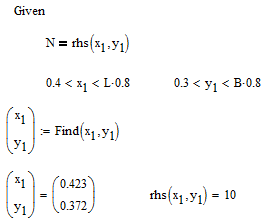
or
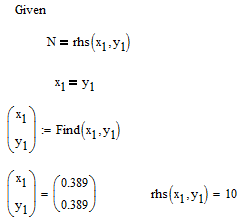
Basically your RHS represents a surface in 3D which you have to intersect with the plane at height N:
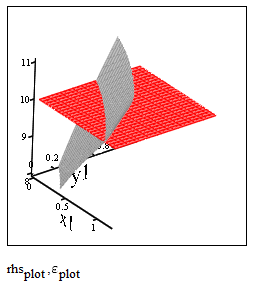
The curve of intersection can also be drawn as a 2D plot, y1 over x1:
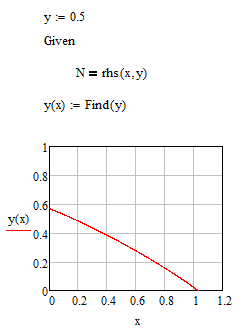
BTW, John Smith, isn't this question related to this one of John Air: http://communities.ptc.com/message/240228#240228 ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
John Smith wrote:
...My question is: why don't the variables take the new values?
Because the initial value of that long expression is less than N. Hence the while loop is never entered!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I know. But the while loop makes the value grow until that N>... is not fulfilled.
Any idea of how can the while loop be entered?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The while loop is entered only once. The values of a, b, c, d, e are assigned the starting values of x1, y1, p1, p2, p4. Then the values of x1, y1, p1, p2, p4 are changed. The while loop is not entered a second time, so what you get are the starting guesses. If the values of a, b, c, d, e are assigned after you have assigned the values for x1, y1, p1, p2, p4 you will see the values for the last time it entered the loop, rather then the one before that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I tried your proposal and noticed a significant change.
The values are still not the ones that I want. I will review it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Why are they not the ones you want? They are the first set of values that makes the expression greater than N.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
x and y have an initial value each. In the while loop they get smaller a-0.01 and b-0.01. That means that p1,p2 and p4 are getting bigger. (Q is getting smaller and the value N/Q is getting bigger). But my x and y values are going negative.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
John Smith wrote:
In the while loop they get smaller a-0.01 and b-0.01.
...
Q is getting smaller
Are you sure?
While a and b sure decrease, L-a and B-b will increase.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes. But Q is an area. It's getting smaller.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well, if all you do is move the defintions around as I described, you will get weird results. Q is defined in terms of a and b, as are the new values of x1 and y1. But if you move the definitions of a and b down, then for those defitions of Q, x1, and y1 a and b are not defined. So you need to make a couple of other adjustments to accommodate the new assignment order. Does this do what you want?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess the iteration should be sligthly different, but the main problem seems to be that the initial value for x1 and y1 are chosen in a way, that the RHS of the inequality would already yield a result greater than N if p1,p2 and p2 would be calculated the same way as shown in the iteration loop. So the iteration runs exatly one step and stops when that RHS is approx 10.7...
Solution could be to chose larger initial values for x1 and y1.
Find attached a routine which outputs a table so you can watch the values change. You will have to find suitable start values for x1 and y1.

But is it really mandatory that both x1 and y1 are changed the same way (-0.01)? I guess you are simply trying to search for values x1 and y1 which makes the RHS equal to N.
If thats true, so why not try a solve block:
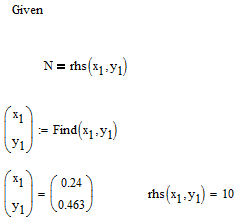
Thats only one of an infinite number of solution pairs, so you could add some appropriate constraints like
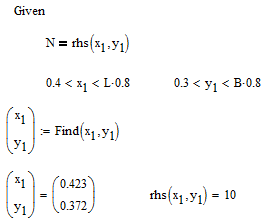
or
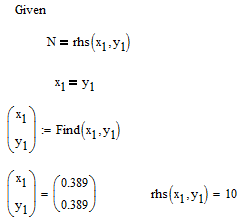
Basically your RHS represents a surface in 3D which you have to intersect with the plane at height N:

The curve of intersection can also be drawn as a 2D plot, y1 over x1:

BTW, John Smith, isn't this question related to this one of John Air: http://communities.ptc.com/message/240228#240228 ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
BTW, John Smith, isn't this question related to this one of John Air:
Good catch!
Funny how the answer doesn't change, even when the questioners name does ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Funny how the answer doesn't change,
nor did the subject ![]()





