Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
RQ factorization using QR
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
RQ factorization using QR
Has anyone done RQ factorization using the QR matrix function?
I understand that this can be done using "row reversal" but I'm not sure how to proceed.
Solved! Go to Solution.
- Labels:
-
Other
- Tags:
- factorization
- matrix
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Alvaro,
Unfortunately your soultion doesn't perform "RQ" factorisation as it is generally defined.
As you observe, it provides a factorisation into a Lower Triangle and Orthoganal matrix pair.
Anyway, I have now figured out how to do this and I have attached my solution to this post.
Best Regards
John
For the benefit of others:
Recall that "QR factorisation" decomposes a matrix A into an othogonal matrix Q and an upper triangular matrix R such that A=Q.R
"RQ" factorisation decomposes a matrix B into a upper right triangle matrix, say T and an orthogonal matrix Z such that B=T.Z
Note the difference in order of multiplication for the two matrix types (triangular and orthogonal)
Actually, the situation would be more clear if we renamed "RQ factorisation" as "TZ factorisation" then there would be less confusion between the two decompositions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Like this?

Try and play with it by modifying M (not only its values, but also its size and shape.)
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
Thanks for responding. I appreciate your effort but this doesn't quite answer my question. I am able to do QR factorisation using the Mathcad function provided but I need to do RQ factorisation, which is a slightly different factorisation that gives different ‘Q’ and ‘R’.
As you demonstrated, “QR factorisation” of a matrix A gives two matrices, say B and C, such that A=BC where B is an orthogonal matrix and C is upper triangular.
But “RQ factorisation” of a matrix A gives two matrices, say D and E such that A=DE where D is upper-triangular and E is orthogonal.
Matrices B,C,D and E are generally all different.
Anyway, I think I nearly have this sorted now - I hope to post the answer soon, in case anyone is interested.
Cheers
John
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi John. Hope this helps. But not very sure if you need to reverse R (or eventually Q too) because my R is lower triangular. There are some few variants for this algorithm. But what actually is important, is that:
- QR is Gram-Schmidt orthoganilization of columns of A, started from the first.
- RQ is Gram-Schmidt orthoganilization of rows of A, started from the last.
Also in my example, Q'*Q = Q*Q' = identity, and I know that for Q'*Q this is not always desiderable. Finally, notice that I use Origin = 1.
Best regards.
Alvaro.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Alvaro,
Unfortunately your soultion doesn't perform "RQ" factorisation as it is generally defined.
As you observe, it provides a factorisation into a Lower Triangle and Orthoganal matrix pair.
Anyway, I have now figured out how to do this and I have attached my solution to this post.
Best Regards
John
For the benefit of others:
Recall that "QR factorisation" decomposes a matrix A into an othogonal matrix Q and an upper triangular matrix R such that A=Q.R
"RQ" factorisation decomposes a matrix B into a upper right triangle matrix, say T and an orthogonal matrix Z such that B=T.Z
Note the difference in order of multiplication for the two matrix types (triangular and orthogonal)
Actually, the situation would be more clear if we renamed "RQ factorisation" as "TZ factorisation" then there would be less confusion between the two decompositions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Neat.
Could you please mark your own answer as correct. It will help others find the solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks. Done.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi John. There are some variants of the procedure. As I say before, some ones are obtained reverting the matrices. Benefits of that? In that cases (not sure if always, but is my best guess) det(Q) = 1, (not -1, like with your procedure). That implies that Q is good for movements which preserves the order of the transformed points (that is called as a "special orthogonal case"). Above is how can get an R upper triangular, and Q with det(Q) = 1, with reverting the order in the previous post.
Best regards.
Alvaro.
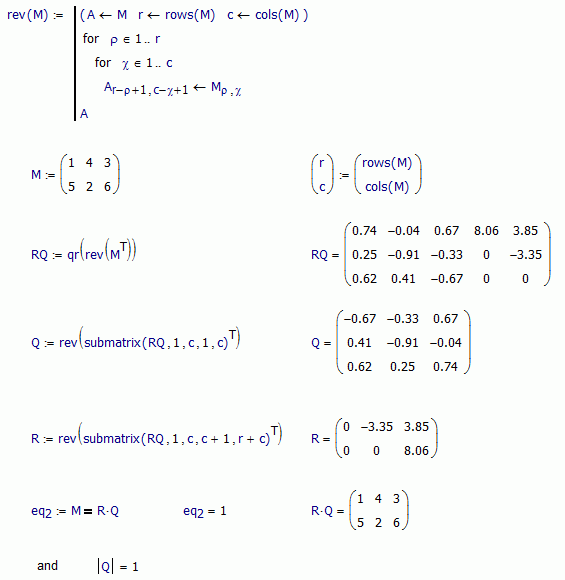
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Alvaro,
Thanks again for responding.
You clearly know more about this subject than me (it is way off my field) so I'm sure your argument is correct about the benefit of having det(Q)=1
In my application I need R so it doesn't matter about det(Q), but your solution is also tidier than mine - it is what I was originally trying to find - so thanks again.
Best regards
John





