Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Real and positive root needed
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Real and positive root needed
How can I gat a Real and positive root - see the picture and attach (Mathcad 15 and, pardon, Mathcad Prime 2.0)

Solved! Go to Solution.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov schrieb:
Valery Ochkov wrote:
I will try to solve this task tomorrow with Maple.
Sorry, no sollution in Maple too
I let that Mathcad sheet run overnight and was presented with a "Out of Memory" error in Mathcad this morning.
I am surprised that Maple could not solve it, as you wrote. I assume you used stand alone maple or did you use Mathcad 11?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Valery Ochkov schrieb:
Valery Ochkov wrote:
I will try to solve this task tomorrow with Maple.
Sorry, no sollution in Maple too
I let that Mathcad sheet run overnight and was presented with a "Out of Memory" error in Mathcad this morning.
I am surprised that Maple could not solve it, as you wrote. I assume you used stand alone maple or did you use Mathcad 11?
Maple 15.
Not only me but a lot of people on Russian Maple forum cannot solve this problem (semisphere+cone).
A Simple cone - no problem:

A a semisphere+cone with numerical math of Mathcad 15 - no problem:
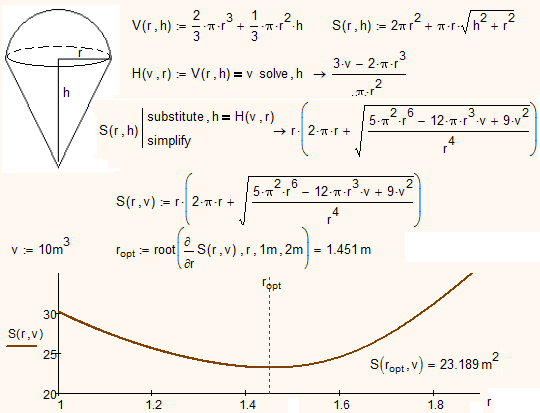
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not only me but a lot of people on Russian Maple forum cannot solve this problem (semisphere+cone).
So as far only Derive6 was able to do the job!? Great!
Anybody gave it a try with Mathematica?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Not only me but a lot of people on Russian Maple forum cannot solve this problem (semisphere+cone).
So as far only Derive 6 was able to do the job!? Great!
Show please!
Sorry, I think Maple's symbolic Math is more powerful than same one in Mathematica or Derive.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad is fine!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov schrieb:
Mathcad is fine!
???????
Right answer to every question 😉
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov schrieb:
So as far only Derive 6 was able to do the job!? Great!
Show please!
Seemes you overlooked it - I showed the Mathcad transcript of the Derive solutions in the attachment of that post
http://communities.ptc.com/message/196835#196835
The Derive file is gone as it never was saved.
Attachment is here http://communities.ptc.com/servlet/JiveServlet/download/196835-47557/Cone_Semisphere.xmcdz.zip
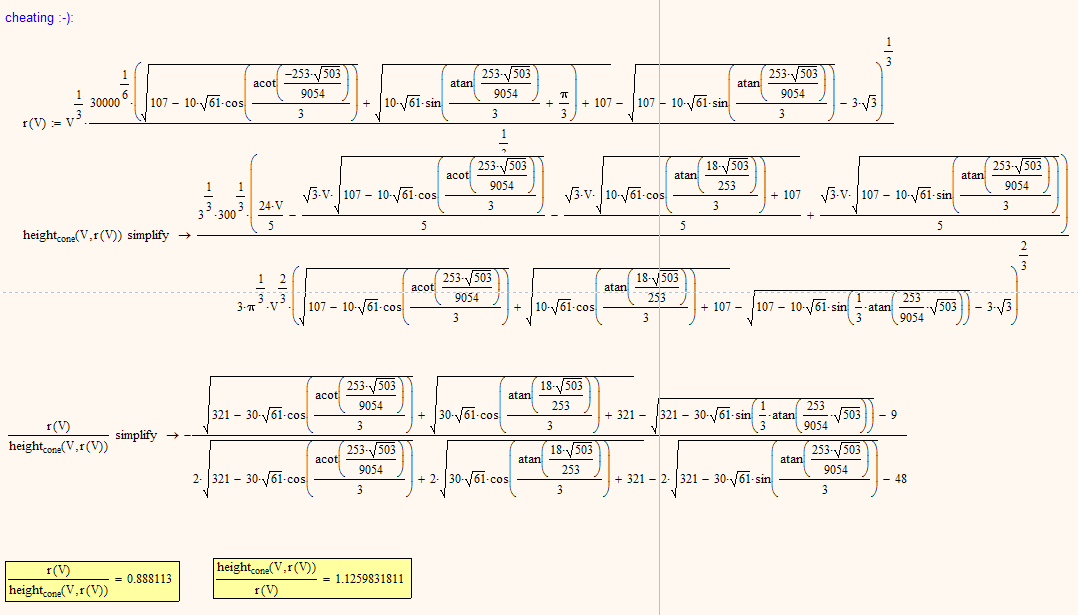
I've recreated the sheet. Find attached a pdf of it. Derive has a command switch to solve fo real solutions only, but in this case it failed. So we see 14 complex and 4 real solutions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the solution of the 12 elements and all are complex.![]()
In the second case(ConeEngHand.mcdx.zip), you had to manually select the solution. You can not do it automatically.See GIF file.
I am a beginner at Mathematica maybe there is a possibility of this solution. You may need to put on the Mathematica forum to consult.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the solution of the 12 elements and all are complex.

Strange, as there have to be 4 real and 14 complex solutions according to my DERIVE output and as one of the real solutions perfectly matches the numeric solution I tend to believe that Derive is right (at least with that one real solution). I only gave your pdf a quick look but oviously there has either to be a typo somewhere or the solution is OK and will simply to some real values for a positive, real value of V. Have you tried to set V=1 and see what happens, probably numerically approximate to get a better view.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For V = 1 the result is
r == 0.673485 - 6.28172*10^-17 i
increasing the accuracy to 30 the number after the decimal result is the:See attach GiF file
The equation for the assumed conditions, V> 0 and R> 0 gave me complex solution see: Sol2.7z zip file.
In Derive 6 result see another gif file.
Mathcad 15 and Prime Su..cks![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So with Derive you get the four real solution. I have to check why the modifier "real" did not work for me.
I would not say that Mathcad 15 (won't comment on Prime now) suc*ks (funny didn't know we have censorship here) but we know for a very long time that the symbolics in Mathcad are rather weak and it get worse witch the change from Maple to MuPad. But on the other hand not so weak that I wouldn't use it for everey day tasks, enjoying all the benefits I get from using Mathcad in contrary to other tools. As I already wrote Mathcad seems not to be the tool to use for really difficult and heavy symbolics tasks, buts it legit to give it a try anyway. Sidenote: Also when it comes to number theory, integer arithmetic, etc. Mathcad very soon has to give up. For that kind of tasks Derive sure is a good choice, too.
I always thought that Mathematica would be the tool to choose as THE reference in symbolics math. From what I see here - should I have been wrong with that?
At least I am very happy to seen how good Derive is doing an these jobs.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
So with Derive you get the four real solution.
Sorry, I see only two one:
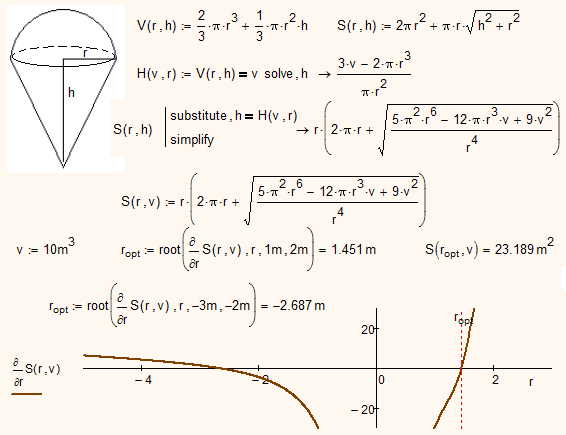
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
After numerical calculation and rejecting the imaginary part of the result is the same as in the Derive6.![]() see gif file.
see gif file.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
...and how many real roots?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
All 12 roots contain the imaginary part. This is the result of Mathematica. Assuming v> 0, y> 0, there is only one result, and also contains an imaginary part. If you take the real part of the result is correct.I'm a little confused why the results reported Mathematica.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This problem has a practical application - the production of ice cream with minimal wrapper:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
This problem has a practical application - the production of ice cream with minimal wrapper:
Thanks again for your solutions in Mathcad, Maple, Mathematica (no Matlab ![]() ) but...
) but...
Sorry, the problem of a semisphere & a cone was a not correct problem.
The correct problem is a problem of a part of sphere (a spherical cap) & a cone: ![]()
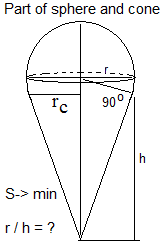
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So once again the problem has been changed.
For the problem with a part of sphere (not hemisphere), you need to specify the angle formed by the sphere radius and the vertical axis. Otherwise, minimization of the total area should eliminate the cone. In that case, h/r = 0 and the full sphere will be left. The angle of interest will be zero in that case.
I suppose you might want the answer as a function of that angle?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Harvey Hensley wrote:
So once again the problem has been changed.
For the problem with a part of sphere (not hemisphere), you need to specify the angle formed by the sphere radius and the vertical axis. Otherwise, minimization of the total area should eliminate the cone. In that case, h/r = 0 and the full sphere will be left. The angle of interest will be zero in that case.
I suppose you might want the answer as a function of that angle?
Bravo, Harvey!
I show this problem to my students.
90% go to Mathcad, Maple, Mathematica
10% go to... brain.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm, who would have expected that confusion arising out of that simple looking (on first sight) problem?
Am I correct in racapitulating as follows? (assuming none of us has made a typo or anything similar):
We are looking for a symbolic solution to an equation. From looking at the graph and/or numerical evaluation (assuming V is positive real) we know that we have to expect two real solutions - one negative, one positive (which we are looking for).
The results are:
- Mathcad: No symbolic solution found
- Maple: No symbolic solution found
- Mathematica9: 12 symbolic solutions found. All of them are complex, but some are "near" the two expected real solutions (if one ignores the imaginary part)
- Derive6: 18 symbolic solutions found, 4 of them real and the two, which we expected, are amongst them
I really would call that a puzzle!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But the best solution is from Mathcad - a complex of symbolic and numeric math:
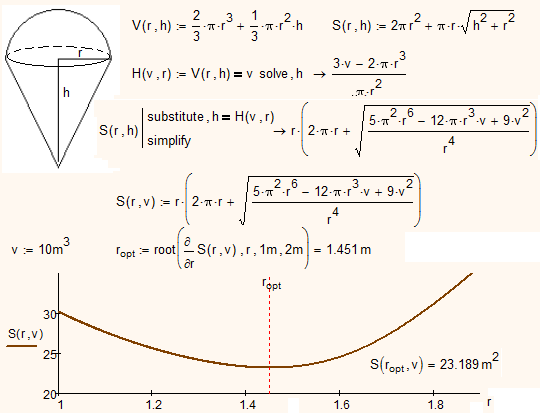
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov schrieb:
But the best solution is from Mathcad - a complex of symbolic and numeric math:
No, I disagree.
One has to admit that Mathcad simply fails when asked for a symbolic solution (as was demanded for in first place), while other programs don't.
A numeric or mix of symbolic and numeric solution could be achieved by all of the aforementioned programs.
Maybe it shows that PTC would be well advised to consider a change of the symbolic engine.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Reformulate the problem to find the ratio, not r. See attached and the figure below.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Harvey!
For a cone - no problem. A problem is/was for a cone and a semisphere or cone and a part of sphere:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery,
Is the problem to minimize the surface to volume ratio of the hemisphere+cone? If that is the case, then the answer is for the h/r ratio to be 0. The sphere has less area/vol than the conical shape.
In your numerical example, you have specified the volume. In my attached worksheet I have given an example with h specified. Note that the plot of the surface/vol ratio increases with h.r = h/r. Also note that the derivative of the surface/vol rate never goes to zero. Thus, the symbolic solve can't find a solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Harvey Hensley schrieb:
Valery,
Is the problem to minimize the surface to volume ratio of the hemisphere+cone? If that is the case, then the answer is for the h/r ratio to be 0. The sphere has less area/vol than the conical shape.
A complete sphere - yes, but If you reduce h/r to zero, you get a semispehere. You have to remember that the circular disk the cone is reduced to, adds to the surface, too, without contributing to the volume.
If you look for the ratio Surface to Volume you would have to compensate for the different units. You cannot express that ratio in h.r alone. You are either left with a single r (as in my attached file) or a h (as in yours) in the denominator. BTW, use the modifier "assume,ALL>0" to get a better simplification. So the limit for your ratio S/V for h.r against infinity is 3/h (in your example 30).
Because of the difference in units/dimensions minimizing S/V is different from asking for the ratio h/r for a given Volume.
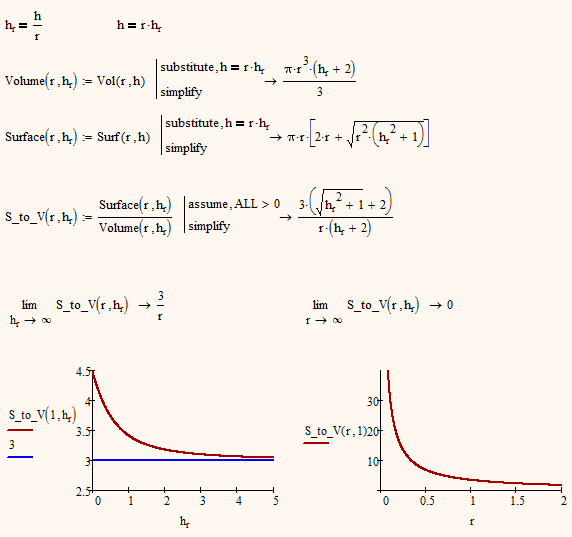
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner,
You are right. So I have a new worksheet attached. It shows the minimum in the S/V ratio at h/r > 0. It also shows via plots that the minimum is independent of the volume. This indicates that a numerical solution is adequate. Notice that the answer appears to be an irrational number. Do you think that is the reason that the solver can't find a symbolic solution?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This indicates that a numerical solution is adequate.
Sure it is. The discussion about a symbolic solution was more of academic interest anyway and to see, where the limits of Mathcad's symbolics are or if there are any tricks (like the substitutions) to get Mathcad solve the problem in a symbolic way.
Notice that the answer appears to be an irrational number. Do you think that is the reason that the solver can't find a symbolic solution?
No, that would be even worse than it is. Irrational numbers are exactly the reason why one might want to see an exact symbolic solution. You had posted a WS yourself where the symbolic result was sqrt(2), an irrational number. The exact symbolic solution to this problem is far more complicated, though. It was given by me in one of the worksheets I have posted (I think its in the last one, too) and was taken from the Derive solution. It simplifies to the numerical value derived by Mathcad so I assume its OK.
But we know that the symbolics in Mathcad can't compare to high end products like Mathematica. What was interesting to see was that a low cost product like DERIVE did better and that Maple as a high end competitor to Mathematica had to give up on that (only at first sight) simple task.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thats the wrong problem, Harvey.
This thread is going quite long with some subthreads and is rather difficult to follow now. I am getting confused myself, as with many other threads (sorry - discusisions!) which grow over the time, split and are going nonlinear.
Its ridiculous that PTC is not able to implement some simple standard viewing helps like the ability to collaps threads and subthreads, header view, look at the general structure of a thread (tree view), etc. I'd rather dispense with the ability of making friens, the like button, the silly points you get for posting, the blogs, photo, video and the document section (the latter could be useful, but as is now its so cluttered and unstructured so that its not useful at all), ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Thats the wrong problem, Harvey.
What problem is wrong?






