However, does it mean that the position of the solution on the graph and
Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Resonance frequncy 2
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Resonance frequncy 2
みなさん、こんにちは
再び共振周波数についての質問です。
添付ファイルを確認してください。
1. w2bとw4bの正しい周波数が見つからないのはなぜですか?
2. w2x(w2y)とw2a(w2c)は等しくありませんが、正しいですか?
また、w4x(w4y)およびw4a(w4c)。
3. R2 = 1mohm(1ohmではない)の場合、上記の2つの周波数は等しくなります。
さらに、それぞれw2とw4に等しくなります。
R1でこれが異なるのはなぜですか?
4.共振周波数は一般的に次のうちどれですか?
(1)最大/最小インピーダンス
(2)虚数部= 0(引数= 0)
これらのうち、3と4はMATHCADに関する質問ではありませんが、誰もが知っている場合はお知らせください。
Solved! Go to Solution.
- Labels:
-
Electrical_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I would like to second what Francesco wrote about using common nomenclature. I changed some of it in the attached worksheet.
According your solve blocks not finding the correct solution, the reason is the guess values. Those equations seem to be quite sensitive wrt guesses, Changing the guesses in the right direction makes the solve block work. Using a plot can help to find a suitable guess.
Hope the attached sheet helps
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ssato wrote:
Hello everyone
It is a question about the resonance frequency again.
Please check the attached file.
1. Why can't I find the correct frequency for w2b and w4b?
2. Is w2x (w2y) and w2a (w2c) not equal, but is it correct?
Also w4x (w4y) and w4a (w4c).
3. When R2 = 1mohm(not 1ohm), the above two frequencies are equal.
Furthermore, it becomes equal to w2 and w4 respectively.
Why is this different in R1?
4. Which of the following does the resonance frequency generally mean?
(1) Maximum / minimum impedance
(2) Imaginary part = 0 (argument = 0)
Of these, 3 and 4 are not questions about MATHCAD, but if anyone knows, please let me know.
OK.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi ssato,
I would like to suggest you to use the common way to write, with the use of MATHCAD, the units of measurement and the variables in Greek, IE: a microfarad is written 1 m control g F, that is 1μF; omega is written so: w CTRL g, that is ω.
Regards
FM
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I would like to second what Francesco wrote about using common nomenclature. I changed some of it in the attached worksheet.
According your solve blocks not finding the correct solution, the reason is the guess values. Those equations seem to be quite sensitive wrt guesses, Changing the guesses in the right direction makes the solve block work. Using a plot can help to find a suitable guess.
Hope the attached sheet helps
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner_E san
Thank you for your response.
However, does it mean that the position of the solution on the graph and
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner_E san
I wrote another one point in your attached file.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The one of Prime 5 by Werner_E of the WE_20190924_Resonance Frequency 2.xmcdz.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello ttokoro san
Thank you for your response.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
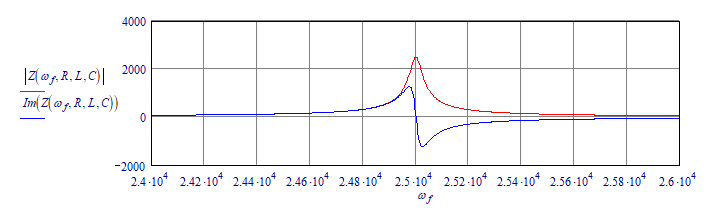
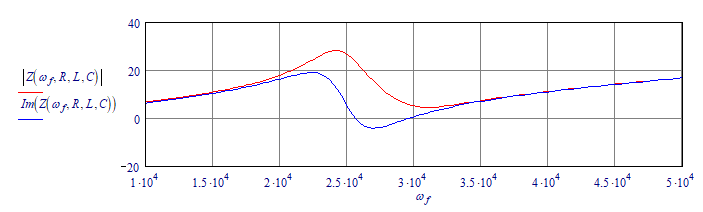
That is because resistors reduce the 'quality', or sharpness of a filter. With that they move the position of the extrema of the magnitude of the impedance.
A given filter with resistors at 10 mOhm:
The maximum of the magnitude of the impedance appears to coincide with the imaginary part being zero, at 25k. Now if I increase the resistors to 1 Ohm:
Notice that the single peak is split into two extrema; resistors are sometimes used for 'pole splitting'. The extrema of the magnitude of the impedance are below 25k and above 30k, while the zero's of the imaginary part are both between 25k and 30k.
If you plot the argument of the impedance along, you will find that its zero's coincide with those of the imaginary part. Argument=0 means there is no imaginary part, that is Im(Z)=0 as well. But the magnitude of the impedance is a mixture of the real and imaginary parts of the impedance. For some frequencies that may give a larger value than the real part alone.
For more info see: https://en.wikipedia.org/wiki/Resonance
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
こんにちはLucMeekesさん
あなたのコメントをよく理解しました。ありがとうございました。
---
しかし、インピーダンスの大きさは、インピーダンスの実数部と虚数部の混合です。
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ssato wrote:
Hello Werner_E san
Thank you for your response.
I understand that the guess value is important.I also understand that the estimated value is determined from the graph.
However, does it mean that the position of the solution on the graph andthe estimated value are not always the right or left?
The algorithm used by the solve block with "find" is Levenberg-Marquardt by default. You can change it by right-clicking on "find". You will notice that the other two alternatives (conjugate gradient and Quasi Newton) can't find a solution with your initial guess at all. As I understand it all three algorithms are some modification of the classic Newton.
This means that you can't tell which solution (if any) the algorithm will find for a specific guess value. Its sure not always to the left or to the right of it. Even with the simple classic Newton a guess value very close to a point of zero can converge at the end to another point of zero which is far away.
In case of your original file the algorithm was converging in the "wrong" direction and stopped at the limit you had set.
According your confusion about resonance frequency - you have to distinguish between two of them (I am not sure about the correct English names) !
1) phase resonance: this is usually meant when you read resonance and means that the imaginary part has to be zero
2) amplitude resonance (magnitude resonance ?): This is where the magnitude has local extreme.
Phase and amplitude resonance frequency must not be the same and this is what you experience in your sheet.
BTW, ttokoro is absolute right when he mentioned in he sheet that the unit of omega should not be written in Hz but rather s^-1 or even better rad/s.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner_E san
Thank you for your comment.
I use MATHCAD's SOLVE BLOCK with attention to your comments.
Also, I agree the TWO resonance frequency and the unit of ω.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems that in case of your equations the use of the "root" command is more reliable than the solve block which is quite sensible with respect to the guess value.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner_E san
I will use ROOT command. Thank you.