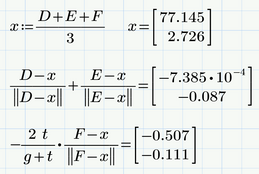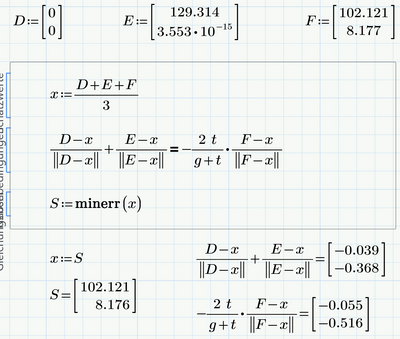Root finding of vector function using find

[FP_10119833]

Hello everyone

I have been a bit puzzled by the error I get when using find with vector variables. I have defined a triangle DEF in 2 dimensions. I am searching for the coordinates of a 4th point S such that the sum of vectors from S to the other points is a zero vector (weighed with parameters g and t). Unfortunately, find does not find a solution.

I thought maybe it was due to a divide by zero error, but adding the constraint that the product of the norms must be strictly positive does not solve the problem. The initial guess is already fairly close to the solution, so I don't believe it is the issue.

I have attached the mcdx file as well as a screenshot for convenience. Any idea of what is going wrong ?

 

François

[VladimirN]

One of the possible solutions in the attachment.

[Werner_E]

The x= mean of the three points wasn't meant as an additional condition but was the guess value! 🙂

[VladimirN]

I slightly changed the conditions of the problem and used it as an example 🙂.

[Werner_E · Accepted solution]

---

The initial guess is already fairly close to the solution

I wouldn't call that "close":

I don't think that your equation has solution!

I am not sure about the properties you demand for your points S and suggest that you check your equation.

Using "minerr" gives us a  "solution" very close to point F but there seems to be no solution which fulfills the equation to 100%

[FP_10119833]

Thank you Werner and Vladimir for suggesting the use of minerr.

Since S has to be inside the triangle DEF, using the centroid seems a good enough guess without further info. That's what I meant by fairly close. In fact Werner's suspicion is correct that the problem simply has no solution with the proposed set of parameters g, t. For instance, changing g from 200 to 400 does work. That will teach me about trying to validate a program with no physical solutions ! 😅

I will try to improve the sheet so that it correctly returns no solution, rather than the error. There again minerr seem to come handy.

Thank you for the swift support !

[VladimirN]

You're welcome.

[Werner_E]

---

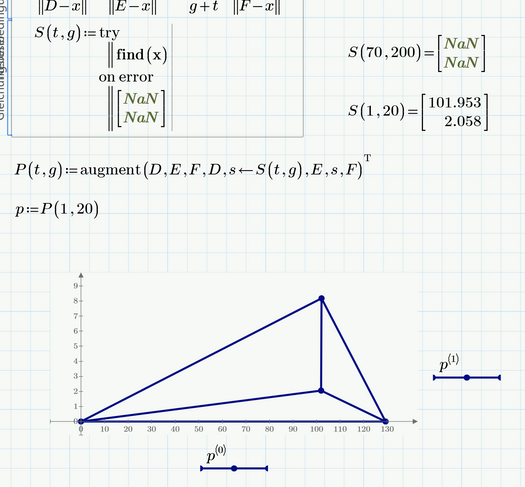
For instance, changing g from 200 to 400 does work.

Yes, there is only a solution if the ratio g:t is greater than 4.393 (with this ratio you get S=F).

---

I will try to improve the sheet so that it correctly returns no solution, rather than the error.

---

You could turn the solve block into a function dependent on t and g and check for the existence of a solution using "try ..on error...".

With a small modification you may also plot a graphical representation