Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Second task with 3 masses not with strings - with springs
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Second task with 3 masses not with strings - with springs
It is continue of One task with 3 bobs - Forces searching
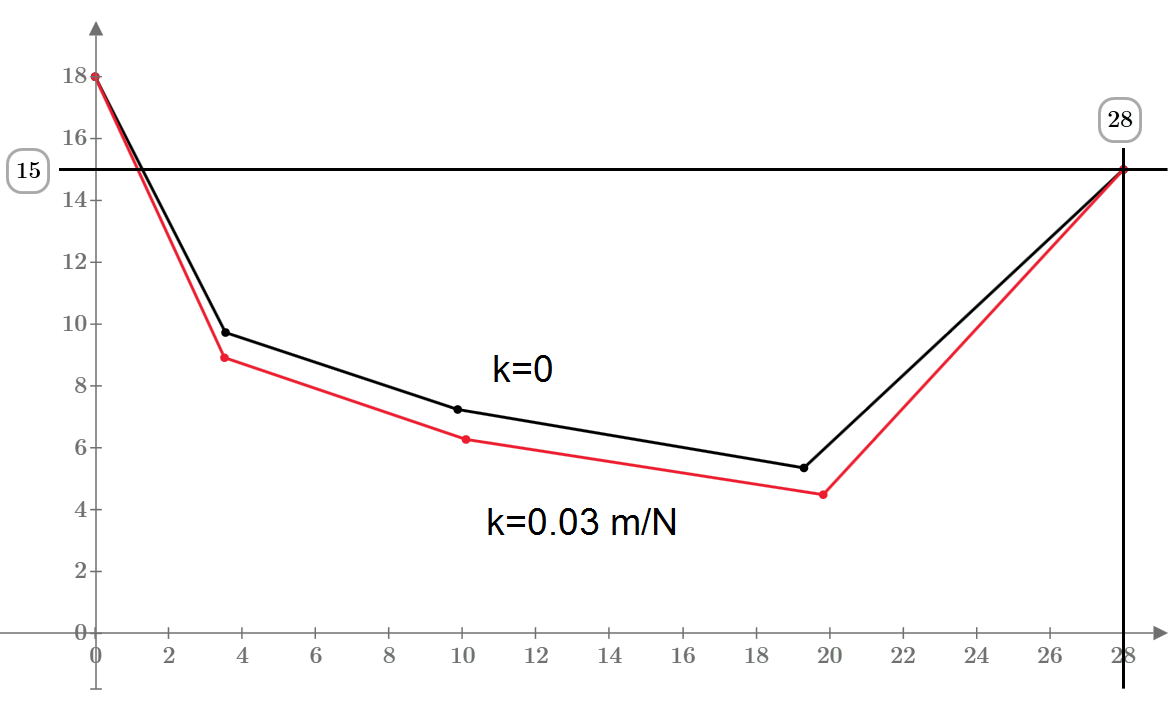
But we have not strings (k=0 m/N) but springers (k>0 m/N)
I have solved this new task with using forces analyze - see the picture and the sheet Prime 3.1 in attach.
Is it possible to solve this task by using the Lagrange method - with energy (potential and/or strings energy) minimization (see please the first task)?
Thank you!
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Утро вечера мудренее! It is old Russian proverb!
Sheets with Minimize (Lagrange) and with Find (Newton) have same result! Ура!
See please attach
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One more try in attach.
With values in result. But is this values correct?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If we set k to a value of 10^-10m/N (a very stiff spring with a stiffness near to a string without springs) we should expect results of the former problem we have solved correctly:

compare my worksheet in attach please.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Volker Lehner написал(а):
If we set k to a value of 10^-10m/N (a very stiff spring with a stiffness near to a string without springs) we should expect results of the former problem we have solved correctly:
compare my worksheet in attach please.
Yes, SE=0 and we have the former task! With x and y not with F ???
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think it's a numerical problem, look here and compare:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Утро вечера мудренее! It is old Russian proverb!
Sheets with Minimize (Lagrange) and with Find (Newton) have same result! Ура!
See please attach
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
...кропотливо белка ест ...A German proverb for industrious.
I changed the spring stiffness in both (Find and Lagrangesche) to 10^-6m/N and have different results.
Both Modells have completely the same spring stiffness but different results.
Numerical property.
By setting the stiffness to all for 0.03m/N we have same results again.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have added in the article:
На сайте Solved: Re: Second task with 3 masses not with strings - w... - PTC Community размешено решение несколько усложненной задачи о провисающих грузиках, где жесткие нити заменены на невесомые пружины с разным коэффициентом упругости на разных участках. Применен и метод Ньютона (анализ баланса сил – 10 уравнений) и метод Лагранжа (минимизация энергии – 4 уравнения). Энергия же в этом случае представляет собой сумму (f) потенциальных энергий грузиков (PE) и потенциальной энергии пружин (SE) – см. рис. 28. Два расчета дали одинаковые результаты, но метод Лагранжа оказался намного проще в реализации. На сайте статьи можно найти анимацию колебания грузиков, когда жесткая нить мгновенно заменяется на пружины. Система при этом переходит из одного стабильного состояния в другое, выделывая разные па.
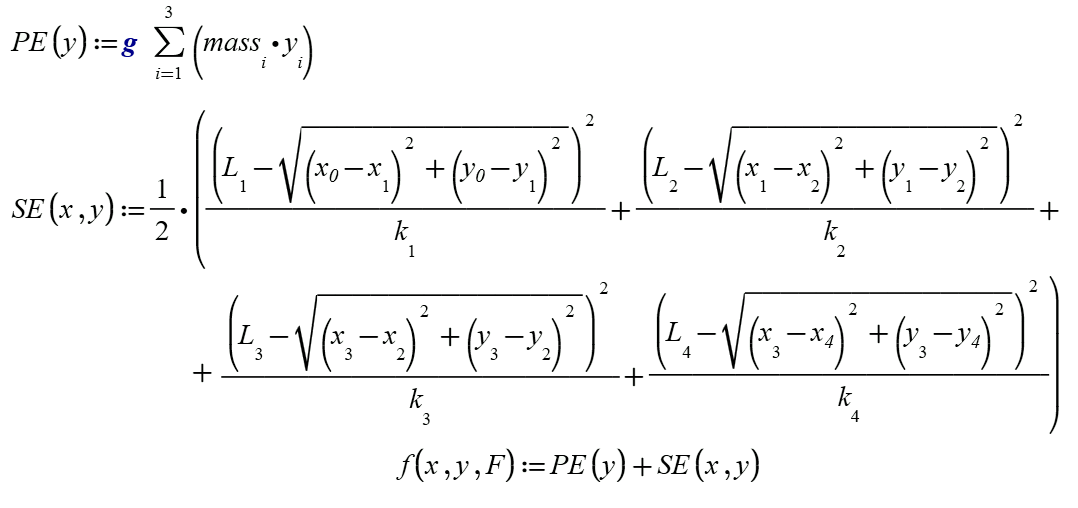
Рис. 28. Энергии грузиков на пружинах (k – величина, обратная коэффициенту упругости пружины)
Но при уменьшении значений коэффициента k с 0.03 до, например, 0.000001 разница в результатах работы метода Ньютона и метод Лагранжа становится заметной, что можно объяснить особенностям численного (приближенного) решения задач.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
...next task...:
Let's do it with an increasing mass like he did-for a pendulum:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Volker Lehner написал(а):
...next task...:
Let's do it with an increasing mass like he did-for a pendulum:
Increasing mass:
See please pictures (and text) here http://twt.mpei.ac.ru/ochkov/Rocket.pdf
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ValeryOchkov написал(а):
Утро вечера мудренее! It is old Russian proverb!
In German: Über Nacht kommt guter Rat.
Немецкие пословицы с переводом | Немецкий язык онлайн. Изучение, уроки.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov schrieb:
In German: Über Nacht kommt guter Rat.
oder: "Gut Ding braucht Weile" - a good old german saying.






