Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Simultaneous equations not solving MathCad 15
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Simultaneous equations not solving MathCad 15
I have started a worksheet that will calculate many simultaneous equations at the same time. I have set everything up and all of my units work out when checked individually, but when I set the equations up to solve all at the same time then I am receiving an error claiming that my units are incorrect. I have attached the file for help. When I trace error it comes with saying that the problem exists with solving for "Q".
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Have a look at the attached. I am not sure on the results and the equations as the solve block returns different answer for different guess values. However, it does converge to a solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
First error I found.
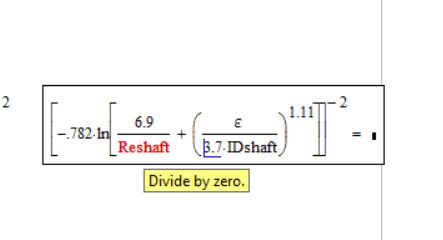
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I had originally had it guessed at 2000 because that is a good estimate for turbulent flow, but was playing around with different guess values earlier and saved it at 0 before I changed it back. I have since then changed it back to 2000 and still have the same error.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Have a look at my sheet below.
Please note I removed the gravity constant from following equation as the units did not match.
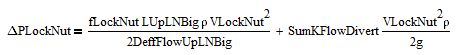
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Have a look at the attached. I am not sure on the results and the equations as the solve block returns different answer for different guess values. However, it does converge to a solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you! Do you know of a way make the the solutions not look into negatives? In other programs that I have worked in I am able to go in and say that the solution range is between 0 and infinity vs negative infinity to infinity.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You can place the statement "fshaft>0" somewhere in the solve block, but you will notice that it looks like it gets ignored. It treated like a soft constraint, so you can "weight" it by typing something like "fshaft*100>0" and that works.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am still working on this, but running into a small issue. I have added an additional section to the problem and have continued. to run it. However, my guess values seem to have a major impact on the solution. This bothers me because there should not be multiple solutions to the problem. The biggest thing that is bothering me is that I cannot get the Q's to add up right. Q should equal Qbrg plus Qshaft, but they are obviously different. It seems like the program is ignoring the statements like Werner suggested they would. The Delta P's always seem to add up correctly, but not the Q's. Any thoughts?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I wonder if you really need to solve for 14 variables at the same time.
Some remarks.
Its not necessary to add Q=90gpm as a constraint. Q is already a variable with that value and will not change anyway.
Constraints are soft constraints and Mathcad tries to minimize the overall error and so constraints are treated as soft constraints.
Weighting of constraints: I have shown how to weigth a constraint like x>0.
If Mathcad ends upt with x=-0.2, the absolute error for this constraint is possibly 0.2.
If you write x*1000>0 and x=-0.2, the error is 200 and chances are Mathcad will try to do better (at the expense of other constraints and equations).
I see you have something like x*100000<0.1. Are you sure this is what you mean? It means that x should be smaller than 10^(-6). If you want x<0.1 and you want to weight it, you should rather use something like 100000*(0.1-x)>0.
Sam Collette wrote:
However, my guess values seem to have a major impact on the solution. This bothers me because there should not be multiple solutions to the problem.
Hmm, you have 14 variables, 14 equations and some less than 20 additional constraints. I don't think there is a unique solution at all but quite a lot of "best fits" and depending on how the problem is conditioned guess values sure may play a big role.
The biggest thing that is bothering me is that I cannot get the Q's to add up right. Q should equal Qbrg plus Qshaft, but they are obviously different.
If thats so important, you may weight that equation higher than the rest: (Q-Qbrg-Qshaft)*10^6=0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you, Werner. That did the trick on this step. Unfortunately, I am sure that I may run into some additional issues as I move forward with this. I expect to get to around 60 simultaneous equations by the time it is all said and done with this particular problem. The next one that I evaluate looks to be around 100 or more simultaneous equations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Seems to me you only need to solve for the three velocities. Everything else can be obtained as a function of these. See attached.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Great Alan, waht a difference!
Thumbs up!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I should have noted that the pressure drop function I defined represents the friction loss only. To get the displayed pressures in the results to sum to the overall shaft pressure drop you need to add in the shock loss terms.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alan,
You are right that I am really interested in the Velocities. I set up the equations the way that I did because that was how I was taught to do it when I learned how to solve flow problems and that was how the book that I was looking at had similar problems set up. I think that your method is much cleaner than mine was. I am going to try to run with your method and see where I can get with it. I have another 4 or 5 components to add in.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, all you really need within the solve block are Kirchoff's laws (sum of flows into a node is zero; pressure drop between any two nodes is independent of path taken); pretty much everything else can be expressed as a function outside the solve block.
Alan





