Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solve Block Error!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve Block Error!
Mathcad is returning an error saying that no solution was found for a variable and I can't understand why ![]() It's a variable that already has a set value.
It's a variable that already has a set value.
I hope someone here can please see why this is happening! The start of the solve block is about 3/4 of the way down the sheet, starting under the heading 'Guess Values', ignore the other stuff.
I realise the variable names are long and annoying sorry.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A solve block never returns an error saying no solution was found for a specific variable, Actually, in MC12 and later a solve block never returns any error other that the useless "this variable is undefined", but if it did return a valid error it would be simply that it can't find a solution.
Anyway, the first thing you need to do is get rid of all the unnecessary equations in the solve block. For example, you have naphos=naphos6, and you do not solve for naphos. So above the solve block just assign naphos6:=naphos. You also have naphos7=naphos6, so you can get rid of that too. And you have naphos=nahos7, which, given the other two equations, is not an independent equation and should not be there. There are many more like these.
Once you have done that for all the variables that are equal, it would be a good idea to pick one variable name for each, and substitute that into all the remaining equations. Then check whether that leaves you with more redundant or non-independent equations that can be eliminated. The more you can simplify the solve block, the easier it will be to find the real problem. Right now, with all those variables with multiple names and non-independent equations in there, it would be almost impossible. it's not even possible to know if the number of equations you have actually matches the number of unknowns you are solving for.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That actually fixed it! Thanks so much ![]() I initially meant that when i traced the error, it lead to a variable and said no solution was found for it.
I initially meant that when i traced the error, it lead to a variable and said no solution was found for it.
Thanks again!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That actually fixed it! Thanks so much

I didn't expect that! I just thought it would be the first step to finding the problem. I love it when things work out to be easier than expected ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems I spoke too soon actually ![]() I noticed that I had accidentally kept the equivalent variables in the 'Find' part of the solve block and it found a value for naphos6 different to naphos even though before the solve block i said naphos6:=naphos, so I took out all the equivalent variables and the error has re-appeared. Here is the same sheet with the changes.
I noticed that I had accidentally kept the equivalent variables in the 'Find' part of the solve block and it found a value for naphos6 different to naphos even though before the solve block i said naphos6:=naphos, so I took out all the equivalent variables and the error has re-appeared. Here is the same sheet with the changes.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To the right of the "Given" you have a group of equations that is partially (in fact mostly) within the solve block (the ones ending in BA4=BA7+BA8). Move them out of the solve block.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That worked, thanks again! ![]() I have added another similar solve block and it is returning an error again, would you please have a look again? It starts under the heading 'Back Extraction'.
I have added another similar solve block and it is returning an error again, would you please have a look again? It starts under the heading 'Back Extraction'.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have 26 equations, you are solving for 25 unknowns. For Find, the number of equations must match the number of unknowns.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I managed to compile two of the equations together to make 25 equations altogether and it worked, thanks! ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
You have 26 equations, you are solving for 25 unknowns. For Find, the number of equations must match the number of unknowns.
Not allways - see the problem with 7 equations and 6 unknowns
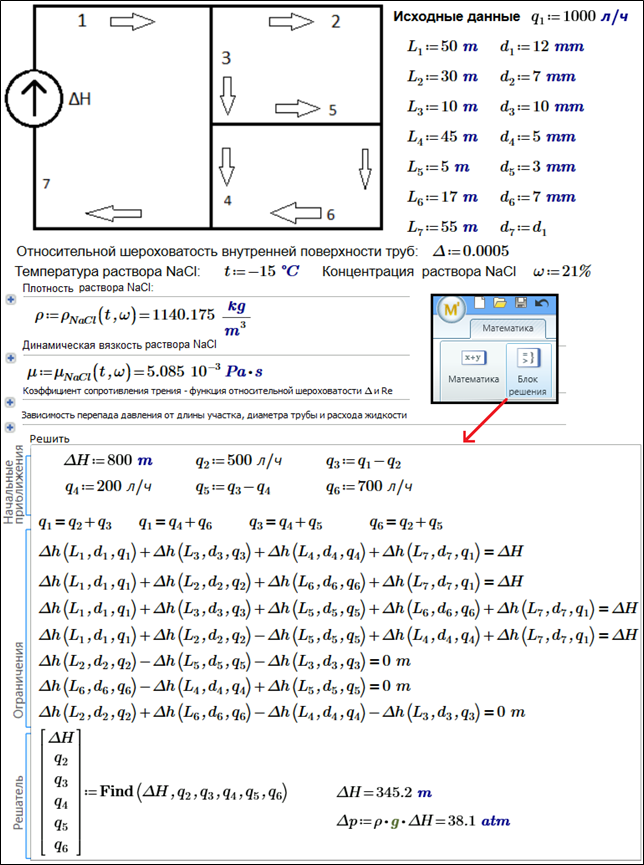
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So your equations are not all independent. Does the solver in Prime always always let you get away with that, or did you just get lucky in thins one case?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
So your equations are not all independent.
Sorry I have read: "the number of equations must match the number of unknowns" not "the number of independent equations must match the number of unknowns" ![]()
Richard Jackson wrote:
Does the solver in Prime always always let you get away with that, or did you just get lucky in thins one case?
My answer on your new question is old: "Not allways".
Second case - the number of unknowns > the number of [independent] [nonlinear] equations
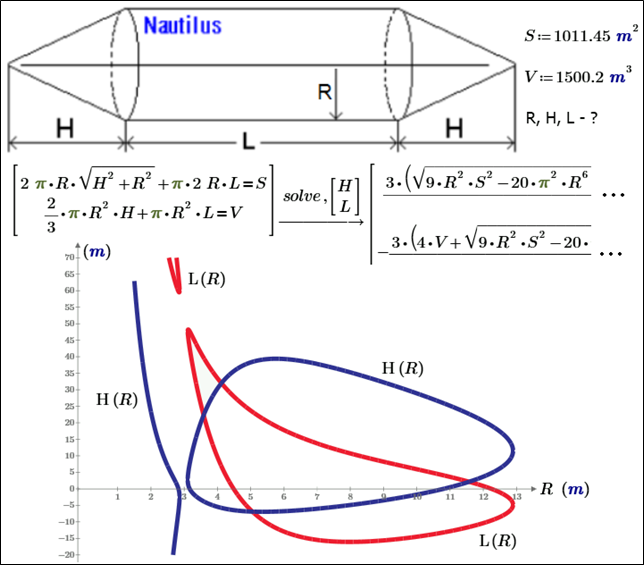
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I ended up having to change a few values at the start and add in another component to the balance. The equations all seem correct to me and i have neatened up the solve block showing all the variables. It is returning an error again and I was wondering if you could have a look again please. I have 42 guess values and 44 equations but I can't see any equations that are redundant ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You have 44 equations and only 42 unknowns to solve for, so your system of equations is overdetermined. You either need to eliminate two equations (which of course may then not be satifiied using the values of the variables you do solve for), or you need to treat two more variables as unknowns, and allow them to vary.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The only thing i can think of doing is substituting the BA6 = 0.006847*water6 and BA7 = 0.006847*water7 variables into the equations containing them. This brings the number of equations down to 42 but still returns an error.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You should do that. Also for BA8 and BA5. However, when you have done that although you have eliminated four equations you have also eliminated four unknowns (BA5, BA6, BA7, and BA8). So you you still have the same problem. If you have more independent equations than you have unknowns, then there is most likely no solution.





