Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Solve Block Issue - Improvement Required
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve Block Issue - Improvement Required
I have a spreadsheet which calculates the reaction, deflection and slope of a HDPE pipeline as it is being flooded to the seabed for a given water depth. There is 7 no. simultaneous equations which have to be solved in order to obtain the results.
My issue is that the solve block is very sensitive to the guess values, and I often find myself tweaking them until the solve block returns a solution which can be extremely tedious. - Changing Ra to 50 in this instance.
So my question is, can this method be improved and could the equations be solved symbolically?
Cheers,
Mike
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think if the last equation in your solve block is replaced by one in which moments are taken about B instead of A you will have your last independent equation. I think it will be: w1*L1^2/2 + w2*L2^2/2 - Ra*L1 - Rc*L2 = 0
This gives a robust solution (though, since I don't know what the physical scenario is actually like, my equation might well be wrong!).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have same problem (the solve block is very sensitive to the guess values) with my system 10 equations.
New input data and now solution ![]()
My solution of this problem.
When I have a solution of the system I copy it as a guess value.
Than I "little" change input data and copy and paste again.
If I have no solution I do a little step back.
We can do it only in Prime if we have different units in answer:
In Prime

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
I have same problem (the solve block is very sensitive to the guess values) with my system 10 equations.
New input data and now solution
My solution of this problem.
When I have a solution of the system I copy it as a guess value.
Than I "little" change input data and copy and paste again.
Again, I can imagine this being time consuming and cumbersome. I was hoping to get an automated solution or symbolic solution which will not rely on initial guess values.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike Armstrong wrote:
I was hoping to get an automated solution
Use the Newton method
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There's no way you can get s symbolic solution. Your equations are a set of high order polynomials in your unknowns. You can eliminate L1 and L2, to reduce the number of equations, but when you do that it shows up a problem. It seems one of your equations is not independent. Unless I made a mistake, anyway, so you had better check what I did carefully.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Update:
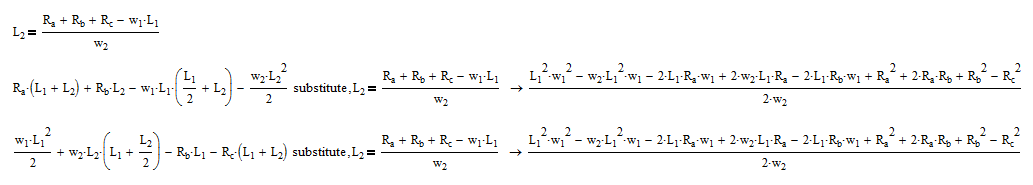
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Even with the update, there still seems to be an error with EQ5.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm not sure what you mean. The update just confirms what I and Andy have previously said. Your equations for the bending moments at A and C and the equilibrium relationship are not independent.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Right I get it, well sort of.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If I substitute the equation for the equilibrium relationship into the equations for the two bending moments I get the same expression. So the three equations are not independent. You need to either get rid of one equation. and fix one of the variables you are currently solving for, or find another independent equation to replace one of those three.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Mike,
I'm not sure, but do you have 7 independent equations?
I've read through the attached & I can't see an obvious error.
looks like equations 5 & 7 can be manipulated to give equation 6.
Hope this helps
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A Westerman wrote:
Hi Mike,
I'm not sure, but do you have 7 independent equations?
I've read through the attached & I can't see an obvious error.
looks like equations 5 & 7 can be manipulated to give equation 6.
Hope this helps
Andy
Hi Alan,
I believe I do have 7 independent equations, but unsure why it cannot be solved symbolically. Still digesting Richards sheet ![]()
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The last three equations within the solve block are linear in Ra, Rb and Rc and can be solved symbolically to find them in terms of L1 and L2. If you do this you find Rc is identically zero. You can therefore reduce your number of equations/unknowns to 6, but this still doesn't help. You can further reduce the number of equations to 2 (for L1 and L2) by defining thetab and deltab as functions of L1 and L2 (making use of Ra and Rb, also defined as functions). You then have two equations/unknowns (L1 and L2), but this still doesn't really help! Are you sure you have all your signs correct?
Alan.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The reason you find Rc to be zero is because the last three equations are not independent, and therefore cannot be solved to find three variables.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
The reason you find Rc to be zero is because the last three equations are not independent, and therefore cannot be solved to find three variables.
Yes, I should perhaps have noted that that is the implication.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
The reason you find Rc to be zero is because the last three equations are not independent, and therefore cannot be solved to find three variables.
Thanks for the help Richard. I will try and get to the bottom of it when I have access to Mathcad.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry for the delayed response, Mathcad on my home machine is no longer working.
AlanStevens wrote:
The last three equations within the solve block are linear in Ra, Rb and Rc and can be solved symbolically to find them in terms of L1 and L2. If you do this you find Rc is identically zero. You can therefore reduce your number of equations/unknowns to 6, but this still doesn't help. You can further reduce the number of equations to 2 (for L1 and L2) by defining thetab and deltab as functions of L1 and L2 (making use of Ra and Rb, also defined as functions). You then have two equations/unknowns (L1 and L2), but this still doesn't really help!
Thanks for the detailed response, but I am unable to attempt this until tomorrow.
Are you sure you have all your signs correct?
I have to admit that the worksheet was not written by me and is part of a 'historical' spreadsheet my company uses. I believe the signs are correct as the deflection and slope graphs in the attached sheet visually look correct.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's my analysis using symbolics (Mathcad 11, probably will not work in 15 as the assignment of symbolic results to variables is not supported anymore). The conclusion is that you're lacking one (independent) equation involving L1 and L2.
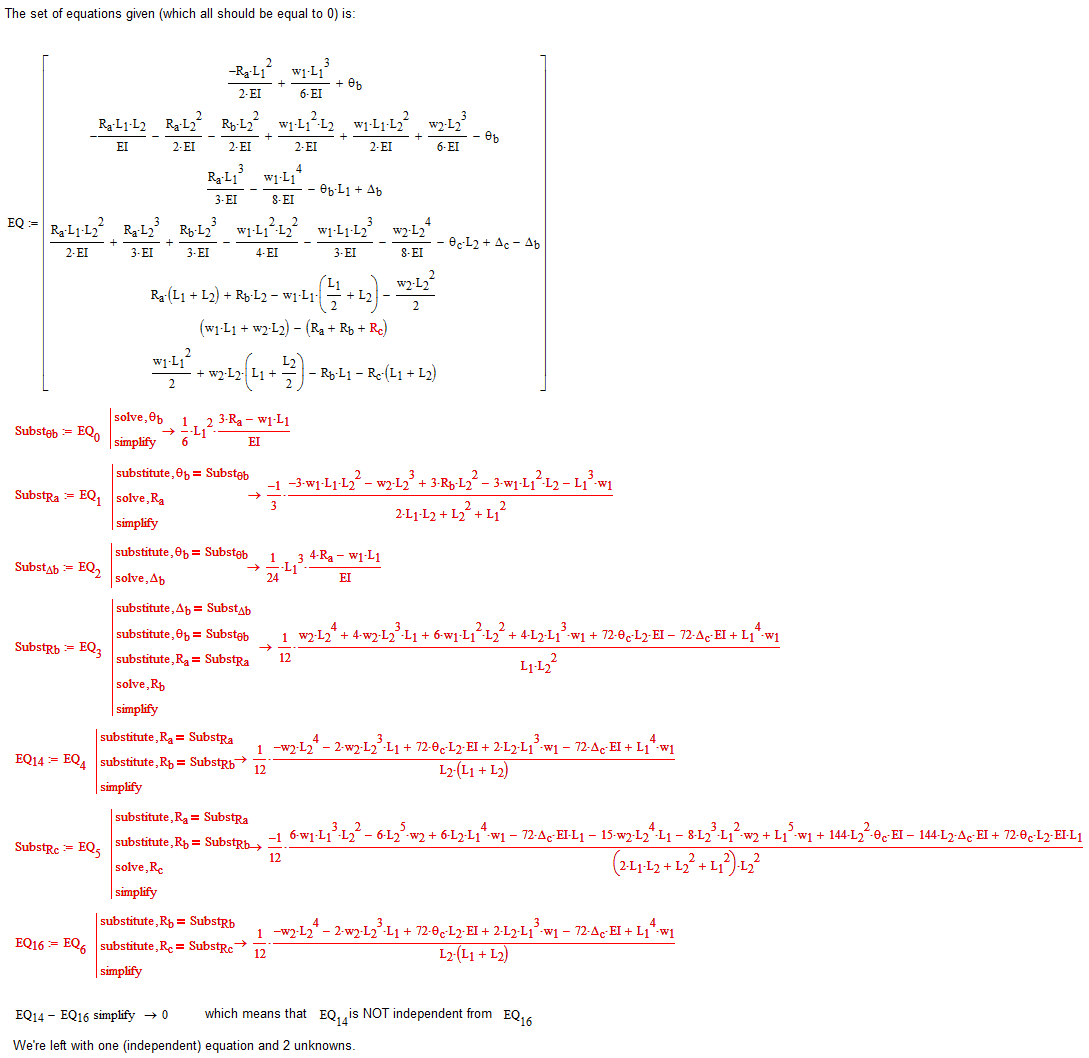
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Superb work Luc. I am a little stuck in terms of advancing this now. As I said earlier, I inherited the worksheet and did not write it myself. Maybe it is time to start again with it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike,
If you have (access to) the knowledge to revisit the model, go ahead. You can do most of the symbolics also in M15, but you have to write out the substitutions. My first two lines would be like:

etcetera. Tedious copy and paste work, but it can be done.
Did the original author of the sheet ever provide a solution for the 7 unknowns based on this set of equations? Now is the time to question that work and whatever it has lead to! (I don't know the background, but there might be risks involved...?)
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes wrote:
Mike,
If you have (access to) the knowledge to revisit the model, go ahead. You can do most of the symbolics also in M15, but you have to write out the substitutions. My first two lines would be like:
etcetera. Tedious copy and paste work, but it can be done.
Thanks Luc. This is similar to advice Richard, Andy and Alan provided. My symbolic skills are relatively poor compared to my other average Mathcad capabilities ![]()
Did the original author of the sheet ever provide a solution for the 7 unknowns based on this set of equations? Now is the time to question that work and whatever it has lead to! (I don't know the background, but there might be risks involved...?)
Success!
Luc
Worryingly, these set for formulae have been used, and unquestioned for many year. The built in FOS in the allowable stresses probably mitigated the risks. However, I would like to get to the bottom of it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I know next to nothing about this subject, but if the pipielines didn't fail when being laid it doesn't seem very likely to me that they would fail in the future.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I know next to nothing about this subject, but if the pipielines didn't fail when being laid it doesn't seem very likely to me that they would fail in the future.
Quite true. However, there is obviously something wrong with the formulae which has only come to light from feedback in here. I think it will be a small discrepancy in BM equations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mike Armstrong wrote:
I know next to nothing about this subject, but if the pipielines didn't fail when being laid it doesn't seem very likely to me that they would fail in the future.
Quite true. However, there is obviously something wrong with the formulae which has only come to light from feedback in here. I think it will be a small discrepancy in BM equations.
The Safety Engineer in me is cowering under the table pleading with people to "Have The Bad Man Stop Saying Things Like That".
The Tabloid Editor, Ambulance Chaser and Vicarious Disaster Watcher in me are grinning in anticipation - The Emperor Murphy's ears are probably twitching at this very moment. ![]()
Seriously, Mike's company has probably got one of these Ethics Policy things that will require him to flag it up as a problem (gone are the good old days of a plain old "Nah, it'll be all right"). The corollary of this will be a documented rationale for why it'll be alright, which means he (or someone else) will probably have to investigate it anyway to at least bound the likely errors.
I always try to keep in mind that accidents are usually the result of a chain of things going wrong rather than just one thing going wrong; so the solution to the equations could be fine, but sufficiently out that the systems strays into trouble elsewhere. I also try to keep in mind the "unusual circumstance" scenario - I once discovered a fault in a comms system that would have taken out most of the system in one exact scenario, which was very unlikely to occur in peacetime but almost certain to happen in wartime and just when you didn't need it to happen (I don't know how long Murphy had been planning that one, but he's had a downer on me every since I found it).
Do you think you could possibly please endorse me for my Teaching Grandmother To Suck Eggs skills? ![]()
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
![]()
![]()
![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Look up "Therac-25" on Wikipedia. Sometimes assuming everything will work OK is not good enough!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
Look up "Therac-25" on Wikipedia. Sometimes assuming everything will work OK is not good enough!
"AECL had never tested the Therac-25 with the combination of software and hardware until it was assembled at the hospital." Murphy must have patted himself on the back and taken the week off after that one.
---- I was involved with a Major System where they were planning to put Major Safety System 1 (we're talking Major Headlines here if it went wrongl) and Major Safety System 2 on a distributed processor network. To save costs Subcontractor A were going to develop and test MSS1 at their site, Subcontractor B were going to develop MSS2 at their site and integration testing would done during acceptance ... I'm still cowering under the table about that one and I'm not a safety engineer.
""A naive assumption is often made that reusing software or using commercial off-the-shelf software will increase safety because the software will have been exercised extensively." Gotta agree with that one - I often find that software hasn't extensively exercised many of the features that I tend to want to use ... and I often get the blame for using them!
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
StuartBruff wrote:
Do you think you could possibly please endorse me for my Teaching Grandmother To **** Eggs skills?
... One of these days, every word in the English Language is going to be so overloaded with scatological and other meanings that the spell checker will turn entire documents into a string of censored expletives. It never even crossed my mind that Granny would s-u-c-k anything but eggs, and I had to spend a minute or so wondering why the 4 asterisks as I was pretty sure I hadn't typed an "f" by mistake (although with my new laptop's trackpad, I wouldn't entirely dismiss that scenario, as the cursor jumps all over the place when my hands are closer than an inch or so away. Why can't they put trackpads out of the way of the palms?).
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think if the last equation in your solve block is replaced by one in which moments are taken about B instead of A you will have your last independent equation. I think it will be: w1*L1^2/2 + w2*L2^2/2 - Ra*L1 - Rc*L2 = 0
This gives a robust solution (though, since I don't know what the physical scenario is actually like, my equation might well be wrong!).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
I think if the last equation in your solve block is replaced by one in which moments are taken about B instead of A you will have your last independent equation. I think it will be: w1*L1^2/2 + w2*L2^2/2 - Ra*L1 - Rc*L2 = 0
This gives a robust solution (though, since I don't know what the physical scenario is actually like, my equation might well be wrong!).
Alan
This seems to be the solution. I have just swapped the equations out and the graphs look good and do not change when the guess values change. Superb work.
However, when I solve symbolically I am not getting the same reaction forces as the numerical solution, which doesn't seem correct.